Academic Modules Analytic and Solid Geometry
1st Semester S.Y. 2024-2025
Introduction
Plane analytic geometry, also known as coordinate geometry, combines algebra and
geometry to study geometric figures using a coordinate system.
Plane analytic geometry is used in various fields such as physics, engineering,
computer graphics, and more. It helps in solving geometric problems algebraically
and visualizing geometric relationships.
Understanding these fundamentals will give you a solid foundation in plane analytic
MODULE 1 geometry, helping you to analyze and solve various geometric problems
systematically.
In this modules you will study the basic key concepts: Cartesian coordinate system,
distance formula, slope of a line, division of a line segment, midpoint formula,
parallel and perpendicular lines.
PLANE ANALYTIC GEOMETRY Learning Outcomes
After completing this module students must be able to:
1. Understand the structure of the coordinate plane, including x – axis, y –
axis, origin and quadrants.
2. Plot points and interpret their coordinates on the plane.
3. Calculate the distance between two points using distance formula and
midpoint formula.
4. Understand the meaning of slope in terms of line steepness and direction.
References:
1. Gabuyo, Y. (2013). Analytic Geometry. Rex Book Store.
2. Felipe L. C. Jr. (2009) Analytic Geometry Made Easy
Instructor : Engr. Ma. Clarissa Ramos-Cortez
Academic Modules Analytic and Solid Geometry
1st Semester S.Y. 2024-2025
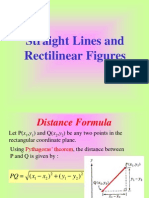
I. PLANE ANALYTIC GEOMETRY 1.2 Distance Formula
Consider two points whose coordinates are (x1 , y1 ) and(x2 , y2 ), respectively. A
Introduction
right triangle is forms with the distance between two points being the
Analytic Geometry is a branch of geometry that deals with geometric problem using hypotenuse of the triangle.
coordinate system and transforming them into algebraic problems.
It was Rene Descartes (1596 1596 – 1650), a French philosopher and
mathematician, who developed the unification of geometry and algebra. He
developed the idea of investigating curves by means of algebraic methods.
1.1 Cartesian Coordinate System
A number line is directed line with its points corresponding to real numbers.
The number corresponding to a point is called coordinate of a point. (+. -)
Horizontal number line is also known as x-axis.
Vertical number line is also known as y-axis.
The intersection between x and y axes represent the point of origin
(0,0).
Cartesian coordinate system or rectangular coordinate system, a system Example 1: Distance Formula
used to graph point or set of points. Find the distance of the line segment connecting the points A (6,4) and
Each point P(x,y) in a plane has one-to-one correspondence where the B (2,8).
domain x and y is the set of real numbers. P(x,y) is called an ordered pair. Example 2: Distance Formula
The first number in the ordered pair is x-coordinate or abscissa, Find the distance between A (4, -3) and B (-2, 5)
which represents the horizontal distance of a point from y-axis. Example 3: Distance Formula
The second number in the ordered pair y-coordinate or ordinate, If the distance between points (3, y) and (8, 7) is 13, find y.
which represents the vertical distance from x-axis. Example 4: Distance Formula
Find the coordinates of a point equidistant from (1, -6), (5, -6) and (6, -1).
1.3 Point-of-Division Formulas
Consider two points with coordinates (x1 , y1 ) and(x 2 , y2 ). The line segment formed
by these two points is divided by a point P whose coordinates are (x, y).
If the point, M is at the midpoint of the line
segment, then the abscissa and ordinate of
the point are the following:
Instructor : Engr. Ma. Clarissa Ramos-Cortez
Academic Modules Analytic and Solid Geometry
1st Semester S.Y. 2024-2025
1.4 Slope of a Line (gradient) 1.6 Angle from One line to Another
The slope of a line is a number that measures its “steepness” and it is usually
denoted by the letter m.
Consider two lines (line CPD and line APB)
with slopes of m1 and m2 .
The angle ∅ between these lines (line CPD
and line APB) may be calculated using the
formula:
SAMPLE PROBLEMS:
1.5 Parallel and Perpendicular Lines
A line parallel to the x-axis has a slope of zero while a line parallel to the y- 1. Draw the figure on coordinate paper, choosing a suitable scale in each instance:
axis has a slope of infinity. a) Triangle with vertices (0,3), (-1, -2) and (4,1). b) Quadrilateral with vertices (-
For parallel lines with a slopes of m1 and m2 , respectively, the slope are the 1,2), (-1, -1), (3, -4) and (5,4).
same. (m1 = m2 )
For the perpendicular lines with slopes of m1 and m2 , respectively, the slope 2. Find the distance between the given points (2,1) and (5,5).
1
of one is the negative reciprocal of the other. (m2 = − 𝑚 )
1 3. Show that the points (1,4), (7,0), (5, -3), (-1,1) are the vertices of a rectangle, and
Distance between two Parallel Lines find its area.
Consider two parallel lines with equations as shown in the figure.
Use the sign (either + or -) that would make the distance positive. 4. Find the point midway between the given points (5,6), (3, -2).
5. Find the slope of the line joining the given points (6,2), (3, -4).
6. Find the angle between two lines (2,0)(3,5) : (5,2)(4,6).
7. Find the area of the triangle with vertices (2, -5) (6,2) (4,1).
8. Find the angle from the first line to the second. 2x+3y=0; 7x-y=4.
Instructor : Engr. Ma. Clarissa Ramos-Cortez