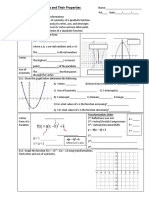
Graphing a Quadratic Function: 𝒇(𝒙) = 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄
Quadratic Functions are second degree polynomials (i.e. highest power of the domain variable is 2).
Quadratics can be written in several forms - General Form, Standard Form (also called Vertex Form), and
Factored form*. The graph of a Quadratic Function is called a Parabola. It’s general shape is curved and looks
like a “U”. The “U” is right side up if “a” is positive (𝑎 > 0) , and it is upside down if “a” is negative (𝑎 < 0).
The Vertex (h, k) is either the lowest (right side up) or the highest (upside down) point on the parabola. The
Axis of Symmetry is a vertical line that visually cuts the parabola in half and is written as 𝑥 = ℎ.
General Form (𝑎, 𝑏, 𝑐 ∈ ℝ ) Standard (Vertex) Form (𝑎, ℎ, 𝑘 ∈ ℝ )
𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 𝑓(𝑥) = 𝑎(𝑥 − ℎ)2 + 𝑘
The y-intercept (0, 𝑐) of the graph is easily The Vertex (ℎ, 𝑘),
identifiable from General Form. The Min/Max value (𝑘) of the function, and
The Axis of Symmetry (𝑥 = ℎ)
The x-intercept(s) (if any) can be found by factoring
and/or using the quadratic formula. are all easily identifiable from Vertex Form.
−𝑏 ± √𝑏 2 − 4𝑎𝑐 The x-intercept(s) (if any) can be found by using the
𝑥=
2𝑎 square root property.
The Vertex (ℎ, 𝑘), Min/Max value (𝑘), and Axis of The y-intercept can be found by evaluating 𝑓(0).
Symmetry (𝑥 = ℎ) can be found by completing the
square or by using the vertex formula: 𝑓(0) = 𝑎(0 − ℎ)2 + 𝑘 = 𝑎ℎ2 + 𝑘
−𝑏
ℎ= , 𝑘 = 𝑓(ℎ)
2𝑎
Parabolic Graph of a Quadratic Function
y-intercept Axis of Symmetry
(𝟎, 𝒄) 𝑥=ℎ
Origin x- intercepts,
(𝟎, 𝟎) also called real
“zeros”
Distance k (Up/Down)
Distance h (Rt/Lft) This Parabola is
(from Origin) “Face Up”
(𝒂 > 𝟎)
Vertex: (𝒉, 𝒌)
“k” is the Min or Max value of the function.
“h” is the domain value that results in the Min/Max.
Practice Graphing Quadratic Functions 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 = 𝑎(𝑥 − ℎ)2 + 𝑘
Examples: Note: “a” is the same number
in both forms!
Graph the following Quadratic given in Graph the following Quadratic given in
General Form: 𝑓(𝑥) = −3𝑥 2 − 6𝑥 + 24 Standard (Vertex) Form: 𝑓(𝑥) = 3(𝑥 + 1)2 − 4
𝑎 𝑏 𝑐
Due to the “-“ sign in Vertex Form,” h” is the opposite of
Identify the Vertex: (Calculate) the number you see.
−𝑏 − (−6) 6
ℎ= = = = −1 Identify the Vertex: (from the formula)
2𝑎 2(−3) −6
(ℎ, 𝑘) = (−1, −4)
𝑘 = 𝑓(ℎ) = −3(−1)2 − 6(−1) + 24
= 27 Find the x-intercept(s): (Square root property)
𝑉𝑒𝑟𝑡𝑒𝑥 = (ℎ, 𝑘) = (−1, 27) 𝑓(𝑥) = 3(𝑥 + 1)2 − 4 = 0
3(𝑥 + 1)2 = 4
Find the x-intercept(s): (Factor or use the 4
(𝑥 + 1)2 =
Quadratic Formula) 3
4
√(𝑥 + 1)2 = ±√
2 3
𝑓(𝑥) = −3𝑥 − 6𝑥 + 24 = 0
𝑓(𝑥) = −3(𝑥 2 + 2𝑥 − 8) = 0 𝑥+1=±
2
√3
𝑓(𝑥) = −3(𝑥 + 4)(𝑥 − 2) =0
2√3
𝑥 = −1 ±
𝑥+4=0 𝑥−2=0 3
𝑥 = −4 𝑥=2 2√3 2√3
x-intercepts: (−1 + , 0) , (−1 − , 0)
3 3
x-intercepts: (−4, 0), (2, 0)
Find the y-intercept: 𝑓(0) = 3(1)2 − 4 = −1
Find the y-intercept: (0, 𝑐) = (0, 24) = (0, −1)
Find the axis of symm: 𝑥 = −1 Find the axis of symm: 𝑥 = −1
Extra Points: Use point plotting if needed. Extra Points: Use point plotting if needed.
𝑎 <0, 𝑎 >0,
So facing DOWN So facing UP
Vertex (Max) x-intercepts
y-intercept y-intercept
x-intercepts Vertex (Min)
Axis of Symmetry
Axis of Symmetry
Range: (−∞, 𝑘]
Domain: (−∞, ∞) Range: [𝑘, ∞)
Domain: (−∞, ∞)
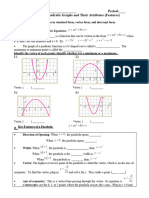
Practice Problems: Try these on your own!
Graph the following Quadratic Functions given in General Form. Find the Vertex, y-intercept,
and x-intercept(s) if they exist. State the Domain and the Range. Also find and show the Axis
of Symmetry. State whether the parabola opens up or down.
1. 𝑓(𝑥) = −𝑥 2 + 𝑥 + 6 2. 𝑓(𝑥 ) = 2𝑥 2 + 4𝑥 + 4
Answer: Answer:
1 25
Vertex: (2 , 4 ) Vertex: (−1, 2)
y-intercept: (0, 6) y-intercept: (0, 4)
x-intercept(s): (−2, 0), (3, 0) x-intercept(s): 𝑁𝑜𝑛𝑒
1
Axis of Symmetry: 𝑥 = Axis of Symmetry: 𝑥 = −1
2
Domain: ℝ or (−∞, ∞) Domain: ℝ or (−∞, ∞)
25
Range: (−∞, ] Range: [2, ∞)
4
Opens: Down Opens: Up
Graph the following Quadratic Functions given in Standard (Vertex) Form. Find the Vertex,
y-intercept, and x-intercept(s) if they exist. State the Domain and the Range. Also find and
show the Axis of Symmetry. State whether the parabola opens up or down.
1
3. 𝑓(𝑥) = 2(𝑥 − 2)2 − 3 4. 𝑓(𝑥) = − (𝑥 + 4)2 − 2
4
Answer: Answer:
Vertex: (2, −3) Vertex: (−4, −2)
y-intercept: (0, 5) y-intercept: (0, −6)
4+√6 4−√6
x-intercept(s): ( , 0) , ( , 0) x-intercept(s): 𝑁𝑜𝑛𝑒
2 2
Axis of Symmetry: 𝑥 = 2 Axis of Symmetry: 𝑥 = −4
Domain: ℝ or (−∞, ∞) Domain: ℝ or (−∞, ∞)
Range: [−3, ∞) Range: (−∞, −2]
Opens: Up Opens: Down