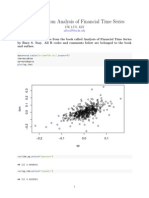
Practice of Introductory Time Series with R
YIK LUN, KEI
allen29@ucla.edu
Reference:
Cowpertwait, Paul SP, and Andrew V. Metcalfe. Introductory time series with
R. Springer Science & Business Media, 2009.
Onlinecourses.science.psu.edu,. 1.3 R Code For Two Examples In Lessons 1.1
And 1.2 | STAT 510. N.p., 2015. Web. 10 Aug. 2015.
This paper is a practice from the book called Introductory Time Series with R by by Paul Cowpertwait and Andrew Metcalfe, and from the website: onlinecourses.science.psu.edu/stat510/node/61.
All R codes and some comments below are belonged to the book and the website. Dataset
can be searched from Google.
Fact <- function(n) if (n == 1) 1 else n * Fact(n - 1) # one line function
Fact(6) # 6*5*4*3*2*1=720
## [1] 720
data(AirPassengers)
AP <- AirPassengers
aggregate(AP,FUN=mean) # to remove any seasonal effects
##
##
##
##
##
##
Time Series:
Start = 1949
End = 1960
Frequency = 1
[1] 126.6667 139.6667 170.1667 197.0000 225.0000 238.9167 284.0000
[8] 328.2500 368.4167 381.0000 428.3333 476.1667
plot(AP, ylab = "Passengers (1000's)")
500
300
100
Passengers (1000's)
1950
1952
1954
1956
1958
1960
Time
4000
2000
aggregate(AP)
plot(aggregate(AP)) # plot the sum for each year
1950
1952
1954
Time
1956
1958
1960
100
300
500
boxplot(AP ~ cycle(AP))
10
11
12
data <- "http://rci.rutgers.edu/~rwomack/UNRATE.csv"
data2<- "http://rci.rutgers.edu/~rwomack/CPIAUCSL.csv"
unemployment <- read.csv(data, row.name=1) # convert first column to row name
inflation <- read.csv(data2,row.name=1) # convert first column to row name
un.month.ts <- ts(unemployment$VALUE, start = c(1948,1), freq = 12)
un.annual.ts <- aggregate(un.month.ts)/12 # mean annual rate
in.month.ts <- ts(inflation$VALUE, start = c(1948, 1), freq = 12)
in.annual.ts <- aggregate(in.month.ts)/12 # mean annual rate
plot(un.month.ts, ylab = "unemployed (%)")
10
8
6
4
unemployed (%)
1950
1960
1970
1980
1990
2000
2010
Time
8
7
6
5
4
3
unemployed (%)
plot(un.annual.ts, ylab = "unemployed (%)")
1950
1960
1970
1980
Time
1990
2000
2010
10
5
0
inflation (%)
15
plot(in.month.ts, ylab = "inflation (%)")
1950
1960
1970
1980
1990
2000
2010
Time
10
5
0
inflation (%)
plot(in.annual.ts, ylab = "inflation (%)")
1950
1960
1970
1980
Time
1990
2000
2010
fivemonths<- window(un.month.ts, start = c(1996,2), end = c(1996,6), freq = 12)
fivemonths
##
Feb Mar Apr May Jun
## 1996 5.5 5.5 5.6 5.6 5.3
unemployment<-read.csv("/Users/air/Desktop/Econ 144/Chapter01Maine.csv")
un.month.ts<-ts(unemployment$unemploy,start=c(1996,1),freq=12)
un.Feb <- window(un.month.ts, start = c(1996,2), freq = TRUE) # capture only Feb
un.Aug <- window(un.month.ts, start = c(1996,8), freq = TRUE) # capture only Aug
Feb.ratio <- mean(un.Feb) / mean(un.month.ts)
# ratio = mean of Feb of all years / mean of all month of all years
Aug.ratio <- mean(un.Aug) / mean(un.month.ts)
Feb.ratio;Aug.ratio #On average, unemployment is 22% higher in February and 18% lower in August
## [1] 1.222529
## [1] 0.8163732
CBE <- read.csv("/Users/air/Desktop/Econ 144/Chapter01cbe.csv")
Elec.ts <- ts(CBE[, 3], start = 1958, freq = 12)
Beer.ts <- ts(CBE[, 2], start = 1958, freq = 12)
Choc.ts <- ts(CBE[, 1], start = 1958, freq = 12)
plot(cbind(Elec.ts, Beer.ts, Choc.ts))
8000
2002000
100
6000
2000
Choc.ts
Beer.ts
Elec.ts
cbind(Elec.ts, Beer.ts, Choc.ts)
1960
1965
1970
1975
Time
1980
1985
1990
600
500
400
300
Air passengers / 1000's
AP.elec <- ts.intersect(AP, Elec.ts) # only time frame that overlaps
AP <- AP.elec[,1]; Elec <- AP.elec[,2]
plot(AP, ylab = "Air passengers / 1000's")
1958.0
1958.5
1959.0
1959.5
Time
plot(Elec, ylab = "Electricity production / MkWh")
1960.0
1960.5
1961.0
2000
1600
Electricity production / MkWh
1958.0
1958.5
1959.0
1959.5
1960.0
1960.5
Time
2000
1600
Electricity production / MWh
plot(as.vector(AP), as.vector(Elec),xlab = "Air passengers / 1000's",
ylab = "Electricity production / MWh")
abline(reg = lm(Elec ~ AP),col="red") # not causation
300
350
400
450
500
Air passengers / 1000's
550
600
1961.0
0.0
0.5
1.0
Global.ts
0.5
Global<-scan("http://elena.aut.ac.nz/~pcowpert/ts/global.dat")
Global.ts <- ts(Global, st = c(1856, 1), end = c(2005, 12), freq = 12)
Global.annual <- aggregate(Global.ts, FUN = mean)
plot(Global.ts)
1900
1950
Time
plot(Global.annual)
2000
0.4
0.0
0.4
Global.annual
1900
1950
2000
Time
0.4
0.0
0.4
New.series
0.8
New.series <- window(Global.ts, start=c(1970, 1), end=c(2005, 12))
plot(New.series)
abline(reg=lm(New.series ~ time(New.series)),col="red") # function ot time t
1970
1975
1980
1985
1990
Time
10
1995
2000
2005
plot(decompose(Elec.ts))
12000
100002000
500 2000
600500
600 0
random seasonal trend observed
Decomposition of additive time series
1960
1965
1970
1975
Time
Elec.decom <- decompose(Elec.ts, type = "mult")
plot(Elec.decom)
11
1980
1985
1990
12000
100002000
1.05 2000
1.02 0.90
0.94
random seasonal trend observed
Decomposition of multiplicative time series
1960
1965
1970
1975
1980
1985
1990
Time
2000
6000
10000 14000
Trend <- Elec.decom$trend
Seasonal <- Elec.decom$seasonal
ts.plot(cbind(Trend, Trend * Seasonal), lty = 1:2) # trend and seasonal effects
1960
1965
1970
1975
Time
12
1980
1985
1990
Herald.dat <- read.table("http://elena.aut.ac.nz/~pcowpert/ts/Herald.dat",header=TRUE)
attach (Herald.dat)
x <- CO; y <- Benzoa; n <- length(x)
plot(x,y)
abline(h=mean(y),col="red")
abline(v=mean(x),col="blue")
10
15
x
sum((x - mean(x))*(y - mean(y))) / (n - 1) # covariance
## [1] 5.511042
mean((x - mean(x)) * (y - mean(y))) # covariance
## [1] 5.166602
cov(x, y) # covariance
## [1] 5.511042
cov(x,y) / (sd(x)*sd(y)) # correlation
## [1] 0.3550973
13
20
cor(x,y) # correlation
## [1] 0.3550973
0
500
ts(waveht)
500
wave.dat <- read.table ("http://elena.aut.ac.nz/~pcowpert/ts/wave.dat", header=T)
attach(wave.dat)
plot(ts(waveht))
100
200
Time
plot(ts(waveht[1:60]))
14
300
400
600
200
200
600
ts(waveht[1:60])
10
20
30
40
50
60
Time
acf(waveht)$acf[2]
0.5
0.0
ACF
0.5
1.0
Series waveht
10
15
Lag
## [1] 0.4702564
15
20
25
500
0
500
waveht[2:397]
plot(waveht[1:396],waveht[2:397])
500
500
waveht[1:396]
acf(waveht, type = c("covariance"))$acf[2]
20000
20000
ACF (cov)
60000
Series waveht
10
15
Lag
16
20
25
## [1] 33328.39
data(AirPassengers)
AP <- AirPassengers
acf(AP)
0.2
0.2
ACF
0.6
1.0
Series AP
0.0
0.5
1.0
Lag
AP.decom <- decompose(AP, "multiplicative")
plot(ts(AP.decom$random[7:138]))
17
1.5
1.10
1.05
1.00
0.95
0.90
ts(AP.decom$random[7:138])
20
40
60
80
100
120
Time
acf(AP.decom$random[7:138])
0.2
0.2
ACF
0.6
1.0
Series AP.decom$random[7:138]
10
15
20
Lag
#The figure suggests either a cosine shape that is whether a characteristic of an autoregressive model of
order 2 or a not effective seasonal adjustment.
18
The reduction in the standard deviation indicates that the seasonal
adjustment has been very effective.
sd(AP[7:138]) # standard deviation of the original series
## [1] 109.4187
sd(AP[7:138] - AP.decom$trend[7:138]) #original series subtracting the trend
## [1] 41.11491
sd(AP.decom$random[7:138]) # standard deviation after seasonal adjustment
## [1] 0.0333884
70
90
mort
110
130
mort=scan("http://anson.ucdavis.edu/~shumway/cmort.dat")
plot(mort, type="o") # plot of mortality rate
100
200
300
Index
mort=ts(mort)
mortdiff=diff(mort,1) # creates a variable = x(t) x(t-1)
plot(mortdiff,type="o") # plot of first differences
19
400
500
20
10
0
20 10
mortdiff
100
200
300
400
Time
acf(mortdiff,xlim=c(1,24)) # plot of first differences, for 24 lags
0.5
0.0
ACF
0.5
1.0
Series mortdiff
10
15
Lag
20
20
500
10
0
20 10
mortdifflag1
20
mortdifflag1=lag(mortdiff,-1)
plot(mortdifflag1,type="o")
100
200
300
400
500
Time
y=cbind(mortdiff,mortdifflag1) # bind first differences and lagged first differences
mortdiffar1=lm(y[,1]~y[,2]) # AR(1) regression for first differences
summary(mortdiffar1) # regression results
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
##
Call:
lm(formula = y[, 1] ~ y[, 2])
Residuals:
Min
1Q
-19.2758 -3.8753
Median
-0.0953
3Q
3.5725
Max
20.8169
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.04627
0.25900 -0.179
0.858
y[, 2]
-0.50636
0.03838 -13.195
<2e-16 ***
--Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.826 on 504 degrees of freedom
(2 observations deleted due to missingness)
Multiple R-squared: 0.2568, Adjusted R-squared: 0.2553
F-statistic: 174.1 on 1 and 504 DF, p-value: < 2.2e-16
21
acf(mortdiffar1$residuals, xlim = c(1,24)) # ACF of residuals for 24 lags.
0.4
0.0
ACF
0.8
Series mortdiffar1$residuals
10
15
Lag
22
20