基于Python与MQL5的特征工程(第三部分):价格角度(2)——极坐标(Polar Coordinates)法
将价格变化转化为角度变化的探索热情未减。正如本系列前文所述,要成功将价格水平变化转化为能代表该变化的角度值,仍需克服诸多挑战。
在社区论坛和帖子中,最常被提及的局限性之一是:此类计算背后缺乏可解释的实际意义。经验丰富的社区成员往往会指出:角度存在于两条直线之间,因此试图通过价格变化计算角度在现实世界中并无实际意义。
对于希望计算价格变化所形成角度的交易者而言,缺乏现实世界中的可解释性仅是众多待克服的挑战之一。在前文中,我们曾尝试通过替换X轴的时间变量,使生成的角度成为价格水平的比率,从而赋予其一定的解释意义。然而在探索过程中,我们发现经此转换后的数据集极易出现大量“无穷大”值。欲快速回顾前文观察结果的读者,可点击此处查阅相关文章。
在尝试将价格变化转化为对应角度变化时,由于缺乏明确的现实世界意义,相关领域的系统性资料极为有限。
我们将从全新的角度解决价格到角度的转换问题。本次,我们将采用比首次尝试时更数学严谨且稳健的方法攻克这一难题。熟悉极坐标的读者可直接跳转至“MQL5实战入门”章节,查看这些数学工具在MQL5中的实现方式。
否则,我们将从基础概念入手,理解极坐标的本质,并建立直观认知:将其应用于MetaTrader 5终端中,计算由价格变化形成的角度,并将这些信号转化为交易策略。也就是说:
- 我们的解决方案具有现实意义。
- 我们也同时解决此前无限值或未定义值的问题。
极坐标的定义与应用价值
当我们使用GPS技术或简单的电子表格时,实际上依赖的是笛卡尔坐标系(Cartesian Coordinates)。这是一种通过两组垂直轴表示平面内点的数学系统。
在笛卡尔坐标系中,任意一点由(x, y)坐标对表示:x代表该点与原点的水平距离,y代表该点与原点的垂直距离。
如果需研究具有周期性成分或圆周运动的过程,极坐标比笛卡尔坐标系更适用。极坐标通过两个参数表示平面内点:与参考点(原点)的径向距离和与参考方向的夹角(逆时针方向为正)
金融市场常表现出近乎周期性的重复模式。因此极坐标可能成为其理想表示方式。通过将价格水平表示为极坐标对(r, θ),可以自然得出交易者所需计算的价格变化角度。
极坐标以(r, θ)对表示,其中:
- r:表示径向距离(与原点的距离)
- θ:表示参考方向测量的角度
借助MQL5矩阵与向量API的三角函数,可无缝将价格变化转换为表示价格变动的角度。
为实现目标,我们需要先熟悉在讨论中会使用的术语。首先,我们必须定义将被转换的x和y输入。在讨论中,我们将x设置为交易品种的开盘价,y设置为收盘价。

图例1:定义待转换为极坐标的笛卡尔坐标点
在定义好x轴(开盘价)与y轴(收盘价)的输入值后,下一步我们需要计算极坐标对(r, θ)中的首个元素——径向距离r(即该点与原点的距离)。
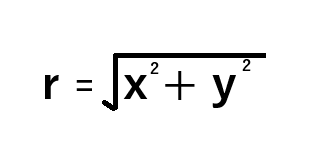
图例2:基于笛卡尔坐标(x, y)计算径向距离r的闭合公式
从几何角度理解,极坐标可视为对圆的描述。径向距离r与x轴形成的夹角即为θ。因此,极坐标通过r与θ的组合,能够等效传递与笛卡尔坐标(x, y)相同的信息。如图例3所示,当x与y在坐标系中呈现为直角三角形的两条直角边时,可通过x边与y边应用勾股定理计算径向距离r。
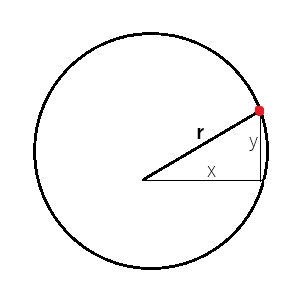
图例3:极坐标可视为对圆上点的描述
径向距离r与x轴的夹角θ,赋予了极坐标实际的分析价值。在此简单示例中,θ反映了开盘价与收盘价变动所形成趋势的方向。如下图所示,θ可通过计算收盘价与开盘价的反正切值得出:
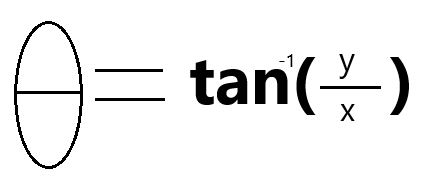
图例4:基于开盘价(x)与收盘价(y)计算角度θ
给定任意极坐标(r, θ),可通过以下两个公式轻松还原其原始价格水平:
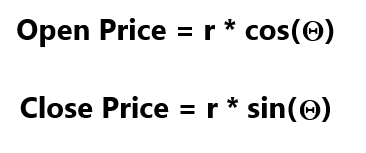
图例5:极坐标转换为笛卡尔坐标的方法
截至目前,我们讨论了4个公式,但仅后3个公式涉及角度θ。第一个计算r的公式与θ无关。后3个公式均包含θ,并且可以明确区分。这些三角函数的导数均为大众熟知的结果,可在任意基础微积分教材或在线资源中查询。
我们将利用这3个导数作为附加的输入,训练计算机学习角度变化与价格水平变化的关联性。
MQL5入门指南
让我们开始吧。我们首先需要编写一个MQL5脚本,从MetaTrader 5终端获取历史市场数据,并计算生成的角度值。
我们需要定义所创建CSV文件名,并指定要获取的K线数量。由于不同经纪商可供获取的历史K线数量可能不同,因此该参数已设为脚本的外部输入项。
#property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs //---File name string file_name = _Symbol + " " + " Polar Coordinates.csv"; //---Amount of data requested input int size = 100; int size_fetch = size + 100;
当执行脚本时,我们将创建一个文件句柄,用于把价格水平及其对应的角度变化写入文件。
void OnStart() { //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i=size;i>0;i--){ if(i == size){ FileWrite(file_handle,"Time","Open","High","Low","Close","R","Theta","X Derivatie","Y Derivative","Theta Derivative"); } else{
接下来,我们使用图例2中讨论的公式计算r。
double r = MathSqrt(MathPow(iOpen(_Symbol,PERIOD_CURRENT,i),2) + MathPow(iClose(_Symbol,PERIOD_CURRENT,i),2));
θ通过y与x比值的反正切计算得出。MQL5 API已为我们提供了相应函数。
double theta = MathArctan2(iClose(_Symbol,PERIOD_CURRENT,i),iOpen(_Symbol,PERIOD_CURRENT,i));
回顾上面图例5所给出的计算x(开盘价)的公式。我们可对该式关于θ求导,得到开盘价的一阶导数。如您所知,cos( )的导数为-sin( )。
double derivative_x = r * (-(MathSin(theta)));
同样地,由于我们已经掌握三角函数的导数,因此也可以求出y的导数。
double derivative_y = r * MathCos(theta);
最后,我们已知角度θ的一阶导数。然而,MQL5 API并未直接提供三角函数运算,因此需通过数学恒等式将其替换为MQL5内置函数可处理的形式。
double derivative_theta = (1/MathPow(MathCos(theta),2));
既然已计算出角度值,我们即可着手将数据写入输出文件。
FileWrite(file_handle,iTime(_Symbol,PERIOD_CURRENT,i), iOpen(_Symbol,PERIOD_CURRENT,i), iHigh(_Symbol,PERIOD_CURRENT,i), iLow(_Symbol,PERIOD_CURRENT,i), iClose(_Symbol,PERIOD_CURRENT,i), r, theta, derivative_x, derivative_y, derivative_y ); } } FileClose(file_handle); } //+---------
数据分析
既然数据已经以CSV格式导出,我们即可利用其训练计算机识别交易形成的角度。为加速开发进程,我们将调用多个Python库实现功能。
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt
对数据进行标注,记录次日价格水平是上涨还是下跌。
data = pd.read_csv("EURUSD Polar Coordinates.csv") data["UP DOWN"] = 0 data.loc[data["Close"] < data["Close"].shift(-1),"UP DOWN"] = 1 data
以下是我们寻找的交易信号。请注意,当原始数据集中的r与θ同时增大时,价格水平从未下跌。调用该pandas未返回任何结果,这恰好印证了极坐标对在现实交易中的实际意义。掌握r与θ的未来值,等同于预知未来价格水平。
data.loc[(data["R"] < data["R"].shift(-1)) & (data['Theta'] < data['Theta'].shift(-1)) & (data['Close'] > data['Close'].shift(-1))
同理,若我们执行相同的查询但方向相反——即寻找r与θ均增大,但未来价格下跌的实例——则会发现pandas仍返回0条匹配结果。
data.loc[(data["R"] > data["R"].shift(-1)) & (data['Theta'] > data['Theta'].shift(-1)) & (data['Close'] < data['Close'].shift(-1))]
因此,当计算机预测r与θ的未来值将大于当前值时,即可生成交易信号。接下来,我们可将价格数据以极坐标圆上的点进行可视化。如图例6所示,数据仍难以实现有效地分离。
data['Theta_rescaled'] = (data['Theta'] - data['Theta'].min()) / (data['Theta'].max() - data['Theta'].min()) * (2 * np.pi) data['R_rescaled'] = (data['R'] - data['R'].min()) / (data['R'].max() - data['R'].min()) # Create the polar plot fig, ax = plt.subplots(subplot_kw={'projection': 'polar'}) # Plot data points on the polar axis ax.scatter(data['Theta_rescaled'], data['R_rescaled'],c=data["UP DOWN"], cmap='viridis', edgecolor='black', s=100) # Add plot labels ax.set_title("Polar Plot of OHLC Points") plt.colorbar(plt.cm.ScalarMappable(cmap='viridis'), ax=ax, label='1(UP) | O(DOWN)') plt.show()
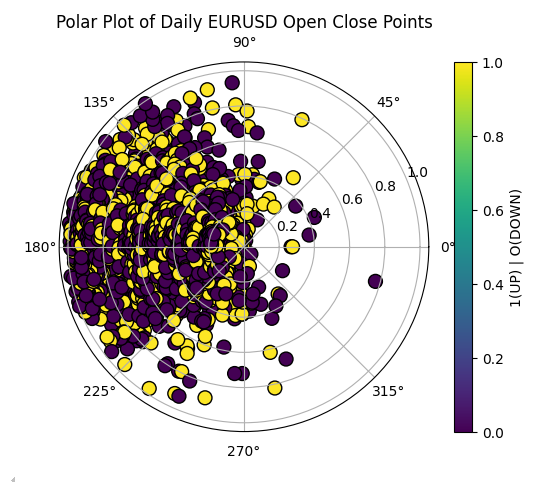
图例6:以极坐标圆上的极点形式可视化价格数据
让我们快速核查数据中是否存在空值。
data.isna().any()
图例7:检查所有值是否为空
数据建模
完美定义所有数据值。接下来,我们需要对数据进行标注。再次提醒,我们的预测目标是θ与r的未来值。
LOOK_AHEAD = 1 data['R Target'] = data['R'].shift(-LOOK_AHEAD) data['Theta Target'] = data['Theta'].shift(-LOOK_AHEAD) data.dropna(inplace=True) data.reset_index(drop=True,inplace=True)
请记住,我们需剔除最后两年的数据,以便将其作为模型应用的测试集。
#Let's entirely drop off the last 2 years of data _ = data.iloc[-((365 * 2) + 230):,:] data = data.iloc[:-((365 * 2) + 230),:] data
图例8:剔除最后两年数据后的数据集
当前,使用现有数据训练计算机模型。我们选择梯度提升树作为模型,因其特别擅长捕捉变量间的交互效应。
from sklearn.ensemble import GradientBoostingRegressor from sklearn.model_selection import train_test_split,TimeSeriesSplit,cross_val_score
现定义时间序列分割对象。
tscv = TimeSeriesSplit(n_splits=5,gap=LOOK_AHEAD) 定义输入和目标。
X = data.columns[1:-5] y = data.columns[-2:]
将数据分为训练和测试两部分。
train , test = train_test_split(data,test_size=0.5,shuffle=False)
现在划分训练集与测试集。
train_X = train.loc[:,X] train_y = train.loc[:,y] test_X = test.loc[:,X] test_y = test.loc[:,y]
需要标准化训练和测试的划分。
mean_scores = train_X.mean() std_scores = train_X.std()
缩放数据。
train_X = ((train_X - mean_scores) / std_scores) test_X = ((test_X - mean_scores) / std_scores)
初始化模型。
model = GradientBoostingRegressor()
准备一张表格用于存储结果。
results = pd.DataFrame(index=["Train","Test"],columns=["GBR"])
调整模型以预测r。
results.iloc[0,0] = np.mean(np.abs(cross_val_score(model,train_X,train_y["R Target"],cv=tscv))) results.iloc[1,0] = np.mean(np.abs(cross_val_score(model,test_X,test_y["R Target"],cv=tscv))) results
| GBR | |
|---|---|
| 训练 | 0.76686 |
| 测试 | 0.89129 |
调整模型以预测θ。
results.iloc[0,0] = np.mean(np.abs(cross_val_score(model,train_X,train_y["Theta Target"],cv=tscv))) results.iloc[1,0] = np.mean(np.abs(cross_val_score(model,test_X,test_y["Theta Target"],cv=tscv))) results
| GBR | |
|---|---|
| 训练 | 0.368166 |
| 测试 | 0.110126 |
导出到ONNX
加载我们需要的库。
import onnx import skl2onnx from skl2onnx.common.data_types import FloatTensorType
初始化两个模型。
r_model = GradientBoostingRegressor() theta_model = GradientBoostingRegressor()
将全局标准化分数存储为CSV格式文件。
mean_scores = data.loc[:,X].mean() std_scores = data.loc[:,X].std() mean_scores.to_csv("EURUSD Polar Coordinates Mean.csv") std_scores.to_csv("EURUSD Polar Coordinates Std.csv")
初始化整个数据集。
data[X] = ((data.loc[:,X] - mean_scores) / std_scores)
根据缩放的数据调整模型。
r_model.fit(data.loc[:,X],data.loc[:,'R Target']) theta_model.fit(data.loc[:,X],data.loc[:,'Theta Target'])
定义输入形状。
initial_types = [("float_input",FloatTensorType([1,len(X)]))]
准备用于保存的ONNX原型。
r_model_proto = skl2onnx.convert_sklearn(r_model,initial_types=initial_types,target_opset=12) theta_model_proto = skl2onnx.convert_sklearn(theta_model,initial_types=initial_types,target_opset=12)
保存ONNX文件。
onnx.save(r_model_proto,"EURUSD D1 R Model.onnx") onnx.save(theta_model_proto,"EURUSD D1 Theta Model.onnx")
MQL5入门指南
现在,我们准备构建我们的交易应用程序。
//+------------------------------------------------------------------+ //| EURUSD Polar EA.mq5 | //| Gamuchirai Ndawana | //| https://www.mql5.com/en/users/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| System Constants | //+------------------------------------------------------------------+ #define ONNX_INPUTS 9 //The total number of inputs for our onnx model #define ONNX_OUTPUTS 1 //The total number of outputs for our onnx model #define TF_1 PERIOD_D1 //The system's primary time frame #define TRADING_VOLUME 0.1 //The system's trading volume
作为系统资源加载ONNX模型。
//+------------------------------------------------------------------+ //| System Resources | //+------------------------------------------------------------------+ #resource "\\Files\\EURUSD D1 R Model.onnx" as uchar r_model_buffer[]; #resource "\\Files\\EURUSD D1 Theta Model.onnx" as uchar theta_model_buffer[];
定义我们的全局变量。我们将使用其中一些变量标准化我们的数据,存储ONNX模型的预测等等。
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ double mean_values[] = {1.1884188643844635,1.1920754015799868,1.1847545720868993,1.1883860236998025,1.6806588395310122,0.7853854898794739,-1.1883860236998025,1.1884188643844635,1.1884188643844635}; double std_values[] = {0.09123896995032886,0.09116171300874902,0.0912656190371797,0.09120265318308786,0.1289537623737421,0.0021932437785043796,0.09120265318308786,0.09123896995032886,0.09123896995032886}; double current_r,current_theta; long r_model,theta_model; vectorf r_model_output = vectorf::Zeros(ONNX_OUTPUTS); vectorf theta_model_output = vectorf::Zeros(ONNX_OUTPUTS); double bid,ask; int ma_o_handler,ma_c_handler,state; double ma_o_buffer[],ma_c_buffer[];
加载交易库。
//+------------------------------------------------------------------+ //| Library | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
我们的交易应用主要由事件处理器构成。在应用生命周期的每个阶段,我们将调用专用函数执行与当前目标对应的任务。因此,初始化阶段会设置技术指标,而当新价格数据到达时,则更新这些指标的读数。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- if(!setup()) { Comment("Failed To Load Corretly"); return(INIT_FAILED); } Comment("Started"); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- OnnxRelease(r_model); OnnxRelease(theta_model); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- update(); } //+------------------------------------------------------------------+
从ONNX模型获取预测结果。请注意,我们将所有模型输入强制转换为浮点类型,以确保模型接收到符合其预期格式和大小的数据。
//+------------------------------------------------------------------+ //| Get a prediction from our models | //+------------------------------------------------------------------+ void get_model_prediction(void) { //Define theta and r double o = iOpen(_Symbol,PERIOD_CURRENT,1); double h = iHigh(_Symbol,PERIOD_CURRENT,1); double l = iLow(_Symbol,PERIOD_CURRENT,1); double c = iClose(_Symbol,PERIOD_CURRENT,1); current_r = MathSqrt(MathPow(o,2) + MathPow(c,2)); current_theta = MathArctan2(c,o); vectorf model_inputs = { (float) o, (float) h, (float) l, (float) c, (float) current_r, (float) current_theta, (float)(current_r * (-(MathSin(current_theta)))), (float)(current_r * MathCos(current_theta)), (float)(1/MathPow(MathCos(current_theta),2)) }; //Standardize the model inputs for(int i = 0; i < ONNX_INPUTS;i++) { model_inputs[i] = (float)((model_inputs[i] - mean_values[i]) / std_values[i]); } //Get a prediction from our model OnnxRun(r_model,ONNX_DATA_TYPE_FLOAT,model_inputs,r_model_output); OnnxRun(theta_model,ONNX_DATA_TYPE_FLOAT,model_inputs,theta_model_output); //Give our prediction Comment(StringFormat("R: %f \nTheta: %f\nR Forecast: %f\nTheta Forecast: %f",current_r,current_theta,r_model_output[0],theta_model_output[0])); }
每当有新的价格出现时,请更新系统。
//+------------------------------------------------------------------+ //| Update system state | //+------------------------------------------------------------------+ void update(void) { static datetime time_stamp; datetime current_time = iTime(_Symbol,TF_1,0); bid = SymbolInfoDouble(_Symbol,SYMBOL_BID); ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK); if(current_time != time_stamp) { CopyBuffer(ma_o_handler,0,0,1,ma_o_buffer); CopyBuffer(ma_c_handler,0,0,1,ma_c_buffer); time_stamp = current_time; get_model_prediction(); manage_account(); if(PositionsTotal() == 0) get_signal(); } }
管理交易账户。如果某笔交易出现亏损,我们将立即平仓止损。否则,如果已进场但均线交叉形态动摇我们对持仓的信心,则立即平仓离场。
//+------------------------------------------------------------------+ //| Manage the open positions we have in the market | //+------------------------------------------------------------------+ void manage_account() { if(AccountInfoDouble(ACCOUNT_BALANCE) < AccountInfoDouble(ACCOUNT_EQUITY)) { while(PositionsTotal() > 0) Trade.PositionClose(Symbol()); } if(state == 1) { if(ma_c_buffer[0] < ma_o_buffer[0]) Trade.PositionClose(Symbol()); } if(state == -1) { if(ma_c_buffer[0] > ma_o_buffer[0]) Trade.PositionClose(Symbol()); } }
设置系统变量,如技术指标和ONNX模型。
//+------------------------------------------------------------------+ //| Setup system variables | //+------------------------------------------------------------------+ bool setup(void) { ma_o_handler = iMA(Symbol(),TF_1,50,0,MODE_SMA,PRICE_CLOSE); ma_c_handler = iMA(Symbol(),TF_1,10,0,MODE_SMA,PRICE_CLOSE); r_model = OnnxCreateFromBuffer(r_model_buffer,ONNX_DEFAULT); theta_model = OnnxCreateFromBuffer(theta_model_buffer,ONNX_DEFAULT); if(r_model == INVALID_HANDLE) return(false); if(theta_model == INVALID_HANDLE) return(false); ulong input_shape[] = {1,ONNX_INPUTS}; ulong output_shape[] = {1,ONNX_OUTPUTS}; if(!OnnxSetInputShape(r_model,0,input_shape)) return(false); if(!OnnxSetInputShape(theta_model,0,input_shape)) return(false); if(!OnnxSetOutputShape(r_model,0,output_shape)) return(false); if(!OnnxSetOutputShape(theta_model,0,output_shape)) return(false); return(true); }
检查是否存在交易信号。我们主要核查均线交叉策略的指向性。随后,将验证ONNX模型给出的预期结果。因此,若均线交叉显示看跌信号,但r与θ两个ONNX模型给出看涨信号,则暂不进场,直至两套系统达成一致。
//+------------------------------------------------------------------+ //| Check if we have a trading signal | //+------------------------------------------------------------------+ void get_signal(void) { if(ma_c_buffer[0] > ma_o_buffer[0]) { if((r_model_output[0] < current_r) && (theta_model_output[0] < current_theta)) { return; } if((r_model_output[0] > current_r) && (theta_model_output[0] > current_theta)) { Trade.Buy(TRADING_VOLUME * 2,Symbol(),ask,0,0); Trade.Buy(TRADING_VOLUME * 2,Symbol(),ask,0,0); state = 1; return; } Trade.Buy(TRADING_VOLUME,Symbol(),ask,0,0); state = 1; return; } if(ma_c_buffer[0] < ma_o_buffer[0]) { if((r_model_output[0] > current_r) && (theta_model_output[0] > current_theta)) { return; } if((r_model_output[0] < current_r) && (theta_model_output[0] < current_theta)) { Trade.Sell(TRADING_VOLUME * 2,Symbol(),bid,0,0); Trade.Sell(TRADING_VOLUME * 2,Symbol(),bid,0,0); state = -1; return; } Trade.Sell(TRADING_VOLUME,Symbol(),bid,0,0); state = -1; return; } }
我们没有使用未定义的系统常数。
//+------------------------------------------------------------------+ //| Undefine system variables we don't need | //+------------------------------------------------------------------+ #undef ONNX_INPUTS #undef ONNX_OUTPUTS #undef TF_1 //+------------------------------------------------------------------+
系统测试
现在,让我们开始测试系统。再次提醒,在数据预处理阶段,我们删除了2022年1月1日的数据,以确保回测结果能真实反映策略在完全未见过的数据上的表现。
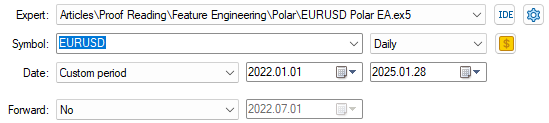
图例9:回测设置
现在指定初始帐户设置。
图例10:针对样本外数据的第二轮关键回测参数配置
我们可以观察到新系统生成的交易信号净值曲线。策略初始资金为5000美元,最终资金约7000美元,收益良好,激励我们持续优化策略。
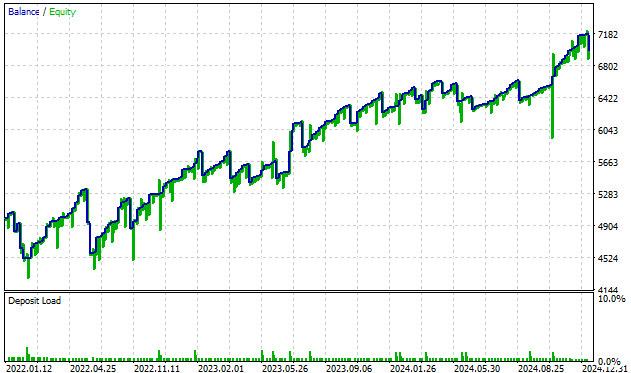
图例11:基于角度变换信号的回测结果
让我们对结果进行详细分析。该策略在样本外数据上的准确率达到88%。这一数据颇具鼓舞性,可为读者提供良好的起点——通过扩展我们在本应用中演示的MetaTrader 5终端功能,构建自有应用。或者可以将我们的框架作为参考,完全替换为读者自研的交易策略。
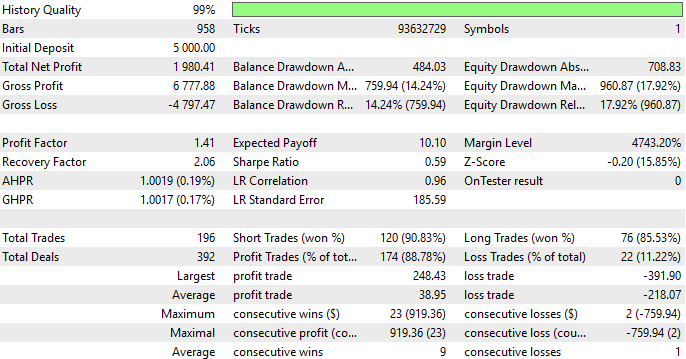
图例12:回测结果深度解析
结论
今日展示的解决方案,演示了如何通过将价格水平变化转化为角度变化,挖掘潜在交易优势。我们的方法为您提供了一个简洁优雅的框架,既融合交易逻辑又兼顾数学逻辑,实现二者的最优平衡。更重要的是,不同于盲目预测价格的普通市场参与者,您现在掌握了替代性预测目标——这些目标与价格本身同等重要,且比价格本身更易实现稳定地预测。
| 附件文件 | 描述 |
|---|---|
| 极坐标获取数据 | 为获取价格数据并将其转换为极坐标而定制的脚本。 |
| 欧元兑美元极坐标EA | 基于角度变化生成信号交易的EA |
| 欧元兑美元日线级(D1)r模型 | 负责预测r未来值的ONNX模型 |
| 欧元兑美元日线级(D1)θ模型 | 负责预测θ未来值的ONNX模型 |
| 欧元兑美元极坐标 | 用于分析MQL5脚本获取数据的Jupyter笔记本电脑 |