Permutations of given String

Last Updated : 23 Jul, 2025

Given a string s, the task is to return all permutations of a given string in lexicographically sorted order.

Note: A permutation is the rearrangement of all the elements of a string. Duplicate arrangement can exist.

Examples:

Input: s = "ABC"
Output: "ABC", "ACB", "BAC", "BCA", "CAB", "CBA"
Input: s = "XY"
Output: "XY", "YX"
Input: s = "AAA"
Output: "AAA", "AAA", "AAA", "AAA", "AAA", "AAA"

The idea is to use backtracking to generate all possible permutations of given string s. To do so, first initialize an array of string ans[] to store all the permutations. Start from the 0^th index and for each index i, swap the value s[i] with all the elements in its right i.e. from i+1 to n-1, and recur to the index i + 1. If the index i is equal to n, store the resultant string in ans[], else keep operating similarly for all other indices. Thereafter, swap back the values to original values to initiate backtracking. At last sort the array ans[].

illustration:

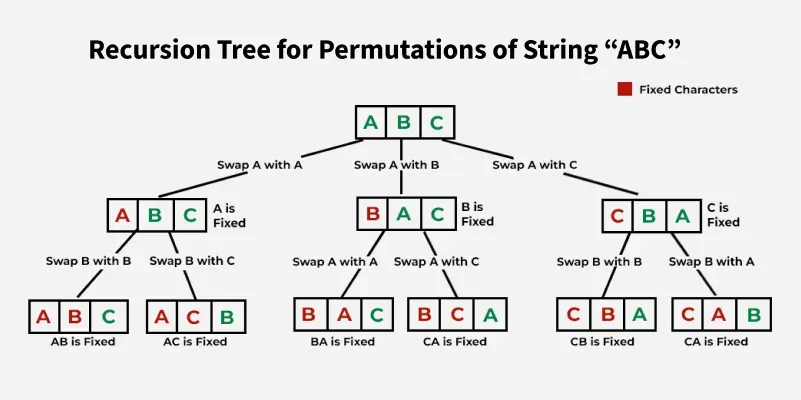
Below is the implementation of the above approach:

C++

// C++ Program to generate all unique // permutations of a string #include <bits/stdc++.h> using namespace std; // Recursive function to generate  // all permutations of string s void recurPermute(int index, string &s,  vector<string> &ans) {  // Base Case  if (index == s.size()) {  ans.push_back(s);  return;  }  // Swap the current index with all  // possible indices and recur  for (int i = index; i < s.size(); i++) {  swap(s[index], s[i]);  recurPermute(index + 1, s, ans);  swap(s[index], s[i]);  } } // Function to find all unique permutations vector<string> findPermutation(string &s) {  // Stores the final answer  vector<string> ans;  recurPermute(0, s, ans);  // sort the resultant vector  sort(ans.begin(), ans.end());  return ans; } int main() {  string s = "ABC";  vector<string> res = findPermutation(s);  for(auto x: res) {  cout << x << " ";  }  return 0; }

Java

// Java Program to generate all unique // permutations of a string import java.util.*; class GfG {  // Recursive function to generate   // all permutations of string s  static void recurPermute(int index, StringBuilder s,   List<String> ans) {  // Base Case  if (index == s.length()) {  ans.add(s.toString());  return;  }  // Swap the current index with all  // possible indices and recur  for (int i = index; i < s.length(); i++) {  swap(s, index, i);  recurPermute(index + 1, s, ans);  swap(s, index, i);  }  }  // Swap characters at positions i and j  static void swap(StringBuilder s, int i, int j) {  char temp = s.charAt(i);  s.setCharAt(i, s.charAt(j));  s.setCharAt(j, temp);  }  // Function to find all unique permutations  static List<String> findPermutation(String s) {  // Stores the final answer  List<String> ans = new ArrayList<>();  StringBuilder str = new StringBuilder(s);  recurPermute(0, str, ans);  // sort the resultant list  Collections.sort(ans);  return ans;  }  public static void main(String[] args) {  String s = "ABC";  List<String> res = findPermutation(s);  for (String x : res) {  System.out.print(x + " ");  }  } }

Python

# Python Program to generate all unique # permutations of a string # Recursive function to generate  # all permutations of string s def recurPermute(index, s, ans): # Base Case if index == len(s): ans.append("".join(s)) return # Swap the current index with all # possible indices and recur for i in range(index, len(s)): s[index], s[i] = s[i], s[index] recurPermute(index + 1, s, ans) s[index], s[i] = s[i], s[index] # Function to find all unique permutations def findPermutation(s): # Stores the final answer ans = [] recurPermute(0, list(s), ans) # sort the resultant list ans.sort() return ans if __name__ == "__main__": s = "ABC" res = findPermutation(s) for x in res: print(x, end=" ")

// C# Program to generate all unique // permutations of a string using System; using System.Collections.Generic; class GfG {  // Recursive function to generate   // all permutations of string s  static void recurPermute(int index, char[] s,   List<string> ans) {  // Base Case  if (index == s.Length) {  ans.Add(new string(s));  return;  }  // Swap the current index with all  // possible indices and recur  for (int i = index; i < s.Length; i++) {  Swap(s, index, i);  recurPermute(index + 1, s, ans);  Swap(s, index, i);  }  }  // Swap characters at positions i and j  static void Swap(char[] s, int i, int j) {  char temp = s[i];  s[i] = s[j];  s[j] = temp;  }  // Function to find all unique permutations  static List<string> findPermutation(string s) {  // Stores the final answer  List<string> ans = new List<string>();  recurPermute(0, s.ToCharArray(), ans);  // sort the resultant list  ans.Sort();  return ans;  }  static void Main(string[] args) {  string s = "ABC";  List<string> res = findPermutation(s);  foreach (string x in res) {  Console.Write(x + " ");  }  } }

JavaScript

// JavaScript Program to generate all unique // permutations of a string // Recursive function to generate  // all permutations of string s function recurPermute(index, s, ans) {  // Base Case  if (index === s.length) {  ans.add(s.join(""));  return;  }  // Swap the current index with all  // possible indices and recur  for (let i = index; i < s.length; i++) {  [s[index], s[i]] = [s[i], s[index]];  recurPermute(index + 1, s, ans);  [s[index], s[i]] = [s[i], s[index]];  } } // Function to find all unique permutations function findPermutation(s) {  // sort input string  s = s.split("").sort();  // Stores all unique permutations  let res = new Set();  recurPermute(0, s, res);  // Convert Set to Array for the final answer  return Array.from(res).sort(); } const s = "ABC"; const res = findPermutation(s); console.log(res.join(" "));