Range sum query using Sparse Table
Last Updated : 21 Aug, 2022
We have an array arr[]. We need to find the sum of all the elements in the range L and R where 0 <= L <= R <= n-1. Consider a situation when there are many range queries.
Examples:
Input : 3 7 2 5 8 9 query(0, 5) query(3, 5) query(2, 4) Output : 34 22 15
Note : array is 0 based indexed and queries too.
Since there are no updates/modifications, we use the Sparse table to answer queries efficiently. In a sparse table, we break queries in powers of 2.
Suppose we are asked to compute sum of elements from arr[i] to arr[i+12]. We do the following: // Use sum of 8 (or 23) elements table[i][3] = sum(arr[i], arr[i + 1], ... arr[i + 7]). // Use sum of 4 elements table[i+8][2] = sum(arr[i+8], arr[i+9], .. arr[i+11]). // Use sum of single element table[i + 12][0] = sum(arr[i + 12]). Our result is sum of above values.
Notice that it took only 4 actions to compute the result over a subarray of size 13.
Flowchart:
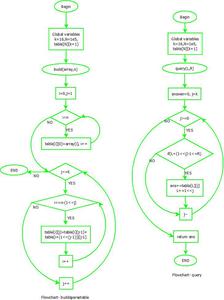Flowchart C++ // CPP program to find the sum in a given // range in an array using sparse table. #include <bits/stdc++.h> using namespace std; // Because 2^17 is larger than 10^5 const int k = 16; // Maximum value of array const int N = 1e5; // k + 1 because we need to access // table[r][k] long long table[N][k + 1]; // it builds sparse table. void buildSparseTable(int arr[], int n) { for (int i = 0; i < n; i++) table[i][0] = arr[i]; for (int j = 1; j <= k; j++) for (int i = 0; i <= n - (1 << j); i++) table[i][j] = table[i][j - 1] + table[i + (1 << (j - 1))][j - 1]; } // Returns the sum of the elements in the range // L and R. long long query(int L, int R) { // boundaries of next query, 0-indexed long long answer = 0; for (int j = k; j >= 0; j--) { if (L + (1 << j) - 1 <= R) { answer = answer + table[L][j]; // instead of having L', we // increment L directly L += 1 << j; } } return answer; } // Driver program. int main() { int arr[] = { 3, 7, 2, 5, 8, 9 }; int n = sizeof(arr) / sizeof(arr[0]); buildSparseTable(arr, n); cout << query(0, 5) << endl; cout << query(3, 5) << endl; cout << query(2, 4) << endl; return 0; } // Java program to find the sum // in a given range in an array // using sparse table. class GFG { // Because 2^17 is larger than 10^5 static int k = 16; // Maximum value of array static int N = 100000; // k + 1 because we need // to access table[r][k] static long table[][] = new long[N][k + 1]; // it builds sparse table. static void buildSparseTable(int arr[], int n) { for (int i = 0; i < n; i++) table[i][0] = arr[i]; for (int j = 1; j <= k; j++) for (int i = 0; i <= n - (1 << j); i++) table[i][j] = table[i][j - 1] + table[i + (1 << (j - 1))][j - 1]; } // Returns the sum of the // elements in the range L and R. static long query(int L, int R) { // boundaries of next query, // 0-indexed long answer = 0; for (int j = k; j >= 0; j--) { if (L + (1 << j) - 1 <= R) { answer = answer + table[L][j]; // instead of having L', we // increment L directly L += 1 << j; } } return answer; } // Driver Code public static void main(String args[]) { int arr[] = { 3, 7, 2, 5, 8, 9 }; int n = arr.length; buildSparseTable(arr, n); System.out.println(query(0, 5)); System.out.println(query(3, 5)); System.out.println(query(2, 4)); } } // This code is contributed // by Kirti_Mangal // C# program to find the // sum in a given range // in an array using // sparse table. using System; class GFG { // Because 2^17 is // larger than 10^5 static int k = 16; // Maximum value // of array static int N = 100000; // k + 1 because we // need to access table[r,k] static long [,]table = new long[N, k + 1]; // it builds sparse table. static void buildSparseTable(int []arr, int n) { for (int i = 0; i < n; i++) table[i, 0] = arr[i]; for (int j = 1; j <= k; j++) for (int i = 0; i <= n - (1 << j); i++) table[i, j] = table[i, j - 1] + table[i + (1 << (j - 1)), j - 1]; } // Returns the sum of the // elements in the range // L and R. static long query(int L, int R) { // boundaries of next // query, 0-indexed long answer = 0; for (int j = k; j >= 0; j--) { if (L + (1 << j) - 1 <= R) { answer = answer + table[L, j]; // instead of having // L', we increment // L directly L += 1 << j; } } return answer; } // Driver Code static void Main() { int []arr = new int[]{3, 7, 2, 5, 8, 9}; int n = arr.Length; buildSparseTable(arr, n); Console.WriteLine(query(0, 5)); Console.WriteLine(query(3, 5)); Console.WriteLine(query(2, 4)); } } // This code is contributed by // Manish Shaw(manishshaw1) # Python3 program to find the sum in a given # range in an array using sparse table. # Because 2^17 is larger than 10^5 k = 16 # Maximum value of array n = 100000 # k + 1 because we need to access # table[r][k] table = [[0 for j in range(k+1)] for i in range(n)] # it builds sparse table def buildSparseTable(arr, n): global table, k for i in range(n): table[i][0] = arr[i] for j in range(1,k+1): for i in range(0,n-(1<<j)+1): table[i][j] = table[i][j-1] + \ table[i + (1 << (j - 1))][j - 1] # Returns the sum of the elements in the range # L and R. def query(L, R): global table, k # boundaries of next query, 0 - indexed answer = 0 for j in range(k,-1,-1): if (L + (1 << j) - 1 <= R): answer = answer + table[L][j] # instead of having L ', we # increment L directly L+=1<<j return answer # Driver program if __name__ == '__main__': arr = [3, 7, 2, 5, 8, 9] n = len(arr) buildSparseTable(arr, n) print(query(0,5)) print(query(3,5)) print(query(2,4)) # This code is contributed by # chaudhary_19 (Mayank Chaudhary)
<script> // JavaScript program to find the sum in a given // range in an array using sparse table. // Because 2^17 is larger than 10^5 const k = 16; // Maximum value of array const N = 1e5; // k + 1 because we need to access // table[r][k] const table = new Array(N).fill(0).map(() => new Array(k + 1).fill(0)); // it builds sparse table. function buildSparseTable(arr, n) { for (let i = 0; i < n; i++) table[i][0] = arr[i]; for (let j = 1; j <= k; j++) for (let i = 0; i <= n - (1 << j); i++) table[i][j] = table[i][j - 1] + table[i + (1 << (j - 1))][j - 1]; } // Returns the sum of the elements in the range // L and R. function query(L, R) { // boundaries of next query, 0-indexed let answer = 0; for (let j = k; j >= 0; j--) { if (L + (1 << j) - 1 <= R) { answer = answer + table[L][j]; // instead of having L', we // increment L directly L += 1 << j; } } return answer; } // Driver program. let arr = [ 3, 7, 2, 5, 8, 9 ]; let n = arr.length; buildSparseTable(arr, n); document.write(query(0, 5) + "<br>"); document.write(query(3, 5) + "<br>"); document.write(query(2, 4) + "<br>"); // This code is contributed by Manoj. </script> Output:
34 22 15
This algorithm for answering queries with Sparse Table works in O(k), which is O(log(n)) because we choose minimal k such that 2^k+1 > n.
Time complexity of sparse table construction : Outer loop runs in O(k), inner loop runs in O(n). Thus, in total we get O(n * k) = O(n * log(n))
Auxiliary Space: O(n*k), since n*k extra space has been taken.
Similar Reads
PreComputation Technique on Arrays Precomputation refers to the process of pre-calculating and storing the results of certain computations or data structures(array in this case) in advance, in order to speed up the execution time of a program. This can be useful in situations where the same calculations are needed multiple times, as
15 min read
Queries for the product of first N factorials Given Q[] queries where each query consists of an integer N, the task is to find the product of first N factorials for each of the query. Since the result could be large, compute it modulo 109 + 7.Examples: Input: Q[] = {4, 5} Output: 288 34560 Query 1: 1! * 2! * 3! * 4! = 1 * 2 * 6 * 24 = 288 Query
7 min read
Range sum queries without updates Given an array arr of integers of size n. We need to compute the sum of elements from index i to index j. The queries consisting of i and j index values will be executed multiple times.Examples: Input : arr[] = {1, 2, 3, 4, 5} i = 1, j = 3 i = 2, j = 4Output : 9 12 Input : arr[] = {1, 2, 3, 4, 5} i
6 min read
Range Queries for Frequencies of array elements Given an array of n non-negative integers. The task is to find frequency of a particular element in the arbitrary range of array[]. The range is given as positions (not 0 based indexes) in array. There can be multiple queries of given type. Examples: Input : arr[] = {2, 8, 6, 9, 8, 6, 8, 2, 11}; lef
13 min read
Count Primes in Ranges Given a 2d array queries[][] of size n, where each query queries[i] contain 2 elements [l, r], your task is to find the count of number of primes in inclusive range [l, r]Examples: Input: queries[][] = [ [1, 10], [5, 10], [11, 20] ]Output: 4 2 4Explanation: For query 1, number of primes in range [1,
12 min read
Check in binary array the number represented by a subarray is odd or even Given an array such that all its terms is either 0 or 1.You need to tell the number represented by a subarray a[l..r] is odd or even Examples : Input : arr = {1, 1, 0, 1} l = 1, r = 3 Output : odd number represented by arr[l...r] is 101 which 5 in decimal form which is odd Input : arr = {1, 1, 1, 1}
4 min read
GCDs of given index ranges in an Array Given an array arr[] of size N and Q queries of type {qs, qe} where qs and qe denote the starting and ending index of the query, the task is to find the GCD of all the numbers in the range. Examples: Input: arr[] = {2, 3, 60, 90, 50};Index Ranges: {1, 3}, {2, 4}, {0, 2}Output: GCDs of given ranges a
14 min read
Mean of range in array Given an array arr[] of n integers and q queries represented by an array queries[][], where queries[i][0] = l and queries[i][1] = r. For each query, the task is to calculate the mean of elements in the range l to r and return its floor value. Examples: Input: arr[] = [3, 7, 2, 8, 5] queries[][] = [[
12 min read
Difference Array | Range update query in O(1) Given an array arr[] and a 2D array opr[][], where each row represents an operation in the form [l, r, v]. For each operation, add v to all elements from index l to r in arr. Return the updated array after applying all operations.Examples : Input: arr[] = [2, 3, 5, 6, 7], opr[][] = [[2, 4, 2], [3, 4
15+ min read
Range sum query using Sparse Table We have an array arr[]. We need to find the sum of all the elements in the range L and R where 0 <= L <= R <= n-1. Consider a situation when there are many range queries. Examples: Input : 3 7 2 5 8 9 query(0, 5) query(3, 5) query(2, 4) Output : 34 22 15Note : array is 0 based indexed and q
8 min read