Breadth First Search or BFS for a Graph in Python

Breadth First Search (BFS) is a fundamental graph traversal algorithm. It begins with a node, then first traverses all its adjacent nodes. Once all adjacent are visited, then their adjacent are traversed.

• BFS is different from DFS in a way that closest vertices are visited before others. We mainly traverse vertices level by level.
• Popular graph algorithms like Dijkstra’s shortest path, Kahn’s Algorithm, and Prim’s algorithm are based on BFS.
• BFS itself can be used to detect cycle in a directed and undirected graph, find shortest path in an unweighted graph and many more problems.

Examples:

Input: adj = [[2,3,1], [0], [0,4], [0], [2]]
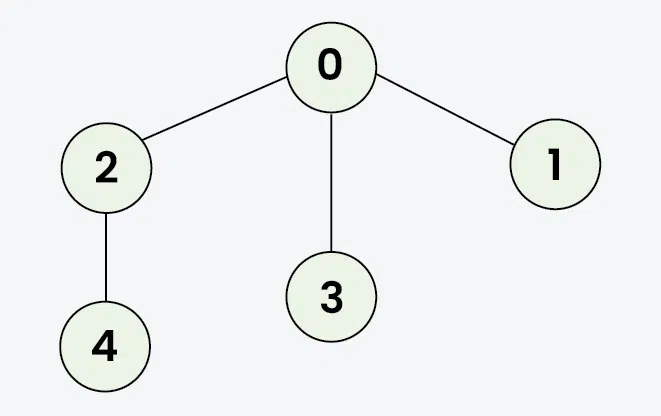Output: [0, 2, 3, 1, 4]
Explanation: Starting from 0, the BFS traversal will follow these steps:
Visit 0 → Output: 0
Visit 2 (first neighbor of 0) → Output: 0, 2
Visit 3 (next neighbor of 0) → Output: 0, 2, 3
Visit 1 (next neighbor of 0) → Output: 0, 2, 3,
Visit 4 (neighbor of 2) → Final Output: 0, 2, 3, 1, 4

Input: adj = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]
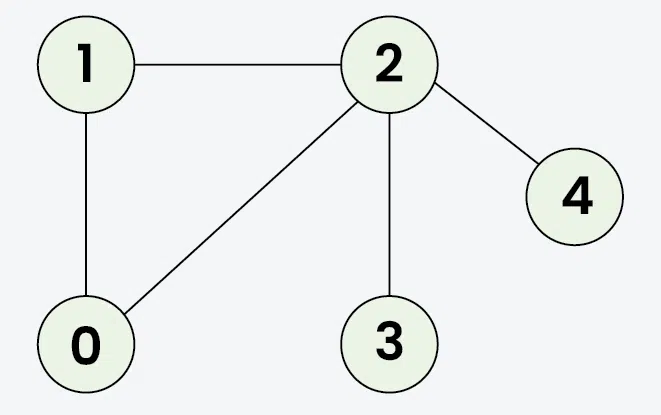Output: [0, 1, 2, 3, 4]
Explanation: Starting from 0, the BFS traversal proceeds as follows:
Visit 0 → Output: 0
Visit 1 (the first neighbor of 0) → Output: 0, 1
Visit 2 (the next neighbor of 0) → Output: 0, 1, 2
Visit 3 (the first neighbor of 2 that hasn’t been visited yet) → Output: 0, 1, 2, 3
Visit 4 (the next neighbor of 2) → Final Output: 0, 1, 2, 3, 4

Input: adj = [[1], [0, 2, 3], [1], [1, 4], [3]]
Output: [0, 1, 2, 3, 4]
Explanation: Starting the BFS from vertex 0:
Visit vertex 0 → Output: [0]
Visit vertex 1 (first neighbor of 0) → Output: [0, 1]
Visit vertex 2 (first unvisited neighbor of 1) → Output: [0, 1, 2]
Visit vertex 3 (next neighbor of 1) → Output: [0, 1, 2, 3]
Visit vertex 4 (neighbor of 3) → Final Output: [0, 1, 2, 3, 4]

BFS from a Given Source

The algorithm starts from a given source and explores all reachable vertices from the given source. It is similar to the Breadth-First Traversal of a tree. Like tree, we begin with the given source (in tree, we begin with root) and traverse vertices level by level using a queue data structure. The only catch here is that, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a Boolean visited array.

Follow the below given approach:

1. Initialization: Enqueue the given source vertex into a queue and mark it as visited.
2. Exploration: While the queue is not empty:
   • Dequeue a node from the queue and visit it (e.g., print its value).
   • For each unvisited neighbor of the dequeued node:
   • Enqueue the neighbor into the queue.
   • Mark the neighbor as visited.
3. Termination: Repeat step 2 until the queue is empty.

Code Implementation of BFS Python

Following are the implementations of simple Breadth First Traversal from a given source. The implementation uses adjacency list representation of graphs. STL\'s list container is used to store lists of adjacent nodes and a queue of nodes needed for BFS traversal.

from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # Default dictionary to store graph self.graph = defaultdict(list) # Function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print(s, end=" ") # Get all adjacent vertices of the # dequeued vertex s. # If an adjacent has not been visited, # then mark it visited and enqueue it for i in self.graph[s]: if not visited[i]: queue.append(i) visited[i] = True # Driver code if __name__ == '__main__': # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print("Following is Breadth First Traversal" " (starting from vertex 2)") g.BFS(2) 

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1 

Time Complexity : O(V+E), where V is the number of vertices in graph and E is the number of edges
Auxiliary Space: O(V)

Please refer complete article on Breadth First Search or BFS for a Graph for more details!