Vectorization in NumPy with Practical Examples

Vectorization in NumPy refers to applying operations on entire arrays without using explicit loops. These operations are internally optimized using fast C/C++ implementations, making numerical computations more efficient and easier to write.

Why Vectorization Matters?

Vectorization is important because it:

• Improves Performance: Eliminates Python-level loops and leverages fast low-level implementations.
• Produces Cleaner Code: Fewer lines, easier to maintain.
• Scales Better: Can efficiently handle large scientific data and machine learning workloads.

Examples of Vectorization

Example 1: Add a number to each element

Performs element-wise addition across the entire array without using loops, making the operation fast and efficient.

import numpy as np a1 = np.array([2, 4, 6, 8, 10]) num = 2 res = a1 + num print(res) 

[ 4 6 8 10 12] 

Example 2: Adding Two Arrays Element-wise

Performs element-wise addition of two NumPy arrays.

import numpy as np a1 = np.array([1, 2, 3]) a2 = np.array([4, 5, 6]) res = a1 + a2 print(res) 

[5 7 9] 

Example 3: Element-Wise Scalar Multiplication

Multiplies each element in the array by a constant value using fast vectorized array operations instead of loops.

import numpy as np a1 = np.array([1, 2, 3, 4]) res = a1 * 2 print(res) 

[2 4 6 8] 

Example 4: Logical Operations on Arrays

Logical operations such as comparisons can be applied directly to arrays.

import numpy as np a1 = np.array([10, 20, 30]) res = a1 > 15 print(res) 

[False True True] 

Explanation: Performs element-wise comparison, returning a boolean array indicating which elements are greater than 15.

Example 5: Matrix Operations Using Vectorization

NumPy supports vectorized matrix operations like dot products and matrix multiplications using functions such as np.dot and @.

import numpy as np a1= np.array([[1, 2], [3, 4]]) a2 = np.array([[5, 6], [7, 8]]) res = np.dot(a1, a2) print(res) 

[[19 22] [43 50]] 

Explanation: Performs matrix multiplication (dot product) between a1 and a2.

Example 6: Applying Custom Functions Using np.vectorize()

np.vectorize applies a custom function element-wise to a NumPy array, e.g., computing x² + 2x + 1 for each element efficiently.

import numpy as np a1 = np.array([1, 2, 3, 4]) vec = np.vectorize(lambda x: x**2 + 2*x + 1) res = vec(a1) print(res) 

[ 4 9 16 25] 

Explanation: Performs the operation x**2+2*x+1 element-wise on the array a1 using NumPy’s vectorized arithmetic.

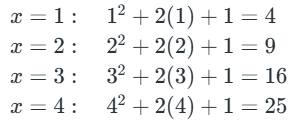
Example 7: Vectorized Aggregation Operations

Operations like sum, mean, max are optimized with much faster than the traditional Python approach of looping through elements.

import numpy as np a1 = np.array([1, 2, 3]) r1 = a1.sum() r2= a1.mean() print(r1) print(r2) 

6 2.0 

Explanation: Calculates the sum (r1) and mean (r2) of all elements in the array a1 using NumPy’s vectorized aggregation functions.

Performance Comparison: Loop vs. Vectorization

When working with large datasets, performance matters. In Pandas and NumPy, vectorization is almost always faster than writing manual Python loops. This is because vectorized operations are executed in optimized C code internally, while Python loops run line-by-line in Python (much slower).

Example: We will create a large NumPy array and apply the same operation (multiply each element by 2) using both:

• For Loop (Python-level)
• Vectorized Operation (NumPy-level)

import numpy as np import time arr = np.arange(1_000_000) # Loop t1 = time.time() loop_res = [x * 2 for x in arr] t2 = time.time() # Vectorized t3 = time.time() vec_res = arr * 2 t4 = time.time() print("Loop Time:", t2 - t1) print("Vectorized Time:", t4 - t3) 

Loop Time: 0.14799761772155762 Vectorized Time: 0.04310011863708496 

Explanation:

• arr = np.arange(1_000_000): Creates a NumPy array with 1 million numbers.
• Loop method: [x * 2 for x in arr] processes each element one-by-one in Python, which is slow and t2 - t1 measures how long the loop took.
• Vectorized method: arr * 2 uses fast optimized C-level operations inside NumPy and t4 - t3 measures how fast vectorization is.

Vectorization is significantly faster because operations happen in optimized low-level code instead of Python's slow element-by-element loop.

Related Articles:

• NumPy Tutorial - Python Library
• Create your own universal function in NumPy