Merge Sort vs. Insertion Sort
Last Updated : 05 Aug, 2025
Pre-requisite: Merge Sort, Insertion Sort
Merge Sort: is an external algorithm based on divide and conquer strategy. In this sorting:
- The elements are split into two sub-arrays (n/2) again and again until only one element is left.
- Merge sort uses additional storage for sorting the auxiliary array.
- Merge sort uses three arrays where two are used for storing each half, and the third external one is used to store the final sorted list by merging the other two and each array is then sorted recursively.
- At last, all sub-arrays are merged to make it ‘n’ element size of the array.
Below is the image to illustrate Merge Sort:
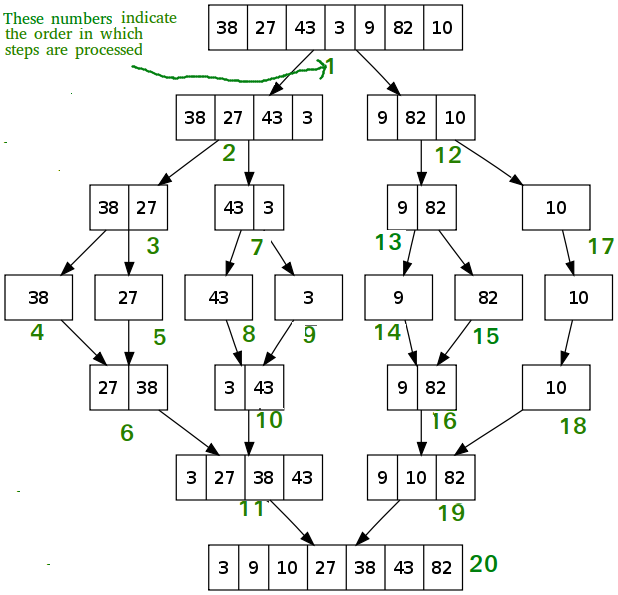
Insertion Sort is a sorting algorithm in which elements are taken from an unsorted item, inserting it in sorted order in front of the other items, and repeating until all items are in order. The algorithm is simple to implement and usually consists of two loops: an outer loop to pick items and an inner loop to iterate through the array. It works on the principle of sorting playing cards in our hands.
Below is the image to illustrate Insertion Sort:

Difference between Merge sort and Insertion sort:
- Time Complexity: In Merge Sort the Worst Case: O(N*log N), Average Case: O(N*log N), and Best Case: O(N*log N),
whereas
In Insertion Sort the Worst Case: O(N2), Average Case: O(N2), and Best Case: O(N). - Space Complexity: Merge sort being recursive takes up the auxiliary space complexity of O(N) hence it cannot be preferred over the place where memory is a problem,
whereas
In Insertion sort only takes O(1) auxiliary space complexity. It sorts the entire array just by using an extra variable. - Datasets: Merge Sort is preferred for huge data sets. It happens to compare all the elements present in the array hence is not much helpful for small datasets,
whereas
Insertion Sort is preferred for fewer elements. It becomes fast when data is already sorted or nearly sorted because it skips the sorted values. - Efficiency: Considering average time complexity of both algorithm we can say that Merge Sort is efficient in terms of time and Insertion Sort is efficient in terms of space.
- Sorting Method: The merge sort is an external sorting method in which the data that is to be sorted cannot be accommodated in the memory and needed auxiliary memory for sorting,
whereas
Insertion sort is based on the idea that one element from the input elements is consumed in each iteration to find its correct position i.e., the position to which it belongs in a sorted array. - Stability: Merge sort is stable as two elements with equal value appear in the same order in sorted output as they were in the input unsorted array,
whereas
Insertion sort takes O(N2) time on both data structures(Array and Linked list). If the CPU has an efficient memory block move function then the array may be quicker. Otherwise, there probably isn't that much of a time difference.
MERGE SORT PROGRAM:
C++ #include <iostream> using namespace std; void merge(int arr[], int l, int m, int r) { int i, j, k; int n1 = m - l + 1; int n2 = r - m; int L[n1], R[n2]; for (i = 0; i < n1; i++) L[i] = arr[l + i]; for (j = 0; j < n2; j++) R[j] = arr[m + 1+ j]; i = 0; j = 0; k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } while (i < n1) { arr[k] = L[i]; i++; k++; } while (j < n2) { arr[k] = R[j]; j++; k++; } } void mergeSort(int arr[], int l, int r) { if (l < r) { int m = l+(r-l)/2; mergeSort(arr, l, m); mergeSort(arr, m+1, r); merge(arr, l, m, r); } } void printArray(int A[], int size) { int i; for (i=0; i < size; i++) cout << A[i] << " "; cout << endl; } int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int arr_size = sizeof(arr)/sizeof(arr[0]); cout << "Given array is \n"; printArray(arr, arr_size); mergeSort(arr, 0, arr_size - 1); cout << "\nSorted array is \n"; printArray(arr, arr_size); return 0; } #include <stdio.h> void merge(int arr[], int l, int m, int r) { int i, j, k; int n1 = m - l + 1; int n2 = r - m; int L[n1], R[n2]; for (i = 0; i < n1; i++) L[i] = arr[l + i]; for (j = 0; j < n2; j++) R[j] = arr[m + 1+ j]; i = 0; j = 0; k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } while (i < n1) { arr[k] = L[i]; i++; k++; } while (j < n2) { arr[k] = R[j]; j++; k++; } } void mergeSort(int arr[], int l, int r) { if (l < r) { int m = l+(r-l)/2; mergeSort(arr, l, m); mergeSort(arr, m+1, r); merge(arr, l, m, r); } } void printArray(int A[], int size) { int i; for (i=0; i < size; i++) printf("%d ", A[i]); printf("\n"); } int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int arr_size = sizeof(arr)/sizeof(arr[0]); printf("Given array is \n"); printArray(arr, arr_size); mergeSort(arr, 0, arr_size - 1); printf("\nSorted array is \n"); printArray(arr, arr_size); return 0; } //This code is contributed snehalsalokhe class MergeSort { // marge array void merge(int arr[], int l, int m, int r) { int i, j, k; int n1 = m - l + 1; int n2 = r - m; int L[] = new int[n1]; int R[] = new int[n2]; for (i = 0; i < n1; i++) L[i] = arr[l + i]; for (j = 0; j < n2; j++) R[j] = arr[m + 1+ j]; i = 0; j = 0; k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } while (i < n1) { arr[k] = L[i]; i++; k++; } while (j < n2) { arr[k] = R[j]; j++; k++; } } // marge sort devide function void mergeSort(int arr[], int l, int r) { if (l < r) { int m = l + (r - l) / 2; mergeSort(arr, l, m); mergeSort(arr, m + 1, r); merge(arr, l, m, r); } } // Print array void printArray(int arr[]) { int n = arr.length; for (int i = 0; i < n; i++) System.out.print(arr[i] + " "); System.out.println(); } // Drive code public static void main(String args[]) { int arr[] = {12, 11, 13, 5, 6, 7}; System.out.println("Given array is"); MergeSort ob = new MergeSort(); ob.printArray(arr); ob.mergeSort(arr, 0, arr.length - 1); System.out.println("\nSorted array is"); ob.printArray(arr); } } // This code is contributed by shivhack999 def merge(arr, l, m, r): n1 = m - l + 1 n2 = r - m L = [0] * n1 R = [0] * n2 for i in range(n1): L[i] = arr[l + i] for j in range(n2): R[j] = arr[m + 1 + j] i = 0 j = 0 k = l while i < n1 and j < n2: if L[i] <= R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 while i < n1: arr[k] = L[i] i += 1 k += 1 while j < n2: arr[k] = R[j] j += 1 k += 1 def merge_sort(arr, l, r): if l < r: m = l + (r - l) // 2 merge_sort(arr, l, m) merge_sort(arr, m + 1, r) merge(arr, l, m, r) def print_array(arr): for i in arr: print(i, end=" ") print() if __name__ == "__main__": arr = [12, 11, 13, 5, 6, 7] arr_size = len(arr) print("Given array is") print_array(arr) merge_sort(arr, 0, arr_size - 1) print("\nSorted array is") print_array(arr) # This code contributed by Siddhesh using System; class Program { static void Merge(int[] arr, int l, int m, int r) { int i, j, k; int n1 = m - l + 1; int n2 = r - m; int[] L = new int[n1]; int[] R = new int[n2]; for (i = 0; i < n1; i++) L[i] = arr[l + i]; for (j = 0; j < n2; j++) R[j] = arr[m + 1 + j]; i = 0; j = 0; k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } while (i < n1) { arr[k] = L[i]; i++; k++; } while (j < n2) { arr[k] = R[j]; j++; k++; } } static void MergeSort(int[] arr, int l, int r) { if (l < r) { int m = l + (r - l) / 2; MergeSort(arr, l, m); MergeSort(arr, m + 1, r); Merge(arr, l, m, r); } } static void Main(string[] args) { int[] arr = new int[] { 12, 11, 13, 5, 6, 7 }; int arrSize = arr.Length; Console.WriteLine("Given array is"); Console.WriteLine(string.Join(" ", arr)); MergeSort(arr, 0, arrSize - 1); Console.WriteLine("\nSorted array is"); Console.WriteLine(string.Join(" ", arr)); } } function merge(arr, l, m, r) { // Find sizes of two subarrays to be merged let n1 = m - l + 1; let n2 = r - m; // Create temporary arrays let L = new Array(n1); let R = new Array(n2); // Copy data to temporary arrays L[] and R[] for (let i = 0; i < n1; i++) L[i] = arr[l + i]; for (let j = 0; j < n2; j++) R[j] = arr[m + 1 + j]; // Merge the temporary arrays back into arr[l..r] let i = 0, j = 0, k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } // Copy the remaining elements of L[], if any while (i < n1) { arr[k] = L[i]; i++; k++; } // Copy the remaining elements of R[], if any while (j < n2) { arr[k] = R[j]; j++; k++; } } function mergeSort(arr, l, r) { if (l < r) { // Find the middle point let m = Math.floor(l + (r - l) / 2); // Sort first and second halves mergeSort(arr, l, m); mergeSort(arr, m + 1, r); // Merge the sorted halves merge(arr, l, m, r); } } let arr = [12, 11, 13, 5, 6, 7]; let arrSize = arr.length; console.log("Given array is"); console.log(arr.join(" ")); // Perform Merge Sort on the array mergeSort(arr, 0, arrSize - 1); console.log("\nSorted array is"); console.log(arr.join(" ")); OutputGiven array is 12 11 13 5 6 7 Sorted array is 5 6 7 11 12 13
INSERTION SORT PROGRAM:
C++ #include<iostream> void insertionSort(int arr[], int n) { int i, key, j; for (i = 1; i < n; i++) { key = arr[i]; j = i - 1; while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = key; } } void printArray(int arr[], int n) { for (int i = 0; i < n; i++) std::cout << arr[i] << " "; std::cout << std::endl; } int main() { int arr[] = {12, 11, 13, 5, 6}; int n = sizeof(arr) / sizeof(arr[0]); std::cout << "Given array is" << std::endl; printArray(arr, n); insertionSort(arr, n); std::cout << "\nSorted array is" << std::endl; printArray(arr, n); return 0; } #include<stdio.h> void insertionSort(int arr[], int n) { int i, key, j; for (i = 1; i < n; i++) { key = arr[i]; j = i - 1; while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = key; } } void printArray(int arr[], int n) { int i; for (i = 0; i < n; i++) printf("%d ", arr[i]); printf("\n"); } int main() { int arr[] = {12, 11, 13, 5, 6}; int n = sizeof(arr)/sizeof(arr[0]); printf("Given array is \n"); printArray(arr, n); insertionSort(arr, n); printf("\nSorted array is \n"); printArray(arr, n); return 0; } public class InsertionSort { // Function to perform insertion sort on an array static void insertionSort(int arr[], int n) { int i, key, j; for (i = 1; i < n; i++) { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1] that are greater than key // to one position ahead of their current position while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = key; } } // Function to print an array static void printArray(int arr[], int n) { for (int i = 0; i < n; i++) System.out.print(arr[i] + " "); System.out.println(); } // Driver method to test the above public static void main(String args[]) { int arr[] = {12, 11, 13, 5, 6}; int n = arr.length; System.out.println("Given array is:"); printArray(arr, n); insertionSort(arr, n); System.out.println("\nSorted array is:"); printArray(arr, n); } } // Contributed by Siddhesh def insertion_sort(arr): for i in range(1, len(arr)): key = arr[i] j = i - 1 while j >= 0 and arr[j] > key: arr[j + 1] = arr[j] j = j - 1 arr[j + 1] = key def print_array(arr): for i in arr: print(i, end=" ") print() if __name__ == "__main__": arr = [12, 11, 13, 5, 6] n = len(arr) print("Given array is") print_array(arr) insertion_sort(arr) print("\nSorted array is") print_array(arr) # This code contributed by Siddhesh using System; public class InsertionSortExample { // Function to perform Insertion Sort on an array of integers static void InsertionSort(int[] arr, int n) { int i, key, j; for (i = 1; i < n; i++) { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1] that are greater than key // to one position ahead of their current position // Finding the correct position for arr[i] in the sorted part of the array while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; j = j - 1; } // Placing arr[i] at its correct position in the sorted array arr[j + 1] = key; } } // Function to print the elements of an array static void PrintArray(int[] arr, int n) { for (int i = 0; i < n; i++) { Console.Write(arr[i] + " "); } Console.WriteLine(); } public static void Main(string[] args) { int[] arr = { 12, 11, 13, 5, 6 }; int n = arr.Length; Console.WriteLine("Given array is:"); PrintArray(arr, n); // Perform Insertion Sort on the array InsertionSort(arr, n); Console.WriteLine("\nSorted array is:"); PrintArray(arr, n); } } // Function to perform insertion sort on an array function insertionSort(arr) { let n = arr.length; for (let i = 1; i < n; i++) { let key = arr[i]; let j = i - 1; // Move elements that are greater than key to one position ahead // of their current position while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = key; } } // Function to print an array function printArray(arr) { for (let i = 0; i < arr.length; i++) { process.stdout.write(arr[i] + " "); } console.log(); } // Test the insertion sort algorithm let arr = [12, 11, 13, 5, 6]; console.log("Given array is:"); printArray(arr); insertionSort(arr); console.log("\nSorted array is:"); printArray(arr); OutputGiven array is 12 11 13 5 6 Sorted array is 5 6 11 12 13
Tabular Representation:
|
| Worst Case Complexity | O(N*log N) | O(N2) |
| Average Case Complexity | O(N*log N) | O(N2) |
| Best Case Complexity | O(N*log N) | O(N) |
| Auxiliary Space Complexity | O(N) | O(1) |
| Works well on | On huge dataset. | On small dataset. |
| Efficiency | Comparatively Efficient. | Comparatively Inefficient. |
| Inplace Sorting | No | Yes |
| Algorithm Paradigm | Divide and Conquer | Incremental Approach |
| Uses | It is used for sorting linked list in O(N*log N), for Inversion Count problem, External sorting, etc. | It is used when number of elements is small. It can also be useful when input array is almost sorted, only few elements are misplaced in complete big array. |
Explore
DSA Fundamentals
Data Structures
Algorithms
Advanced
Interview Preparation
Practice Problem
My Profile