Classifying data using Support Vector Machines(SVMs) in Python
Last Updated : 02 Aug, 2025
Support Vector Machines (SVMs) are supervised learning algorithms widely used for classification and regression tasks. They can handle both linear and non-linear datasets by identifying the optimal decision boundary (hyperplane) that separates classes with the maximum margin. This improves generalization and reduces misclassification.
Core Concepts
- Hyperplane : The decision boundary separating classes. It is a line in 2D, a plane in 3D or a hyperplane in higher dimensions.
- Support Vectors : The data points closest to the hyperplane. These points directly influence its position and orientation.
- Margin : The distance between the hyperplane and the nearest support vectors from each class. SVMs aim to maximize this margin for better robustness and generalization.
- Regularization Parameter (C) : Controls the trade-off between maximizing the margin and minimizing classification errors. A high value of C prioritizes correct classification but may overfit. A low value of C prioritizes a larger margin but may underfit.
Optimization Objective
SVMs solve a constrained optimization problem with two main goals:
- Maximize the margin between classes for better generalization.
- Minimize classification errors on the training data, controlled by the parameter
C.
The Kernel Trick
Real-world data is rarely linearly separable. The kernel trick elegantly solves this by implicitly mapping data into higher-dimensional spaces where linear separation becomes possible, without explicitly computing the transformation.
Common Kernel Functions
- Linear Kernel: Ideal for linearly separable data, offers the fastest computation and serves as a reliable baseline.
- Polynomial Kernel: Models polynomial relationships with complexity controlled by degree d, allowing curved decision boundaries.
- Radial Basis Function (RBF) Kernel: Maps data to infinite-dimensional space, widely used for non-linear problems with parameter \gamma controlling influence of each sample.
- Sigmoid Kernel: Resembles neural network activation functions but is less common in practice due to limited effectiveness.
Implementing SVM Classification in Python
1. Importing Required Libraries
We will import required python libraries
- NumPy: Used for numerical operations.
- Matplotlib: Used for plotting graphs (can be used later for decision boundaries).
- load_breast_cancer: Loads the Breast Cancer Wisconsin dataset from scikit-learn.
- StandardScaler: Standardizes features by removing the mean and scaling to unit variance.
- SVC: Support Vector Classifier from scikit-learn.
Python import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import load_breast_cancer from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.svm import SVC from sklearn.metrics import accuracy_score, classification_report
2. Loading the Dataset
We will load the dataset and select only two features for visualization:
- load_breast_cancer(): Returns a dataset with 569 samples and 30 features.
- data.data[:, [0, 1]]: Selects only two features (mean radius and mean texture) for simplicity and visualization.
- data.target: Contains the binary target labels (malignant or benign).
Python data = load_breast_cancer() X = data.data[:, [0, 1]] y = data.target
3. Splitting the Data
We will split the dataset into training and test sets:
- train_test_split: splits data into training (80%) and test (20%) sets
- random_state=42: ensures reproducibility
Python X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42 )
4. Scale the Features
We will scale the features so that they are standardized:
- StandardScaler – standardizes data by removing mean and scaling to unit variance
- fit_transform() – fits the scaler to training data and transforms it
- transform() – applies the same scaling to test data
Python scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test)
5. Train the SVM Classifier
We will train the Support Vector Classifier:
- SVC: creates an SVM classifier with a specified kernel
- kernel='linear': uses a linear kernel for classification
- C=1.0: regularization parameter to control margin vs misclassification
- fit(): trains the classifier on scaled training data
Python svm_classifier = SVC(kernel='linear', C=1.0, random_state=42) svm_classifier.fit(X_train_scaled, y_train)
6. Evaluate the Model
We will predict labels and evaluate model performance:
- predict(): makes predictions on test data
- accuracy_score(): calculates prediction accuracy
- classification_report(): shows precision, recall and F1-score for each class
Python y_pred = svm_classifier.predict(X_test_scaled) print(f"Accuracy: {accuracy_score(y_test, y_pred):.2f}") print(classification_report(y_test, y_pred, target_names=data.target_names)) Output:
 SVM - output
SVM - outputVisualizing the Decision Boundary
We will plot the decision boundary for the trained SVM model:
- np.meshgrid() : creates a grid of points across the feature space
- predict() : classifies each point in the grid using the trained model
- plt.contourf() : fills regions based on predicted classes
- plt.scatter() : plots the actual data points
Python def plot_decision_boundary(X, y, model, scaler): h = 0.02 # Step size for mesh x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) # Predict on mesh points Z = model.predict(scaler.transform(np.c_[xx.ravel(), yy.ravel()])) Z = Z.reshape(xx.shape) # Plot decision boundary and data points plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.3) plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, edgecolors='k') plt.xlabel(data.feature_names[0]) plt.ylabel(data.feature_names[1]) plt.title('SVM Decision Boundary') plt.show() plot_decision_boundary(X_train, y_train, svm_classifier, scaler) Output:
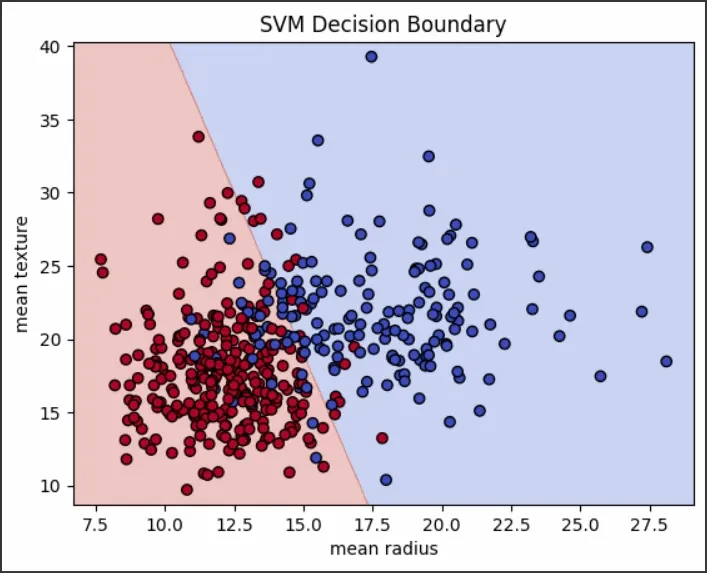 SVM decision boundary
SVM decision boundaryWhy Use SVMs
SVMs work best when the data has clear margins of separation, when the feature space is high-dimensional (such as text or image classification) and when datasets are moderate in size so that quadratic optimization remains feasible.
Advantages
- Performs well in high-dimensional spaces.
- Relies only on support vectors, which speeds up predictions.
- Can be used for both binary and multi-class classification.
Limitations
- Computationally expensive for large datasets with time complexity O(n²)–O(n³).
- Requires feature scaling and careful hyperparameter tuning.
- Sensitive to outliers and class imbalance, which may skew the decision boundary.
Support Vector Machines are a robust choice for classification, especially when classes are well-separated. By maximizing the margin around the decision boundary, they deliver strong generalization performance across diverse datasets.
For Large Datasets
- Use LinearSVC for linear kernels (faster than SVC with linear kernel)
- Consider SGDClassifier with hinge loss as an alternative
Memory Management
- Use probability = False if you don't need probability estimates
- Consider incremental learning for very large datasets
- Use sparse data formats when applicable
Preprocessing Best Practices
- Always scale features before training
- Remove or handle outliers appropriately
- Consider feature engineering for better separability
- Use dimensionality reduction for high-dimensional sparse data
Explore
Machine Learning Basics
Python for Machine Learning
Feature Engineering
Supervised Learning
Unsupervised Learning
Model Evaluation and Tuning
Advanced Techniques
Machine Learning Practice
My Profile