Implementation of Deque using circular array

Deque or Double Ended Queue is a generalized version of the Queue data structure that allows insert and delete at both ends.

Operations on Deque: 

Mainly the following four basic operations are performed on queue: 

• insertFront(): Adds an item at the front of Deque.
• insertRear(): Adds an item at the rear of Deque. 
• deleteFront(): Deletes an item from front of Deque. 
• deleteRear(): Deletes an item from rear of Deque.

In addition to above operations, following operations are also supported 

• frontEle(): Gets the front item from queue. 
• RearEle(): Gets the last item from queue. 

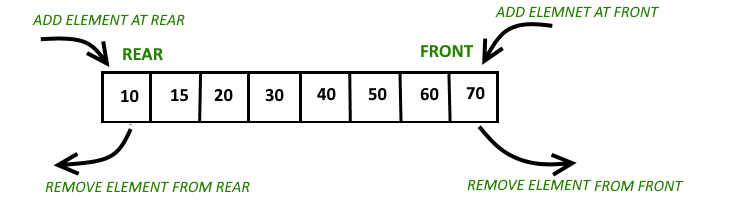
Circular array implementation of Deque

For implementing deque, we need to keep track of two indices, front and rear. We enqueue(push) an item at the rear or the front end of the deque and dequeue(pop) an item from both the rear and the front end. 

Working: 

• Create an array 'arr' of size n to store the elements. 
• Initialize the front and size: front is initialized to 0, and size to 0, indicating the deque is initially empty.
• Inserting elements: When an element is inserted at the front, we move the front index circularly. Similarly, inserting at the rear calculates the rear index using the formula (front + size) % capacity.
• Removing elements: Deleting from the front decreases the front index, and deleting from the rear calculates the rear index using (front + size - 1) % capacity to remove elements accordingly.

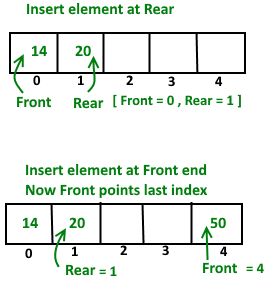
Insert Elements at the Rear end of Deque:

• First we check deque if Full or Not
• If size == capacity
  return (deque is full)
• Else calculate rear index: rear = (front + size) % capacity
• Insert element into arr[rear] = key
• Increment size by 1
  size++

Insert Elements at the Front end  of Deque:

• First we check deque if Full or Not
• IF size == capacity
  return (deque is full)
• Else calculate front index: front = (front - 1 + capacity) % capacity
• Insert element into arr[front] = key
• Increment size by 1
  size++

Delete Element From Rear end of Deque

• First we check deque if Empty or Not
• IF size == 0
  return (deque is empty)
• Else calculate rear index: rear = (front + size - 1) % capacity
• Store the element to be deleted: res = arr[rear]
• Decrement size by 1
  size--
• Return the deleted element
  return res

Delete Element From the Front end of Deque

• First we check deque if Empty or Not
• IF size == 0
  return (deque is empty)
• Store the front element: res = arr[front]
• Move front index circularly: front = (front + 1) % capacity
• Decrement size by 1
  size--
• Return the deleted element
  return res

Below is the implementation of the above methods: 

// C++ implementation of De-queue using circular array #include <iostream> using namespace std; class MyDeque {  private:  int *arr;  int front, size, capacity;  public:  // Constructor to initialize the deque  MyDeque(int c) {  arr = new int[c];  capacity = c;  size = 0;  front = 0;  }  // Delete element from the front  int deleteFront() {  // Empty deque  if (size == 0)  return -1;  int res = arr[front];  // Move front index circularly  front = (front + 1) % capacity;  size--;  return res;  }  // Insert element at the front  void insertFront(int x) {  // Full deque  if (size == capacity)  return;  // Move front index circularly  front = (front - 1 + capacity) % capacity;  arr[front] = x;  size++;  }  // Insert element at the rear  void insertRear(int x) {  // Full deque  if (size == capacity)  return;  // Calculate rear index  int rear = (front + size) % capacity;  arr[rear] = x;  size++;  }  // Delete element from the rear  int deleteRear() {  // Empty deque  if (size == 0)  return -1;  int rear = (front + size - 1) % capacity;  size--;  return arr[rear];  }  // Get the front element  int frontEle() {  return arr[front];  }  // Get the rear element  int rearEle() {  // Calculate rear index  int rear = (front + size - 1) % capacity;  return arr[rear];  } }; int main() {  // Create deque with capacity 4  MyDeque dq(4);  // Insert at rear  dq.insertRear(10);  cout << dq.frontEle() << " " << dq.rearEle() << endl;  // Insert at front  dq.insertFront(20);  cout << dq.frontEle() << " " << dq.rearEle() << endl;  dq.insertFront(30);  cout << dq.frontEle() << " " << dq.rearEle() << endl;  // Delete from rear  dq.deleteRear();  cout << dq.frontEle() << " " << dq.rearEle() << endl;  dq.insertRear(40);  cout << dq.frontEle() << " " << dq.rearEle() << endl;  dq.deleteRear();  cout << dq.frontEle() << " " << dq.rearEle() << endl;  return 0; } 

// Java implementation of De-queue using circular array class MyDeque {  private int[] arr;  private int front, size, capacity;  // Constructor to initialize the deque with a given  // capacity  public MyDeque(int c) {  arr = new int[c];  capacity = c;  size = 0;  front = 0;  }  // Delete element from the front  public int deleteFront() {  // Empty deque  if (size == 0)  return -1;  int res = arr[front];  // Move front index circularly  front = (front + 1) % capacity;  size--;  return res;  }  // Insert element at the front  public void insertFront(int x) {  // Full deque  if (size == capacity)  return;  // Move front index circularly  front = (front - 1 + capacity) % capacity;  arr[front] = x;  size++;  }  // Insert element at the rear  public void insertRear(int x) {  // Full deque  if (size == capacity)  return;  // Calculate rear index  int rear = (front + size) % capacity;  arr[rear] = x;  size++;  }  // Delete element from the rear  public int deleteRear() {  // Empty deque  if (size == 0)  return -1;  // Calculate rear index  int rear = (front + size - 1) % capacity;  size--;  return arr[rear];  }  // Get the front element  public int frontEle() { return arr[front]; }  // Get the rear element  public int rearEle() {  // Calculate rear index  int rear = (front + size - 1) % capacity;  return arr[rear];  } } class GfG {  public static void main(String[] args) {  // Create deque with capacity 4  MyDeque dq = new MyDeque(4);  // Insert at rear  dq.insertRear(10);  System.out.println(dq.frontEle() + " "  + dq.rearEle());  // Insert at front  dq.insertFront(20);  System.out.println(dq.frontEle() + " "  + dq.rearEle());  dq.insertFront(30);  System.out.println(dq.frontEle() + " "  + dq.rearEle());  // Delete from rear  dq.deleteRear();  System.out.println(dq.frontEle() + " "  + dq.rearEle());  dq.insertRear(40);  System.out.println(dq.frontEle() + " "  + dq.rearEle());  dq.deleteRear();  System.out.println(dq.frontEle() + " "  + dq.rearEle());  } } 

# Python implementation of De-queue using circular array class MyDeque: # Constructor to initialize the deque with a given capacity def __init__(self, c): self.l = [None] * c self.cap = c self.size = 0 self.front = 0 # Delete element from the front def deleteFront(self): # Return None if deque is empty if self.size == 0: return None else: res = self.l[self.front] # Move front index circularly self.front = (self.front + 1) % self.cap self.size -= 1 return res # Insert element at the front def insertFront(self, x): # Return if deque is full if self.size == self.cap: return else: # Move front index circularly self.front = (self.front - 1 + self.cap) % self.cap self.l[self.front] = x self.size += 1 # Insert element at the rear def insertRear(self, x): # Return if deque is full if self.size == self.cap: return # Calculate rear index new_rear = (self.front + self.size) % self.cap self.l[new_rear] = x self.size += 1 # Delete element from the rear def deleteRear(self): sz = self.size # Return None if deque is empty if sz == 0: return None else: # Calculate rear index rear = (self.front + sz - 1) % self.cap self.size -= 1 return self.l[rear] # Get the front element def frontEle(self): return self.l[self.front] # Get the rear element def rearEle(self): # Calculate rear index rear = (self.front + self.size - 1) % self.cap return self.l[rear] if __name__ == "__main__": # Create deque with capacity 4 dq = MyDeque(4) # Insert at rear dq.insertRear(10) print(dq.frontEle(), dq.rearEle()) # Insert at front dq.insertFront(20) print(dq.frontEle(), dq.rearEle()) dq.insertFront(30) print(dq.frontEle(), dq.rearEle()) # Delete from rear dq.deleteRear() print(dq.frontEle(), dq.rearEle()) dq.insertRear(40) print(dq.frontEle(), dq.rearEle()) dq.deleteRear() print(dq.frontEle(), dq.rearEle()) 

// C# implementation of De-queue using circular array using System; class MyDeque {  private int[] arr;  private int front, size, capacity;  // Constructor to initialize the deque with a given  // capacity  public MyDeque(int c) {  arr = new int[c];  capacity = c;  size = 0;  front = 0;  }  // Delete element from the front  public int deleteFront() {  // Empty deque  if (size == 0)  return -1;  int res = arr[front];  // Move front index circularly  front = (front + 1) % capacity;  size--;  return res;  }  // Insert element at the front  public void insertFront(int x) {  // Full deque  if (size == capacity)  return;  // Move front index circularly  front = (front - 1 + capacity) % capacity;  arr[front] = x;  size++;  }  // Insert element at the rear  public void insertRear(int x) {  // Full deque  if (size == capacity)  return;  // Calculate rear index  int rear = (front + size) % capacity;  arr[rear] = x;  size++;  }  // Delete element from the rear  public int deleteRear() {  // Empty deque  if (size == 0)  return -1;  // Calculate rear index  int rear = (front + size - 1) % capacity;  size--;  return arr[rear];  }  // Get the front element  public int frontEle() { return arr[front]; }  // Get the rear element  public int rearEle() {  int rear = (front + size - 1) % capacity;  return arr[rear];  } } class GfG {  static void Main() {  // Create deque with capacity 4  MyDeque dq = new MyDeque(4);  // Insert at rear  dq.insertRear(10);  Console.WriteLine(dq.frontEle() + " "  + dq.rearEle());  // Insert at front  dq.insertFront(20);  Console.WriteLine(dq.frontEle() + " "  + dq.rearEle());  dq.insertFront(30);  Console.WriteLine(dq.frontEle() + " "  + dq.rearEle());  // Delete from rear  dq.deleteRear();  Console.WriteLine(dq.frontEle() + " "  + dq.rearEle());  dq.insertRear(40);  Console.WriteLine(dq.frontEle() + " "  + dq.rearEle());  dq.deleteRear();  Console.WriteLine(dq.frontEle() + " "  + dq.rearEle());  } } 

// Javascript implementation of De-queue using circular // array class MyDeque {  constructor(c) {  this.arr = new Array(c);  this.capacity = c;  this.size = 0;  this.front = 0;  }  // Delete element from the front  deleteFront() {  // Empty deque  if (this.size === 0)  return -1;  const res = this.arr[this.front];  // Move front index circularly  this.front = (this.front + 1) % this.capacity;  this.size--;  return res;  }  // Insert element at the front  insertFront(x) {  // Full deque  if (this.size === this.capacity)  return;  // Move front index circularly  this.front = (this.front - 1 + this.capacity)  % this.capacity;  this.arr[this.front] = x;  this.size++;  }  // Insert element at the rear  insertRear(x) {  // Full deque  if (this.size === this.capacity)  return;  // Calculate rear index  const rear  = (this.front + this.size) % this.capacity;  this.arr[rear] = x;  this.size++;  }  // Delete element from the rear  deleteRear() {  // Empty deque  if (this.size === 0)  return -1;  // Calculate rear index  const rear  = (this.front + this.size - 1) % this.capacity;  this.size--; // Decrease size  return this.arr[rear];  }  // Get the front element  frontEle() { return this.arr[this.front]; }  // Get the rear element  rearEle() {  const rear  = (this.front + this.size - 1) % this.capacity;  return this.arr[rear];  } } // Test case // Create deque with capacity 4 const dq = new MyDeque(4); // Insert at rear dq.insertRear(10); console.log(dq.frontEle(), dq.rearEle()); // Insert at front dq.insertFront(20); console.log(dq.frontEle(), dq.rearEle()); dq.insertFront(30); console.log(dq.frontEle(), dq.rearEle()); // Delete from rear dq.deleteRear(); console.log(dq.frontEle(), dq.rearEle()); dq.insertRear(40); console.log(dq.frontEle(), dq.rearEle()); dq.deleteRear(); console.log(dq.frontEle(), dq.rearEle()); 

10 10 20 10 30 10 30 20 30 40 30 20 

Time Complexity:

• insertFront(x): O(1)
• insertRear(x): O(1)
• deleteFront(): O(1)
• deleteRear(): O(1)
• frontEle(): O(1)
• rearEle(): O(1)

Auxiliary Space: O(n), where n is the size of the array for storing elements.