Activation functions in Neural Networks
Last Updated : 08 Oct, 2025
An activation function in a neural network is a mathematical function applied to the output of a neuron. It introduces non-linearity, enabling the model to learn and represent complex data patterns. Without it, even a deep neural network would behave like a simple linear regression model.
Activation functions decide whether a neuron should be activated based on the weighted sum of inputs and a bias term. They also make backpropagation possible by providing gradients for weight updates.
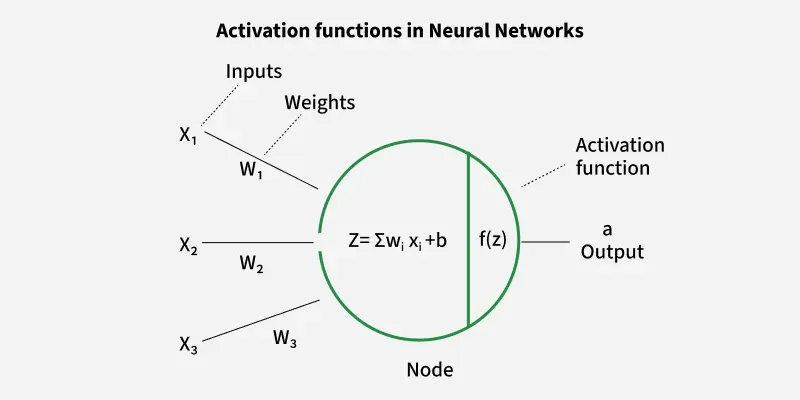 Activation Functions in neural Networks
Activation Functions in neural NetworksWhy Non-Linearity is Important
- Real-world data is rarely linearly separable.
- Non-linear functions allow neural networks to form curved decision boundaries, making them capable of handling complex patterns (e.g., classifying apples vs. bananas under varying colors and shapes).
- They ensure networks can model advanced problems like image recognition, NLP and speech processing.
Mathematical Example
Consider a neural network with:
- Inputs: i1, i2
- Hidden layer: neurons h1 and h2
- Output layer: one neuron (output)
- Weights: w1, w2, w3, w4, w5, w6
- Biases: b1 for hidden layer, b2 for output layer
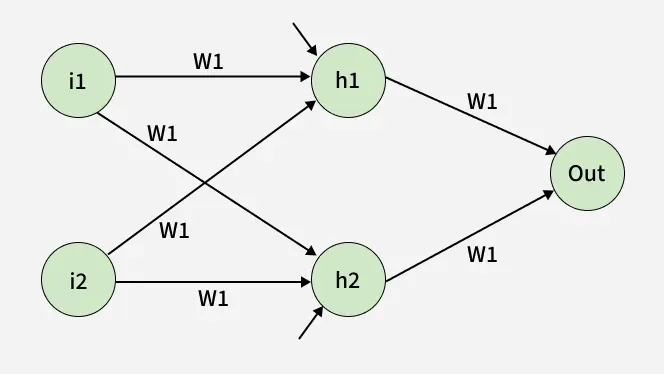 neural network
neural networkThe hidden layer outputs are:
{h_1} = i_1.w_1 + i_2.w_3 + b_1
{h_2} = i_1.w_2 + i_2.w_4 + b_2
The output before activation is:
\text{output} = h_1.w_5 + h_2.w_6 + \text{bias}
Without activation, these are linear equations.
To introduce non-linearity, we apply a sigmoid activation:
\sigma(x) = \frac{1}{1+e^{-x}}
\text{final output} = \sigma(h_1.w_5 + h_2.w_6 + \text{bias})
This gives the final output of the network after applying the sigmoid activation function in output layers, introducing the desired non-linearity.
Types of Activation Functions in Deep Learning
1. Linear Activation Function
Linear Activation Function resembles straight line define by y=x. No matter how many layers the neural network contains if they all use linear activation functions the output is a linear combination of the input.
- The range of the output spans from (-\infty \text{ to } + \infty).
- Linear activation function is used at just one place i.e. output layer.
- Using linear activation across all layers makes the network's ability to learn complex patterns limited.
Linear activation functions are useful for specific tasks but must be combined with non-linear functions to enhance the neural network’s learning and predictive capabilities.
 Linear Activation Function or Identity Function returns the input as the output
Linear Activation Function or Identity Function returns the input as the output2. Non-Linear Activation Functions
1. Sigmoid Function
Sigmoid Activation Function is characterized by 'S' shape. It is mathematically defined as A = \frac{1}{1 + e^{-x}}. This formula ensures a smooth and continuous output that is essential for gradient-based optimization methods.
- It allows neural networks to handle and model complex patterns that linear equations cannot.
- The output ranges between 0 and 1, hence useful for binary classification.
- The function exhibits a steep gradient when x values are between -2 and 2. This sensitivity means that small changes in input x can cause significant changes in output y which is critical during the training process.
 Sigmoid or Logistic Activation Function Graph
Sigmoid or Logistic Activation Function Graph2. Tanh Activation Function
Tanh function(hyperbolic tangent function) is a shifted version of the sigmoid, allowing it to stretch across the y-axis. It is defined as:
f(x) = \tanh(x) = \frac{2}{1 + e^{-2x}} - 1.
Alternatively, it can be expressed using the sigmoid function:
\tanh(x) = 2 \times \text{sigmoid}(2x) - 1
- Value Range: Outputs values from -1 to +1.
- Non-linear: Enables modeling of complex data patterns.
- Use in Hidden Layers: Commonly used in hidden layers due to its zero-centered output, facilitating easier learning for subsequent layers.
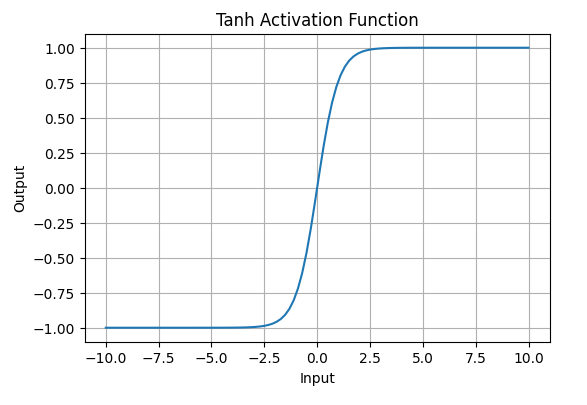 Tanh Activation Function
Tanh Activation Function3. ReLU (Rectified Linear Unit) Function
ReLU activation is defined by A(x) = \max(0,x), this means that if the input x is positive, ReLU returns x, if the input is negative, it returns 0.
- Value Range: [0, \infty), meaning the function only outputs non-negative values.
- Nature: It is a non-linear activation function, allowing neural networks to learn complex patterns and making backpropagation more efficient.
- Advantage over other Activation: ReLU is less computationally expensive than tanh and sigmoid because it involves simpler mathematical operations. At a time only a few neurons are activated making the network sparse making it efficient and easy for computation.
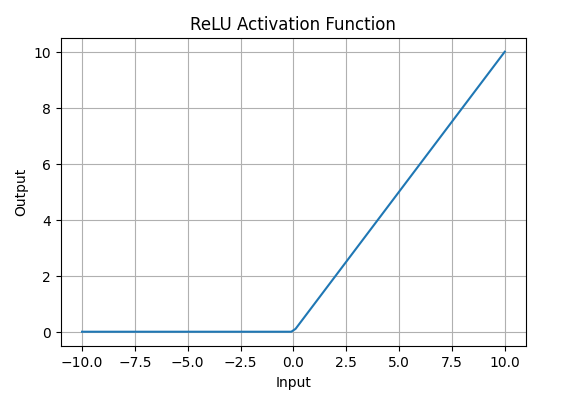 ReLU Activation Function
ReLU Activation Functiond) Leaky ReLU
f(x) = \begin{cases} x, & x > 0 \\ \alpha x, & x \leq 0 \end{cases}
- Leaky ReLU is similar to ReLU but allows a small negative slope (\alpha, e.g., 0.01) instead of zero.
- Solves the “dying ReLU” problem, where neurons get stuck with zero outputs.
- Range: (-\infty, \infty).
- Preferred in some cases for better gradient flow.
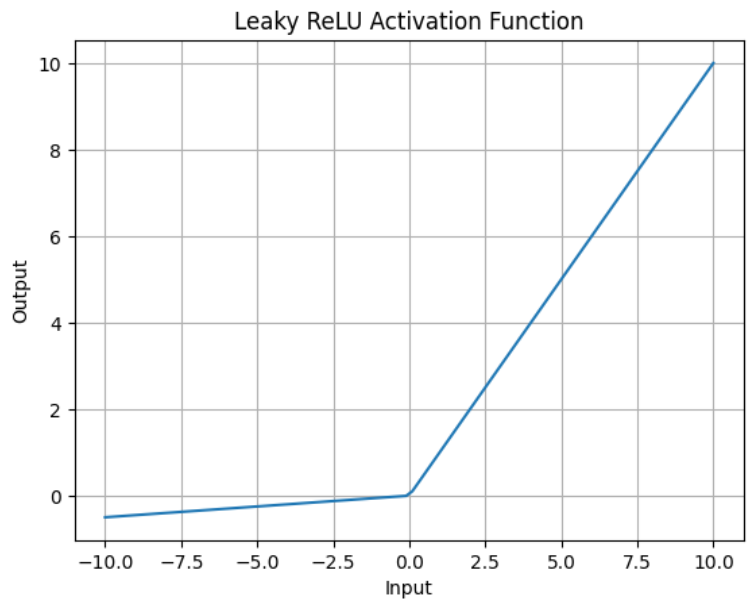 Leaky ReLU Activation Function
Leaky ReLU Activation Function3. Exponential Linear Units
1. Softmax Function
Softmax function is designed to handle multi-class classification problems. It transforms raw output scores from a neural network into probabilities. It works by squashing the output values of each class into the range of 0 to 1 while ensuring that the sum of all probabilities equals 1.
- Softmax is a non-linear activation function.
- The Softmax function ensures that each class is assigned a probability, helping to identify which class the input belongs to.
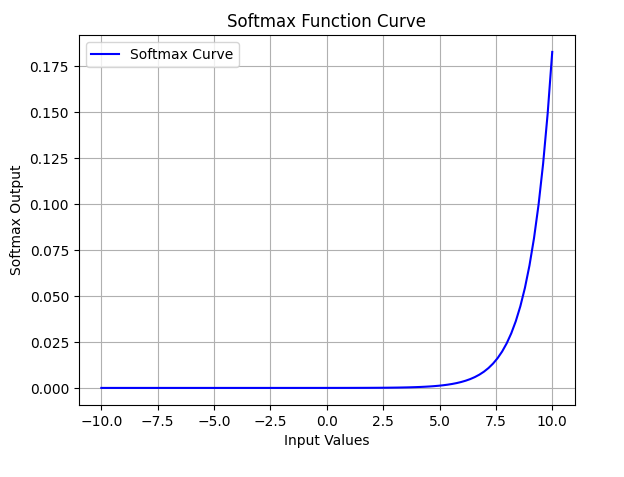 Softmax Activation Function
Softmax Activation Function2. SoftPlus Function
Softplus function is defined mathematically as: A(x) = \log(1 + e^x).
This equation ensures that the output is always positive and differentiable at all points which is an advantage over the traditional ReLU function.
- Nature: The Softplus function is non-linear.
- Range: The function outputs values in the range (0, \infty), similar to ReLU, but without the hard zero threshold that ReLU has.
- Smoothness: Softplus is a smooth, continuous function, meaning it avoids the sharp discontinuities of ReLU which can sometimes lead to problems during optimization.
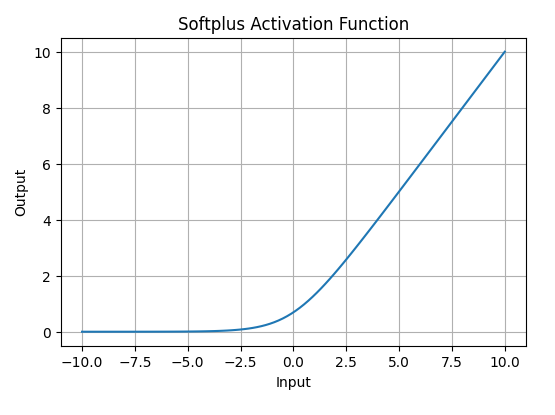 Softplus Activation Function
Softplus Activation FunctionThe choice of activation function has a direct impact on the performance of a neural network in several ways:
- Convergence Speed: Functions like ReLU allow faster training by avoiding the vanishing gradient problem while Sigmoid and Tanh can slow down convergence in deep networks.
- Gradient Flow: Activation functions like ReLU ensure better gradient flow, helping deeper layers learn effectively. In contrast Sigmoid can lead to small gradients, hindering learning in deep layers.
- Model Complexity: Activation functions like Softmax allow the model to handle complex multi-class problems, whereas simpler functions like ReLU or Leaky ReLU are used for basic layers.
Explore
Machine Learning Basics
Python for Machine Learning
Feature Engineering
Supervised Learning
Unsupervised Learning
Model Evaluation and Tuning
Advanced Techniques
Machine Learning Practice
My Profile