Reverse Delete Algorithm for Minimum Spanning Tree
Last Updated : 04 Aug, 2023
Reverse Delete algorithm is closely related to Kruskal's algorithm. In Kruskal's algorithm what we do is : Sort edges by increasing order of their weights. After sorting, we one by one pick edges in increasing order. We include current picked edge if by including this in spanning tree not form any cycle until there are V-1 edges in spanning tree, where V = number of vertices.
In Reverse Delete algorithm, we sort all edges in decreasing order of their weights. After sorting, we one by one pick edges in decreasing order. We include current picked edge if excluding current edge causes disconnection in current graph. The main idea is delete edge if its deletion does not lead to disconnection of graph.
The Algorithm :
- Sort all edges of graph in non-increasing order of edge weights.
- Initialize MST as original graph and remove extra edges using step 3.
- Pick highest weight edge from remaining edges and check if deleting the edge disconnects the graph or not.
If disconnects, then we don't delete the edge.
Else we delete the edge and continue.
Illustration:
Let us understand with the following example:
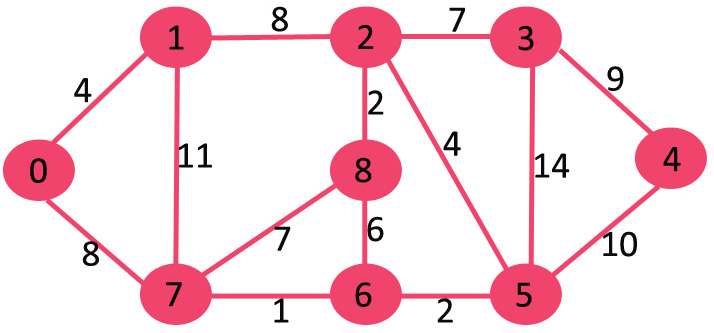
If we delete highest weight edge of weight 14, graph doesn't become disconnected, so we remove it.

Next we delete 11 as deleting it doesn't disconnect the graph.

Next we delete 10 as deleting it doesn't disconnect the graph.

Next is 9. We cannot delete 9 as deleting it causes disconnection.

We continue this way and following edges remain in final MST.
Edges in MST
(3, 4)
(0, 7)
(2, 3)
(2, 5)
(0, 1)
(5, 6)
(2, 8)
(6, 7)
Note : In case of same weight edges, we can pick any edge of the same weight edges.
Implementation:
C++ // C++ program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm #include<bits/stdc++.h> using namespace std; // Creating shortcut for an integer pair typedef pair<int, int> iPair; // Graph class represents a directed graph // using adjacency list representation class Graph { int V; // No. of vertices list<int> *adj; vector< pair<int, iPair> > edges; void DFS(int v, bool visited[]); public: Graph(int V); // Constructor // function to add an edge to graph void addEdge(int u, int v, int w); // Returns true if graph is connected bool isConnected(); void reverseDeleteMST(); }; Graph::Graph(int V) { this->V = V; adj = new list<int>[V]; } void Graph::addEdge(int u, int v, int w) { adj[u].push_back(v); // Add w to v’s list. adj[v].push_back(u); // Add w to v’s list. edges.push_back({w, {u, v}}); } void Graph::DFS(int v, bool visited[]) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex list<int>::iterator i; for (i = adj[v].begin(); i != adj[v].end(); ++i) if (!visited[*i]) DFS(*i, visited); } // Returns true if given graph is connected, else false bool Graph::isConnected() { bool visited[V]; memset(visited, false, sizeof(visited)); // Find all reachable vertices from first vertex DFS(0, visited); // If set of reachable vertices includes all, // return true. for (int i=1; i<V; i++) if (visited[i] == false) return false; return true; } // This function assumes that edge (u, v) // exists in graph or not, void Graph::reverseDeleteMST() { // Sort edges in increasing order on basis of cost sort(edges.begin(), edges.end()); int mst_wt = 0; // Initialize weight of MST cout << "Edges in MST\n"; // Iterate through all sorted edges in // decreasing order of weights for (int i=edges.size()-1; i>=0; i--) { int u = edges[i].second.first; int v = edges[i].second.second; // Remove edge from undirected graph adj[u].remove(v); adj[v].remove(u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (isConnected() == false) { adj[u].push_back(v); adj[v].push_back(u); // This edge is part of MST cout << "(" << u << ", " << v << ") \n"; mst_wt += edges[i].first; } } cout << "Total weight of MST is " << mst_wt; } // Driver code int main() { // create the graph given in above figure int V = 9; Graph g(V); // making above shown graph g.addEdge(0, 1, 4); g.addEdge(0, 7, 8); g.addEdge(1, 2, 8); g.addEdge(1, 7, 11); g.addEdge(2, 3, 7); g.addEdge(2, 8, 2); g.addEdge(2, 5, 4); g.addEdge(3, 4, 9); g.addEdge(3, 5, 14); g.addEdge(4, 5, 10); g.addEdge(5, 6, 2); g.addEdge(6, 7, 1); g.addEdge(6, 8, 6); g.addEdge(7, 8, 7); g.reverseDeleteMST(); return 0; } // Java program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm import java.util.*; // class to represent an edge class Edge implements Comparable<Edge> { int u, v, w; Edge(int u, int v, int w) { this.u = u; this.w = w; this.v = v; } public int compareTo(Edge other) { return (this.w - other.w); } } // Class to represent a graph using adjacency list // representation public class GFG { private int V; // No. of vertices private List<Integer>[] adj; private List<Edge> edges; @SuppressWarnings({ "unchecked", "deprecated" }) public GFG(int v) // Constructor { V = v; adj = new ArrayList[v]; for (int i = 0; i < v; i++) adj[i] = new ArrayList<Integer>(); edges = new ArrayList<Edge>(); } // function to Add an edge public void AddEdge(int u, int v, int w) { adj[u].add(v); // Add w to v’s list. adj[v].add(u); // Add w to v’s list. edges.add(new Edge(u, v, w)); } // function to perform dfs private void DFS(int v, boolean[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex for (int i : adj[v]) { if (!visited[i]) DFS(i, visited); } } // Returns true if given graph is connected, else false private boolean IsConnected() { boolean[] visited = new boolean[V]; // Find all reachable vertices from first vertex DFS(0, visited); // If set of reachable vertices includes all, // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u, v) // exists in graph or not, public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost Collections.sort(edges); int mst_wt = 0; // Initialize weight of MST System.out.println("Edges in MST"); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.size() - 1; i >= 0; i--) { int u = edges.get(i).u; int v = edges.get(i).v; // Remove edge from undirected graph adj[u].remove(adj[u].indexOf(v)); adj[v].remove(adj[v].indexOf(u)); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].add(v); adj[v].add(u); // This edge is part of MST System.out.println("(" + u + ", " + v + ")"); mst_wt += edges.get(i).w; } } System.out.println("Total weight of MST is " + mst_wt); } // Driver code public static void main(String[] args) { // create the graph given in above figure int V = 9; GFG g = new GFG(V); // making above shown graph g.AddEdge(0, 1, 4); g.AddEdge(0, 7, 8); g.AddEdge(1, 2, 8); g.AddEdge(1, 7, 11); g.AddEdge(2, 3, 7); g.AddEdge(2, 8, 2); g.AddEdge(2, 5, 4); g.AddEdge(3, 4, 9); g.AddEdge(3, 5, 14); g.AddEdge(4, 5, 10); g.AddEdge(5, 6, 2); g.AddEdge(6, 7, 1); g.AddEdge(6, 8, 6); g.AddEdge(7, 8, 7); g.ReverseDeleteMST(); } } // This code is contributed by Prithi_Dey # Python3 program to find Minimum Spanning Tree # of a graph using Reverse Delete Algorithm # Graph class represents a directed graph # using adjacency list representation class Graph: def __init__(self, v): # No. of vertices self.v = v self.adj = [0] * v self.edges = [] for i in range(v): self.adj[i] = [] # function to add an edge to graph def addEdge(self, u: int, v: int, w: int): self.adj[u].append(v) # Add w to v’s list. self.adj[v].append(u) # Add w to v’s list. self.edges.append((w, (u, v))) def dfs(self, v: int, visited: list): # Mark the current node as visited and print it visited[v] = True # Recur for all the vertices adjacent to # this vertex for i in self.adj[v]: if not visited[i]: self.dfs(i, visited) # Returns true if graph is connected # Returns true if given graph is connected, else false def connected(self): visited = [False] * self.v # Find all reachable vertices from first vertex self.dfs(0, visited) # If set of reachable vertices includes all, # return true. for i in range(1, self.v): if not visited[i]: return False return True # This function assumes that edge (u, v) # exists in graph or not, def reverseDeleteMST(self): # Sort edges in increasing order on basis of cost self.edges.sort(key = lambda a: a[0]) mst_wt = 0 # Initialize weight of MST print("Edges in MST") # Iterate through all sorted edges in # decreasing order of weights for i in range(len(self.edges) - 1, -1, -1): u = self.edges[i][1][0] v = self.edges[i][1][1] # Remove edge from undirected graph self.adj[u].remove(v) self.adj[v].remove(u) # Adding the edge back if removing it # causes disconnection. In this case this # edge becomes part of MST. if self.connected() == False: self.adj[u].append(v) self.adj[v].append(u) # This edge is part of MST print("( %d, %d )" % (u, v)) mst_wt += self.edges[i][0] print("Total weight of MST is", mst_wt) # Driver Code if __name__ == "__main__": # create the graph given in above figure V = 9 g = Graph(V) # making above shown graph g.addEdge(0, 1, 4) g.addEdge(0, 7, 8) g.addEdge(1, 2, 8) g.addEdge(1, 7, 11) g.addEdge(2, 3, 7) g.addEdge(2, 8, 2) g.addEdge(2, 5, 4) g.addEdge(3, 4, 9) g.addEdge(3, 5, 14) g.addEdge(4, 5, 10) g.addEdge(5, 6, 2) g.addEdge(6, 7, 1) g.addEdge(6, 8, 6) g.addEdge(7, 8, 7) g.reverseDeleteMST() # This code is contributed by # sanjeev2552 // C# program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm using System; using System.Collections.Generic; // class to represent an edge public class Edge : IComparable<Edge> { public int u, v, w; public Edge(int u, int v, int w) { this.u = u; this.v = v; this.w = w; } public int CompareTo(Edge other) { return this.w.CompareTo(other.w); } } // Graph class represents a directed graph // using adjacency list representation public class Graph { private int V; // No. of vertices private List<int>[] adj; private List<Edge> edges; public Graph(int v) // Constructor { V = v; adj = new List<int>[ v ]; for (int i = 0; i < v; i++) adj[i] = new List<int>(); edges = new List<Edge>(); } // function to Add an edge public void AddEdge(int u, int v, int w) { adj[u].Add(v); // Add w to v’s list. adj[v].Add(u); // Add w to v’s list. edges.Add(new Edge(u, v, w)); } // function to perform dfs private void DFS(int v, bool[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex foreach(int i in adj[v]) { if (!visited[i]) DFS(i, visited); } } // Returns true if given graph is connected, else false private bool IsConnected() { bool[] visited = new bool[V]; // Find all reachable vertices from first vertex DFS(0, visited); // If set of reachable vertices includes all, // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u, v) // exists in graph or not, public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost edges.Sort(); int mst_wt = 0; // Initialize weight of MST Console.WriteLine("Edges in MST"); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.Count - 1; i >= 0; i--) { int u = edges[i].u; int v = edges[i].v; // Remove edge from undirected graph adj[u].Remove(v); adj[v].Remove(u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].Add(v); adj[v].Add(u); // This edge is part of MST Console.WriteLine("({0}, {1})", u, v); mst_wt += edges[i].w; } } Console.WriteLine("Total weight of MST is {0}", mst_wt); } } class GFG { // Driver code static void Main(string[] args) { // create the graph given in above figure int V = 9; Graph g = new Graph(V); // making above shown graph g.AddEdge(0, 1, 4); g.AddEdge(0, 7, 8); g.AddEdge(1, 2, 8); g.AddEdge(1, 7, 11); g.AddEdge(2, 3, 7); g.AddEdge(2, 8, 2); g.AddEdge(2, 5, 4); g.AddEdge(3, 4, 9); g.AddEdge(3, 5, 14); g.AddEdge(4, 5, 10); g.AddEdge(5, 6, 2); g.AddEdge(6, 7, 1); g.AddEdge(6, 8, 6); g.AddEdge(7, 8, 7); g.ReverseDeleteMST(); } } // This code is contributed by cavi4762 // Javascript program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm // Graph class represents a directed graph // using adjacency list representation class Graph { // Constructor constructor(V) { this.V = V; this.adj = []; this.edges = []; for (let i = 0; i < V; i++) { this.adj[i] = []; } } // function to add an edge to graph addEdge(u, v, w) { this.adj[u].push(v);// Add w to v’s list. this.adj[v].push(u);// Add w to v’s list. this.edges.push([w, [u, v]]); } DFS(v, visited) { // Mark the current node as visited and print it visited[v] = true; for (const i of this.adj[v]) { if (!visited[i]) { this.DFS(i, visited); } } } // Returns true if given graph is connected, else false isConnected() { const visited = []; for (let i = 0; i < this.V; i++) { visited[i] = false; } // Find all reachable vertices from first vertex this.DFS(0, visited); // If set of reachable vertices includes all, // return true. for (let i = 1; i < this.V; i++) { if (!visited[i]) { return false; } } return true; } // This function assumes that edge (u, v) // exists in graph or not, reverseDeleteMST() { // Sort edges in increasing order on basis of cost this.edges.sort((a, b) => a[0] - b[0]); let mstWt = 0;// Initialize weight of MST console.log("Edges in MST"); // Iterate through all sorted edges in // decreasing order of weights for (let i = this.edges.length - 1; i >= 0; i--) { const [u, v] = this.edges[i][1]; // Remove edge from undirected graph this.adj[u] = this.adj[u].filter(x => x !== v); this.adj[v] = this.adj[v].filter(x => x !== u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (!this.isConnected()) { this.adj[u].push(v); this.adj[v].push(u); // This edge is part of MST console.log(`(${u}, ${v})`); mstWt += this.edges[i][0]; } } console.log(`Total weight of MST is ${mstWt}`); } } // Driver code function main() { // create the graph given in above figure var V = 9; var g = new Graph(V); // making above shown graph g.addEdge(0, 1, 4); g.addEdge(0, 7, 8); g.addEdge(1, 2, 8); g.addEdge(1, 7, 11); g.addEdge(2, 3, 7); g.addEdge(2, 8, 2); g.addEdge(2, 5, 4); g.addEdge(3, 4, 9); g.addEdge(3, 5, 14); g.addEdge(4, 5, 10); g.addEdge(5, 6, 2); g.addEdge(6, 7, 1); g.addEdge(6, 8, 6); g.addEdge(7, 8, 7); g.reverseDeleteMST(); } main(); OutputEdges in MST (3, 4) (0, 7) (2, 3) (2, 5) (0, 1) (5, 6) (2, 8) (6, 7) Total weight of MST is 37
Time complexity: O((E*(V+E)) + E log E) where E is the number of edges.
Space complexity: O(V+E) where V is the number of vertices and E is the number of edges. We are using adjacency list to store the graph, so we need space proportional to O(V+E).
Notes :
- The above implementation is a simple/naive implementation of Reverse Delete algorithm and can be optimized to O(E log V (log log V)3) [Source : Wiki]. But this optimized time complexity is still less than Prim and Kruskal Algorithms for MST.
- The above implementation modifies the original graph. We can create a copy of the graph if original graph must be retained.
Explore
DSA Fundamentals
Data Structures
Algorithms
Advanced
Interview Preparation
Practice Problem