Number of Unique BST with N Keys

Last Updated : 11 Jul, 2025

Given an integer n, the task is to find the total number of unique BSTs that can be made using values from 1 to n.

Examples:

Input: n = 3
Output: 5
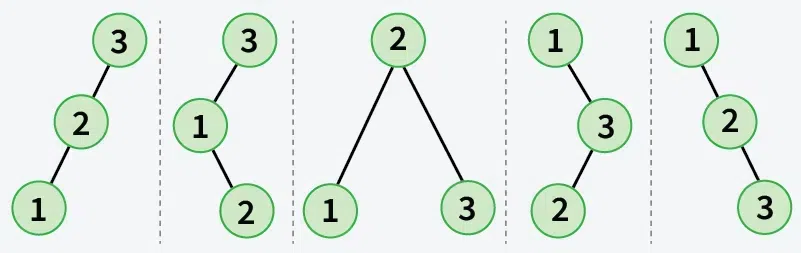
Explanation: For n = 3, preorder traversal of Unique BSTs are:
1 2 3
1 3 2
2 1 3
3 1 2
3 2 1

Input: n = 2
Output: 2
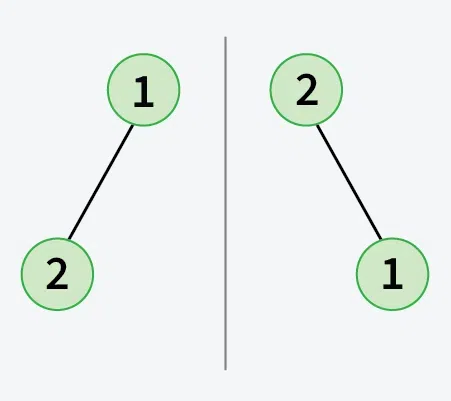
Explanation: For n = 2, preorder traversal of Unique BSTs are:
1 2
2 1

Approach:

A binary search tree (BST) maintains the property that elements are arranged based on their relative order. Let’s define C(n) as the number of unique BSTs that can be constructed with n nodes.
When considering all possible BSTs, each of the n nodes can serve as the root. For any selected root, the remaining n-1 nodes must be divided into two groups:
Nodes with keys smaller than the root’s key
Nodes with keys larger than the root’s key.
Assume we choose the node with the i-th key as the root. In this scenario, there will be i-1 nodes that are smaller and n-i nodes that are larger than the chosen root. This leads to dividing the problem of counting the total BSTs with the i-th key as the root into two subproblems:
Calculating the number of unique BSTs for the left subtree containing i-1 nodes, represented as C(i-1).
Calculating the number of unique BSTs for the right subtree containing n-i nodes, represented as C(n-i).
Since the left and right subtrees are constructed independently, we multiply these counts to get the total number of BSTs for the current configuration: C(i-1) * C(n-i).
To find the total number of BSTs with n nodes, we sum this product across all possible roots (i.e., from i = 1 to n). Therefore,
C(n) = Σ(i = 1 to n) C(i-1) * C(n-i).
This formula corresponds to the recurrence relation for the nth Catalan number. So this is how it is a classic application of Catalan number. We just need to find nth catalan number. First few catalan numbers are 1 1 2 5 14 42 132 429 1430 4862, … (considered from 0th number).
Formula of catalan number is (1 / n+1) * ( ^2*nCn). Please refer to Applications of Catalan Numbers.

C++

// C++ code of finding Number of Unique // BST with N Keys  #include <iostream> using namespace std; // Function to calculate the binomial // coefficient C(n, k) int binomialCoeff(int n, int k) {    // C(n, k) is the same as C(n, n-k)  if (k > n - k) {  k = n - k;  }  int res = 1;    // Calculate the value of n! / (k! * (n-k)!)  for (int i = 0; i < k; ++i) {  res *= (n - i);  res /= (i + 1);  }  return res; } // Function to find the nth Catalan number int numTrees(int n) {    // Calculate C(2n, n)  int c = binomialCoeff(2 * n, n);    // Return the nth Catalan number  return c / (n + 1); } int main() {    int n = 5;  cout << numTrees(n) << endl;  return 0; }

Java

// Java program to find the number of unique // BSTs with N keys class GfG {    // Function to calculate the binomial  // coefficient C(n, k)  static int binomialCoeff(int n, int k) {    // C(n, k) is the same as C(n, n-k)  if (k > n - k) {  k = n - k;  }  int res = 1;    // Calculate the value of n! / (k! * (n-k)!)  for (int i = 0; i < k; ++i) {  res *= (n - i);  res /= (i + 1);  }  return res;  }  // Function to find the nth Catalan number  static int numTrees(int n) {    // Calculate C(2n, n)  int c = binomialCoeff(2 * n, n);  // Return the nth Catalan number  return c / (n + 1);  }  public static void main(String[] args) {  int n = 5;  System.out.println(numTrees(n));  } }

Python

# Python program to find the number of unique  # BSTs with N keys # Function to calculate the binomial coefficient C(n, k) def binomial_coeff(n, k): # C(n, k) is the same as C(n, n-k) if k > n - k: k = n - k res = 1 # Calculate the value of n! / (k! * (n-k)!) for i in range(k): res *= (n - i) res //= (i + 1) return res # Function to find the nth Catalan number def numTrees(n): # Calculate C(2n, n) c = binomial_coeff(2 * n, n) # Return the nth Catalan number return c // (n + 1) n = 5 print(numTrees(n))

// C# program to find the number of unique // BSTs with N keys using System; class GfG {    // Function to calculate the binomial  // coefficient C(n, k)  static int BinomialCoeff(int n, int k) {    // C(n, k) is the same as C(n, n-k)  if (k > n - k) {  k = n - k;  }  int res = 1;    // Calculate the value of n! / (k! * (n-k)!)  for (int i = 0; i < k; ++i) {  res *= (n - i);  res /= (i + 1);  }  return res;  }  // Function to find the nth Catalan  // number  static int numTrees(int n) {    // Calculate C(2n, n)  int c = BinomialCoeff(2 * n, n);  // Return the nth Catalan number  return c / (n + 1);  }  static void Main() {  int n = 5;  Console.WriteLine(numTrees(n));  } }

JavaScript

// JavaScript program to find the number of unique BSTs with // n keys // Function to calculate the binomial coefficient C(n, k) function binomialCoeff(n, k) {  // C(n, k) is the same as C(n, n-k)  if (k > n - k) {  k = n - k;  }  let res = 1;    // Calculate the value of n! / (k! * (n-k)!)  for (let i = 0; i < k; i++) {  res *= (n - i);  res /= (i + 1);  }  return res; } // Function to find the nth Catalan number function numTrees(n) {  // Calculate C(2n, n)  let c = binomialCoeff(2 * n, n);  // Return the nth Catalan number  return c / (n + 1); } const n = 5; console.log(numTrees(n));