Maximum sum rectangle in a 2D matrix

Last Updated : 28 Jul, 2025

Given a 2D matrix mat[][] of integers, find the submatrix (i.e., a rectangular section of the matrix) that has the maximum possible sum among all possible submatrices.

Example:

Input: mat[][] = [[1, 2, -1, -4, -20],
[-8, -3, 4, 2, 1],
[3, 8, 10, 1, 3],
[-4, -1, 1, 7, -6]]
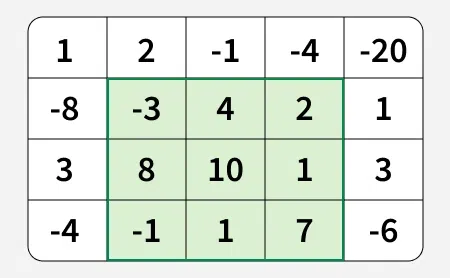
Output: 29
Explanation: The matrix is as follows and the green rectangle denotes the maximum sum rectangle which is equal to 29.

This problem is mainly an extension of the Maximum Subarray Sum.

Table of Content

[Naive approach] Iterating Over All Possible Submatrices

We explore all possible rectangles in the given 2D array, by using four variables: two to define the left and right boundaries and two more to define the top and bottom boundaries and calculate their sums, and keep track of the maximum sum found.

C++

#include <iostream> #include <vector> #include <climits> using namespace std; int maxRectSum(vector<vector<int>> &mat) {    int n = mat.size();  int m = mat[0].size();  int maxSum = INT_MIN;  for (int up = 0; up < n; up++) {  for (int left = 0; left < m; left++) {  for (int down = up; down < n; down++) {  for (int right = left; right < m; right++) {    // Find the sum of submatrix(up, right, down, left)  int sum = 0;  for (int i = up; i <= down; i++) {  for (int j = left; j <= right; j++) {  sum += mat[i][j];  }  }  // Update maxSum if sum > maxSum.  if (sum > maxSum) {  maxSum = sum;  }  }  }  }  }  return maxSum; } int main() {  vector<vector<int>> mat = {{1, 2, -1, -4, -20},   {-8, -3, 4, 2, 1},   {3, 8, 10, 1, 3},   {-4, -1, 1, 7, -6}};    cout << maxRectSum(mat) << endl;  return 0; }

Java

class GfG {  static int maxRectSum(int[][] mat) {  int n = mat.length;  int m = mat[0].length;  int maxSum = Integer.MIN_VALUE;  for (int up = 0; up < n; up++) {  for (int left = 0; left < m; left++) {  for (int down = up; down < n; down++) {  for (int right = left; right < m; right++) {    // Find the sum of  // submatrix(up, right, down, left)  int sum = 0;  for (int i = up;  i <= down; i++) {  for (int j = left;  j <= right; j++) {  sum += mat[i][j];  }  }  // Update maxSum if sum > maxSum.  if (sum > maxSum) {  maxSum = sum;  }  }  }  }  }  return maxSum;  }  public static void main(String[] args) {  int[][] mat = { { 1, 2, -1, -4, -20 },  { -8, -3, 4, 2, 1 },  { 3, 8, 10, 1, 3 },  { -4, -1, 1, 7, -6 } };  System.out.println(maxRectSum(mat));  } }

Python

def maxRectSum(mat): n = len(mat) m = len(mat[0]) maxSum = float('-inf') for up in range(n): for left in range(m): for down in range(up, n): for right in range(left, m): # Calculate the sum of submatrix  # (up, left, down, right) subMatrixSum = 0 for i in range(up, down + 1): for j in range(left, right + 1): subMatrixSum += mat[i][j] # Update maxSum if a larger sum is found maxSum = max(maxSum, subMatrixSum) return maxSum if __name__ == "__main__": mat = [ [1, 2, -1, -4, -20], [-8, -3, 4, 2, 1], [3, 8, 10, 1, 3], [-4, -1, 1, 7, -6] ] print(maxRectSum(mat))

using System; class GfG {  static int maxRectSum(int[][] mat) {  int n = mat.Length;  int m = mat[0].Length;  int maxSum = int.MinValue;  for (int up = 0; up < n; up++) {  for (int left = 0; left < m; left++) {  for (int down = up; down < n; down++) {  for (int right = left; right < m; right++) {    // Calculate the sum of submatrix   // (up, left, down, right)  int subMatrixSum = 0;  for (int i = up; i <= down; i++) {  for (int j = left; j <= right; j++) {  subMatrixSum += mat[i][j];  }  }  // Update maxSum if a larger sum is found  maxSum = Math.Max(maxSum, subMatrixSum);  }  }  }  }  return maxSum;  }  static void Main(string[] args) {  int[][] mat = {   new int[] { 1, 2, -1, -4, -20 },  new int[] { -8, -3, 4, 2, 1 },  new int[] { 3, 8, 10, 1, 3 },  new int[] { -4, -1, 1, 7, -6 }   };  Console.WriteLine(maxRectSum(mat));   } }

JavaScript

function maxRectSum(mat) {  const n = mat.length;  const m = mat[0].length;  let maxSum = -Infinity;  for (let up = 0; up < n; up++) {  for (let left = 0; left < m; left++) {  for (let down = up; down < n; down++) {  for (let right = left; right < m; right++) {    // Calculate the sum of submatrix   // (up, left, down, right)  let subMatrixSum = 0;  for (let i = up; i <= down; i++) {  for (let j = left; j <= right; j++) {  subMatrixSum += mat[i][j];  }  }  // Update maxSum if a larger sum is  // found  maxSum = Math.max(maxSum, subMatrixSum);  }  }  }  }  return maxSum; } // Driver Code const mat = [  [ 1, 2, -1, -4, -20 ],   [ -8, -3, 4, 2, 1 ],  [ 3, 8, 10, 1, 3 ],   [ -4, -1, 1, 7, -6 ] ]; console.log(maxRectSum(mat));

Time Complexity: O((n*m)³), as we iterate over all the boundaries of the rectangle in O((n*m)²) time. For each rectangle, we find its sum in O(n*m) time.
Auxiliary Space: O(1)

[Better Approach] Using Prefix Sum

In this approach, we used prefix sum matrix to efficiently compute the sum of any submatrix. We first precompute the prefix sum such that pref[i][j] stores the sum of all elements in the submatrix from the top-left corner (0, 0) to the cell (i, j). This preprocessing allows us to calculate the sum of any arbitrary submatrix in constant time using the inclusion-exclusion principle, thereby eliminating redundant computations and significantly improving performance.

Step by Step Approach:

Initialize a 2D prefix sum matrix pref[][] of the same size as the input matrix.
Precompute the prefix sum for each cell : pref[i][j] = matrix[i][j] + pref[i−1][j] + pref[i][j−1] − pref[i−1][j−1] (Handle edges separately to avoid index out-of-bound errors.)
Iterate over all possible top-left corners (up, left) and bottom-right corners (down, right) to define submatrices.
For each such submatrix, compute the sum using the prefix sum matrix in constant time: sum = pref[down][right] − pref[up - 1][right] − pref[down][left−1] + pref[up-1][left - 1]
Track the maximum sum obtained across all submatrices.

C++

#include <iostream> #include <vector> #include <climits> using namespace std; int findSum(int up, int left, int down, int right,   vector<vector<int>> &pref) {    // Start with the sum of the entire submatrix (0, 0) to (down, right)  int sum = pref[down][right];   // Subtract the area to the left of the submatrix, if it exists  if (left - 1 >= 0) {  sum -= pref[down][left - 1];  }  // Subtract the area above the submatrix, if it exists  if (up - 1 >= 0) {  sum -= pref[up - 1][right];  }  // Add back the overlapping area that was subtracted twice  if (up - 1 >= 0 && left - 1 >= 0) {  sum += pref[up - 1][left - 1];  }  return sum; } // function to find the maximum sum rectangle in a 2D matrix int maxRectSum(vector<vector<int>> &mat) {  int n = mat.size();  int m = mat[0].size();  // Initialize the prefix sum matrix  vector<vector<int>> pref(n, vector<int>(m, 0));  // Row-wise sum  for (int i = 0; i < n; i++) {  for (int j = 0; j < m; j++) {  pref[i][j] = mat[i][j];  if (j - 1 >= 0) {  pref[i][j] += pref[i][j - 1];  }  }  }  // Column-wise sum  for (int j = 0; j < m; j++) {  for (int i = 0; i < n; i++) {  if (i - 1 >= 0) {  pref[i][j] += pref[i - 1][j];  }  }  }  int maxSum = INT_MIN;  for (int up = 0; up < n; up++) {  for (int left = 0; left < m; left++) {  for (int down = up; down < n; down++) {  for (int right = left; right < m; right++) {    // Find the sum of submatrix(up, right, down, left)  int sum = findSum(up, left, down, right, pref);  // Update maxSum if sum > maxSum.  if (sum > maxSum) {  maxSum = sum;  }  }  }  }  }  return maxSum; } int main() {  vector<vector<int>> mat = {{1, 2, -1, -4, -20},   {-8, -3, 4, 2, 1},   {3, 8, 10, 1, 3},   {-4, -1, 1, 7, -6}};  cout << maxRectSum(mat) << endl; }

Java

import java.util.*; class GfG {    static int findSum(int up, int left, int down, int right,  int[][] pref) {  // Start with the sum of the entire submatrix   // (0, 0) to (down, right)  int sum = pref[down][right];    // Subtract the area to the left of the submatrix, if it exists  if (left - 1 >= 0) {  sum -= pref[down][left - 1];  }    // Subtract the area above the submatrix, if it exists  if (up - 1 >= 0) {  sum -= pref[up - 1][right];  }    // Add back the overlapping area that was subtracted twice  if (up - 1 >= 0 && left - 1 >= 0) {  sum += pref[up - 1][left - 1];  }    return sum;  }  // function to find the maximum sum rectangle in a 2D matrix  public static int maxRectSum(int[][] mat) {  int n = mat.length;  int m = mat[0].length;  // Initialize the prefix sum matrix  int[][] pref = new int[n][m];  // Row-wise sum  for (int i = 0; i < n; i++) {  for (int j = 0; j < m; j++) {  pref[i][j] = mat[i][j];  if (j - 1 >= 0) {  pref[i][j] += pref[i][j - 1];  }  }  }  // Column-wise sum  for (int j = 0; j < m; j++) {  for (int i = 0; i < n; i++) {  if (i - 1 >= 0) {  pref[i][j] += pref[i - 1][j];  }  }  }  // Find the maximum sum rectangle  int maxSum = Integer.MIN_VALUE;  for (int up = 0; up < n; up++) {  for (int left = 0; left < m; left++) {  for (int down = up; down < n; down++) {  for (int right = left; right < m;  right++) {  // Find the sum of the submatrix  // (up, left) to  // (down, right)  int sum = findSum( up, left, down,   right, pref);  // Update maxSum if sum > maxSum  if (sum > maxSum) {  maxSum = sum;  }  }  }  }  }  return maxSum;  }  public static void main(String[] args) {  int[][] mat = { { 1, 2, -1, -4, -20 },  { -8, -3, 4, 2, 1 },  { 3, 8, 10, 1, 3 },  { -4, -1, 1, 7, -6 } };  System.out.println(maxRectSum(mat));  } }

Python

def findSum(up, left, down, right, pref): # Start with the sum of the entire submatrix (0, 0) to (down, right) totalSum = pref[down][right] # Subtract the area to the left of the submatrix, if it exists if left - 1 >= 0: totalSum -= pref[down][left - 1] # Subtract the area above the submatrix, if it exists if up - 1 >= 0: totalSum -= pref[up - 1][right] # Add back the overlapping area that was subtracted twice if up - 1 >= 0 and left - 1 >= 0: totalSum += pref[up - 1][left - 1] return totalSum # Function to find the maximum sum rectangle in a 2D matrix def maxRectSum(mat): n = len(mat) m = len(mat[0]) # Initialize the prefix sum matrix pref = [[0] * m for _ in range(n)] # Row-wise sum for i in range(n): for j in range(m): pref[i][j] = mat[i][j] if j - 1 >= 0: pref[i][j] += pref[i][j - 1] # Column-wise sum for j in range(m): for i in range(n): if i - 1 >= 0: pref[i][j] += pref[i - 1][j] # Find the maximum sum rectangle maxSum = float('-inf') for up in range(n): for left in range(m): for down in range(up, n): for right in range(left, m): totalSum = findSum(up, left, down, right, pref) maxSum = max(maxSum, totalSum) return maxSum if __name__ == "__main__": mat = [ [1, 2, -1, -4, -20], [-8, -3, 4, 2, 1], [3, 8, 10, 1, 3], [-4, -1, 1, 7, -6] ] print(maxRectSum(mat))

using System; class GfG {  static int findSum(int up, int left, int down, int right, int[,] pref) {  // Start with the sum of the entire submatrix from (0,0) to (down,right)  int sum = pref[down, right];  // Subtract the area to the left of the submatrix, if it exists  if (left - 1 >= 0)  sum -= pref[down, left - 1];  // Subtract the area above the submatrix, if it exists  if (up - 1 >= 0)  sum -= pref[up - 1, right];  // Add back the overlapping area that was subtracted twice  if (up - 1 >= 0 && left - 1 >= 0)  sum += pref[up - 1, left - 1];  return sum;  }  static int maxRectSum(int[,] mat) {  int n = mat.GetLength(0);  int m = mat.GetLength(1);  // Initialize the prefix sum matrix  int[,] pref = new int[n, m];  // Compute row-wise prefix sum  for (int i = 0; i < n; i++) {  for (int j = 0; j < m; j++) {  pref[i, j] = mat[i, j];  if (j - 1 >= 0)  pref[i, j] += pref[i, j - 1];  }  }  // Compute column-wise prefix sum  for (int j = 0; j < m; j++) {  for (int i = 0; i < n; i++) {  if (i - 1 >= 0)  pref[i, j] += pref[i - 1, j];  }  }  int maxSum = int.MinValue;  // Check all possible submatrices  for (int up = 0; up < n; up++) {  for (int left = 0; left < m; left++) {  for (int down = up; down < n; down++) {  for (int right = left; right < m; right++) {  int totalSum = findSum(up, left, down, right, pref);  if (totalSum > maxSum)  maxSum = totalSum;  }  }  }  }  return maxSum;  }  static void Main(string[] args) {  int[,] mat = new int[,]  {  { 1, 2, -1, -4, -20 },  { -8, -3, 4, 2, 1 },  { 3, 8, 10, 1, 3 },  { -4, -1, 1, 7, -6 }  };  Console.WriteLine(maxRectSum(mat));   } }

JavaScript

// Function to get the sum of submatrix (r1, c1) to (r2, c2) function findSum(up, left, down, right, pref) {    // Start with the sum of the entire submatrix (0, 0) to (down, right)  let sum = pref[down][right];   // Subtract the area to the left of the submatrix, if it exists  if (left - 1 >= 0) {  sum -= pref[down][left - 1];  }  // Subtract the area above the submatrix, if it exists  if (up - 1 >= 0) {  sum -= pref[up - 1][right];  }  // Add back the overlapping area that was subtracted twice  if (up - 1 >= 0 && left - 1 >= 0) {  sum += pref[up - 1][left - 1];  }  return sum; } // function to find the maximum sum rectangle in a 2D matrix function maxRectSum(mat) {  const n = mat.length;  const m = mat[0].length;  // Create and initialize prefix sum matrix  const pref = Array.from({ length: n }, () => Array(m).fill(0));  // Row-wise prefix sum  for (let i = 0; i < n; i++) {  for (let j = 0; j < m; j++) {  pref[i][j] = mat[i][j];  if (j - 1 >= 0) {  pref[i][j] += pref[i][j - 1];  }  }  }  // Column-wise prefix sum  for (let j = 0; j < m; j++) {  for (let i = 0; i < n; i++) {  if (i - 1 >= 0) {  pref[i][j] += pref[i - 1][j];  }  }  }  let maxSum = -Infinity;  // Try all submatrices  for (let up = 0; up < n; up++) {  for (let left = 0; left < m; left++) {  for (let down = up; down < n; down++) {  for (let right = left; right < m; right++) {  let sum = findSum(up, left, down, right, pref);  if (sum > maxSum) {  maxSum = sum;  }  }  }  }  }  return maxSum; } // Driver code const mat = [  [ 1, 2, -1, -4, -20 ],  [ -8, -3, 4, 2, 1 ],  [ 3, 8, 10, 1, 3 ],  [ -4, -1, 1, 7, -6 ] ]; console.log(maxRectSum(mat)); // Output: 29

Time Complexity: O((n*m)²)
Auxiliary Space: O(n*m), due to the prefix sum matrix.

[Expected Approach] Using Kadane’s Algorithm

Instead of checking every possible submatrix, we fix two column boundaries: left and right. For each pair of columns, we compress the 2D matrix into a 1D array, where each element represents the sum of rows between the current left and right columns. This 1D array (temp[]) represents the column-wise sum for a fixed column window.
Now, we can apply Kadane’s algorithm on this temp[] array to find the maximum subarray sum, which corresponds to a rectangular submatrix with the maximum sum between columns left and right.

C++

#include <iostream> #include <vector> #include <climits> using namespace std; // Kadane's algorithm to find the maximum sum  // subarray in a 1D array int kadane(vector<int>& temp) {  int rows = temp.size();  int currSum = 0;  int maxSum = INT_MIN;  for (int i = 0; i < rows; i++) {  currSum += temp[i];  // Update maxSum if the current sum is greater  if (maxSum < currSum) {  maxSum = currSum;  }  // If the current sum becomes negative, reset it to 0  if (currSum < 0) {  currSum = 0;  }  }  return maxSum; } // Function to find the maximum sum rectangle in a 2D matrix int maxRectSum(vector<vector<int>> &mat) {  int rows = mat.size();  int cols = mat[0].size();  int maxSum = INT_MIN;  // Initialize a temporary array to store row-wise  // sums between left and right boundaries  vector<int> temp(rows);  // Check for all possible left and right boundaries  for (int left = 0; left < cols; left++) {    // Reset the temporary array for each new left boundary  for (int i = 0; i < rows; i++)  temp[i] = 0;  for (int right = left; right < cols; right++) {    // Update the temporary array with the current  // column's values  for (int row = 0; row < rows; row++) {  temp[row] += mat[row][right];  }  // Find the maximum sum of the subarray for the   // current column boundaries  int sum = kadane(temp);  // Update the maximum sum found so far  maxSum = max(maxSum, sum);  }  }  return maxSum; } int main() {  vector<vector<int>> mat = {{1, 2, -1, -4, -20},  {-8, -3, 4, 2, 1},   {3, 8, 10, 1, 3},  {-4, -1, 1, 7, -6}};  int res = maxRectSum(mat);   cout << res << endl;   return 0; }

Java

class GfG {  // Kadane's algorithm to find the maximum sum subarray  // in a 1D array  static int kadane(int[] temp) {  int rows = temp.length;  int currSum = 0;  int maxSum = Integer.MIN_VALUE;  for (int i = 0; i < rows; i++) {  currSum += temp[i];  // Update maxSum if the current sum is greater  if (maxSum < currSum) {  maxSum = currSum;  }  // If the current sum becomes negative, reset it  // to 0  if (currSum < 0) {  currSum = 0;  }  }  return maxSum;  }  // Function to find the maximum sum rectangle in a 2D  // matrix  static int maxRectSum(int[][] mat) {  int rows = mat.length;  int cols = mat[0].length;  int maxSum = Integer.MIN_VALUE;  // Initialize a temporary array to store row-wise  // sums between left and right boundaries  int[] temp = new int[rows];  // Check for all possible left and right boundaries  for (int left = 0; left < cols; left++) {    // Reset the temporary array for each new left  // boundary  for (int i = 0; i < rows; i++) {  temp[i] = 0;  }  for (int right = left; right < cols; right++) {    // Update the temporary array with the  // current column's values  for (int row = 0; row < rows; row++) {  temp[row] += mat[row][right];  }  // Find the maximum sum of the subarray for  // the current column boundaries  int sum = kadane(temp);  // Update the maximum sum found so far  maxSum = Math.max(maxSum, sum);  }  }  return maxSum;  }  public static void main(String[] args) {  int[][] mat = { { 1, 2, -1, -4, -20 },  { -8, -3, 4, 2, 1 },  { 3, 8, 10, 1, 3 },  { -4, -1, 1, 7, -6 } };  int res = maxRectSum(mat);  System.out.println(res);  } }

Python

def kadane(temp): rows = len(temp) currSum = 0 maxSum = float('-inf') for i in range(rows): currSum += temp[i] # Update maxSum if the current sum is greater if maxSum < currSum: maxSum = currSum # If the current sum becomes negative, reset it to 0 if currSum < 0: currSum = 0 return maxSum def maxRectSum(mat): rows = len(mat) cols = len(mat[0]) maxSum = float('-inf') # Initialize a temporary array to store row-wise # sums between left and right boundaries temp = [0] * rows # Check for all possible left and right boundaries for left in range(cols): # Reset the temporary array for each new left # boundary temp = [0] * rows for right in range(left, cols): # Update the temporary array with the current # column's values for row in range(rows): temp[row] += mat[row][right] # Find the maximum sum of the subarray for the # current column boundaries sumValue = kadane(temp) # Update the maximum sum found so far maxSum = max(maxSum, sumValue) return maxSum if __name__ == "__main__": mat = [ [1, 2, -1, -4, -20], [-8, -3, 4, 2, 1], [3, 8, 10, 1, 3], [-4, -1, 1, 7, -6] ] res = maxRectSum(mat) print(res)

using System; class GfG {    // Function to apply Kadane's algorithm to find the  // maximum sum subarray  static int kadane(int[] temp) {  int rows = temp.Length;  int currSum = 0;  int maxSum = int.MinValue;  for (int i = 0; i < rows; i++) {  currSum += temp[i];  // Update maxSum if the current sum is greater  if (maxSum < currSum) {  maxSum = currSum;  }  // If the current sum becomes negative, reset it  // to 0  if (currSum < 0) {  currSum = 0;  }  }  return maxSum;  }  // Function to find the maximum sum of submatrix  static int maxRectSum(int[, ] mat) {  int rows = mat.GetLength(0);  int cols = mat.GetLength(1);  int maxSum = int.MinValue;  // Initialize a temporary array to store row-wise  // sums between left and right boundaries  int[] temp = new int[rows];  // Check for all possible left and right boundaries  for (int left = 0; left < cols; left++) {    // Reset the temporary array for each new left  // boundary  Array.Clear(temp, 0, rows);  for (int right = left; right < cols; right++) {    // Update the temporary array with the  // current column's values  for (int row = 0; row < rows; row++) {  temp[row] += mat[row, right];  }  // Find the maximum sum of the subarray for  // the current column boundaries  int sumValue = kadane(temp);  // Update the maximum sum found so far  maxSum = Math.Max(maxSum, sumValue);  }  }  return maxSum;  }  static void Main() {    int[, ] mat = { { 1, 2, -1, -4, -20 },  { -8, -3, 4, 2, 1 },  { 3, 8, 10, 1, 3 },  { -4, -1, 1, 7, -6 } };  int res = maxRectSum(mat);  Console.WriteLine(res);  } }

JavaScript

// Function to apply Kadane's algorithm to find the maximum // sum subarray function kadane(temp) {  let rows = temp.length;  let currSum = 0;  let maxSum = -Infinity;  for (let i = 0; i < rows; i++) {  currSum += temp[i];  // Update maxSum if the current sum is greater  if (maxSum < currSum) {  maxSum = currSum;  }  // If the current sum becomes negative, reset it to  // 0  if (currSum < 0) {  currSum = 0;  }  }  return maxSum; } // Function to find the maximum sum of submatrix function maxRectSum(mat) {  const rows = mat.length;  const cols = mat[0].length;  let maxSum = -Infinity;  // Initialize a temporary array to store row-wise sums  // between left and right boundaries  let temp = new Array(rows).fill(0);  // Check for all possible left and right boundaries  for (let left = 0; left < cols; left++) {    // Reset the temporary array for each new left  // boundary  temp.fill(0);  for (let right = left; right < cols; right++) {    // Update the temporary array with the current  // column's values  for (let row = 0; row < rows; row++) {  temp[row] += mat[row][right];  }  // Find the maximum sum of the subarray for the  // current column boundaries  let sumValue = kadane(temp, rows);  // Update the maximum sum found so far  maxSum = Math.max(maxSum, sumValue);  }  }  return maxSum; } // Driver Code const mat = [  [ 1, 2, -1, -4, -20 ],   [ -8, -3, 4, 2, 1 ],  [ 3, 8, 10, 1, 3 ],   [ -4, -1, 1, 7, -6 ] ]; const res = maxRectSum(mat); console.log(res);