Insertion in Binary Search Tree (BST)
Last Updated : 08 Dec, 2025
Given the root of a Binary Search Tree, we need to insert a new node with given value in the BST. All the nodes have distinct values in the BST and we may assume that the the new value to be inserted is not present in BST.
Example:
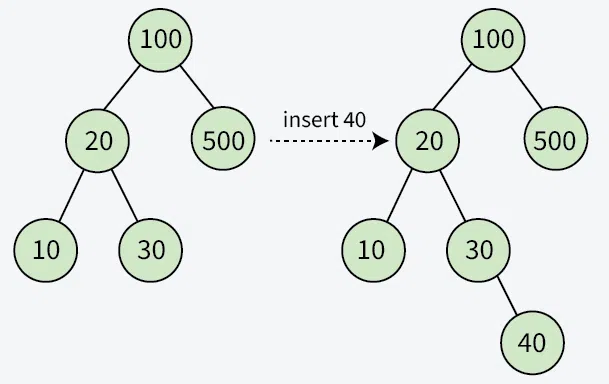
A new key is inserted at the position that maintains the BST property. We start from the root and move downward: if the key is smaller, go left; if larger, go right. We continue until we find an unoccupied spot where the node can be placed without violating the BST property, and insert it there as a new leaf.
Insertion in Binary Search Tree using Recursion:
C++ //Driver Code Starts #include <iostream> #include <queue> #include <vector> #include <algorithm> using namespace std; // Node structure class Node { public: int data; Node* left; Node* right; Node(int val) { data = val; left = right = nullptr; } }; int getHeight(Node* root, int h) { if (root == nullptr) return h - 1; return max(getHeight(root->left, h + 1), getHeight(root->right, h + 1)); } void levelOrder(Node* root) { queue<pair<Node*, int>> q; q.push({root, 0}); int lastLevel = 0; int height = getHeight(root, 0); while (!q.empty()) { auto top = q.front(); q.pop(); Node* node = top.first; int lvl = top.second; if (lvl > lastLevel) { cout << " "; lastLevel = lvl; } // all levels are printed if (lvl > height) break; // printing null node cout << (node->data == -1 ? "N" : to_string(node->data)) << " "; // null node has no children if (node->data == -1) continue; if (node->left == nullptr) q.push({new Node(-1), lvl + 1}); else q.push({node->left, lvl + 1}); if (node->right == nullptr) q.push({new Node(-1), lvl + 1}); else q.push({node->right, lvl + 1}); } } //Driver Code Ends Node* insert(Node* root, int key) { // If the tree is empty, return a new node if (root == nullptr) return new Node(key); // Otherwise, recur down the tree if (key < root->data) root->left = insert(root->left, key); else root->right = insert(root->right, key); // Return the (unchanged) node pointer return root; } //Driver Code Starts int main() { Node* root = nullptr; // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / \ // 15 30 root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 30); root = insert(root, 15); // print the level order // traversal of the BST levelOrder(root); } //Driver Code Ends //Driver Code Starts #include <stdio.h> #include <stdlib.h> // Node structure struct Node { int data; struct Node* left; struct Node* right; }; // Function prototypes struct Node* newNode(int val); struct Node* insert(struct Node* root, int key); void levelOrder(struct Node* root); int getHeight(struct Node* root, int h); // Queue node for level order traversal struct QueueNode { struct Node* node; int level; struct QueueNode* next; }; // Queue structure struct Queue { struct QueueNode* front; struct QueueNode* rear; }; // Create a new queue struct Queue* createQueue() { struct Queue* q = (struct Queue*)malloc(sizeof(struct Queue)); q->front = q->rear = NULL; return q; } // Enqueue node with level void enqueue(struct Queue* q, struct Node* node, int level) { struct QueueNode* temp = (struct QueueNode*)malloc(sizeof(struct QueueNode)); temp->node = node; temp->level = level; temp->next = NULL; if (q->rear == NULL) { q->front = q->rear = temp; return; } q->rear->next = temp; q->rear = temp; } // Dequeue node struct QueueNode* dequeue(struct Queue* q) { if (q->front == NULL) return NULL; struct QueueNode* temp = q->front; q->front = q->front->next; if (q->front == NULL) q->rear = NULL; return temp; } // Check if queue is empty int isEmpty(struct Queue* q) { return q->front == NULL; } // Function to get height of tree int getHeight(struct Node* root, int h) { if (root == NULL) return h - 1; int leftH = getHeight(root->left, h + 1); int rightH = getHeight(root->right, h + 1); return (leftH > rightH ? leftH : rightH); } // Level order traversal (prints N for null) void levelOrder(struct Node* root) { if (root == NULL) return; struct Queue* queue = createQueue(); enqueue(queue, root, 0); int lastLevel = 0; int height = getHeight(root, 0); while (!isEmpty(queue)) { struct QueueNode* top = dequeue(queue); struct Node* node = top->node; int lvl = top->level; free(top); if (lvl > lastLevel) { printf(" "); lastLevel = lvl; } if (lvl > height) break; if (node == NULL) { printf("N "); continue; } printf("%d ", node->data); enqueue(queue, node->left, lvl + 1); enqueue(queue, node->right, lvl + 1); } } //Driver Code Ends // Create a new node struct Node* newNode(int val) { struct Node* node = (struct Node*)malloc(sizeof(struct Node)); node->data = val; node->left = node->right = NULL; return node; } // Insert a node in BST struct Node* insert(struct Node* root, int key) { if (root == NULL) return newNode(key); if (key < root->data) root->left = insert(root->left, key); else if (key > root->data) root->right = insert(root->right, key); return root; } //Driver Code Starts int main() { struct Node* root = NULL; // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / // 15 root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 15); // Print the level order traversal levelOrder(root); return 0; } //Driver Code Ends //Driver Code Starts import java.util.LinkedList; import java.util.Queue; import java.util.List; import java.util.ArrayList; // Node structure class Node { int data; Node left, right; public Node(int val) { data = val; left = right = null; } } class GFG { static int getHeight( Node root, int h ) { if( root == null ) return h-1; return Math.max(getHeight(root.left, h+1), getHeight(root.right, h+1)); } static void levelOrder(Node root) { Queue<List<Object>> queue = new LinkedList<>(); queue.offer(List.of(root, 0)); int lastLevel = 0; // function to get the height of tree int height = getHeight(root, 0); // printing the level order of tree while( !queue.isEmpty()) { List<Object> top = queue.poll(); Node node = (Node) top.get(0); int lvl = (int) top.get(1); if( lvl > lastLevel ) { System.out.println(); lastLevel = lvl; } // all levels are printed if( lvl > height ) break; // printing null node System.out.print((node.data == -1 ? "N" : node.data) + " "); // null node has no children if( node.data == -1 ) continue; if( node.left == null ) queue.offer(List.of(new Node(-1), lvl+1)); else queue.offer(List.of(node.left, lvl+1)); if( node.right == null ) queue.offer(List.of(new Node(-1), lvl+1)); else queue.offer(List.of(node.right, lvl+1)); } } //Driver Code Ends static Node insert(Node root, int key) { // If the tree is empty, return a new node if (root == null) return new Node(key); // Otherwise, recur down the tree if (key < root.data) root.left = insert(root.left, key); else root.right = insert(root.right, key); // Return the (unchanged) node pointer return root; } //Driver Code Starts public static void main(String[] args) { Node root = null; // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / \ // 15 30 root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 30); root = insert(root, 15); // print the level order // traversal of the BST levelOrder(root); } } //Driver Code Ends #Driver Code Starts from collections import deque # Node structure class Node: def __init__(self, val): self.data = val self.left = None self.right = None def getHeight(root, h): if root is None: return h - 1 return max(getHeight(root.left, h + 1), getHeight(root.right, h + 1)) def levelOrder(root): queue = deque() queue.append((root, 0)) lastLevel = 0 height = getHeight(root, 0) while queue: node, lvl = queue.popleft() if lvl > lastLevel: print() lastLevel = lvl # all levels are printed if lvl > height: break # printing null node print("N" if node.data == -1 else node.data, end=" ") # null node has no children if node.data == -1: continue if node.left is None: queue.append((Node(-1), lvl + 1)) else: queue.append((node.left, lvl + 1)) if node.right is None: queue.append((Node(-1), lvl + 1)) else: queue.append((node.right, lvl + 1)) #Driver Code Ends def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.data: root.left = insert(root.left, key) else: root.right = insert(root.right, key) # Return the (unchanged) node pointer return root #Driver Code Starts # Create BST # 22 # / \ # 12 30 # / \ # 8 20 # / \ # 15 30 root = None root = insert(root, 22) root = insert(root, 12) root = insert(root, 30) root = insert(root, 8) root = insert(root, 20) root = insert(root, 30) root = insert(root, 15) # print the level order # traversal of the BST levelOrder(root) #Driver Code Ends //Driver Code Starts using System; using System.Collections.Generic; // Node structure class Node { public int data; public Node left, right; public Node(int val) { data = val; left = right = null; } } class GFG { static int getHeight(Node root, int h) { if (root == null) return h - 1; return Math.Max(getHeight(root.left, h + 1), getHeight(root.right, h + 1)); } static void levelOrder(Node root) { Queue<(Node, int)> queue = new Queue<(Node, int)>(); queue.Enqueue((root, 0)); int lastLevel = 0; int height = getHeight(root, 0); while (queue.Count > 0) { var (node, lvl) = queue.Dequeue(); if (lvl > lastLevel) { Console.WriteLine(); lastLevel = lvl; } // all levels are printed if (lvl > height) break; // printing null node Console.Write((node.data == -1 ? "N" : node.data.ToString()) + " "); // null node has no children if (node.data == -1) continue; if (node.left == null) queue.Enqueue((new Node(-1), lvl + 1)); else queue.Enqueue((node.left, lvl + 1)); if (node.right == null) queue.Enqueue((new Node(-1), lvl + 1)); else queue.Enqueue((node.right, lvl + 1)); } } //Driver Code Ends static Node insert(Node root, int key) { // If the tree is empty, return a new node if (root == null) return new Node(key); // Otherwise, recur down the tree if (key < root.data) root.left = insert(root.left, key); else root.right = insert(root.right, key); // Return the (unchanged) node pointer return root; } //Driver Code Starts public static void Main(string[] args) { Node root = null; // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / \ // 15 30 root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 30); root = insert(root, 15); // print the level order // traversal of the BST levelOrder(root); } } //Driver Code Ends //Driver Code Starts const Denque = require("denque"); // Node structure class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } function getHeight(root, h) { if (root === null) return h - 1; return Math.max(getHeight(root.left, h + 1), getHeight(root.right, h + 1)); } function levelOrder(root) { const queue = new Denque(); queue.push([root, 0]); let lastLevel = 0; const height = getHeight(root, 0); while (!queue.isEmpty()) { const [node, lvl] = queue.shift(); if (lvl > lastLevel) { console.log(); lastLevel = lvl; } // all levels are printed if (lvl > height) break; // printing null node process.stdout.write((node.data === -1 ? "N" : node.data) + " "); // null node has no children if (node.data === -1) continue; if (node.left === null) queue.push([new Node(-1), lvl + 1]); else queue.push([node.left, lvl + 1]); if (node.right === null) queue.push([new Node(-1), lvl + 1]); else queue.push([node.right, lvl + 1]); } } //Driver Code Ends function insert(root, key) { // If the tree is empty, return a new node if (root === null) return new Node(key); // Otherwise, recur down the tree if (key < root.data) root.left = insert(root.left, key); else root.right = insert(root.right, key); // Return the (unchanged) node pointer return root; } //Driver Code Starts // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / \ // 15 30 let root = null; root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 30); root = insert(root, 15); // print the level order // traversal of the BST levelOrder(root); //Driver Code Ends Output22 12 30 8 20 N 30 N N 15 N N N
Time Complexity: O(h)
- The worst-case time complexity of insert operations is O(h) where h is the height of the Binary Search Tree.
- In the worst case, we may have to travel from the root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of insertion operation may become O(n).
Auxiliary Space: O(h), due to recursive stack.
Insertion in Binary Search Tree using Iterative approach:
Instead of using recursion, we can also implement the insertion operation iteratively using a while loop. Below is the implementation using a while loop, using the same idea as above.
C++ //Driver Code Starts #include <iostream> #include <queue> #include <vector> #include <algorithm> using namespace std; // Node structure class Node { public: int data; Node* left; Node* right; Node(int item) { data = item; left = right = nullptr; } }; int getHeight(Node* root, int h) { if (root == nullptr) return h - 1; return max(getHeight(root->left, h + 1), getHeight(root->right, h + 1)); } void levelOrder(Node* root) { queue<pair<Node*, int>> queue; queue.push({root, 0}); int lastLevel = 0; int height = getHeight(root, 0); while (!queue.empty()) { auto top = queue.front(); queue.pop(); Node* node = top.first; int lvl = top.second; if (lvl > lastLevel) { cout << " "; lastLevel = lvl; } // all levels are printed if (lvl > height) break; // printing null node cout << (node->data == -1 ? "N" : to_string(node->data)) << " "; // null node has no children if (node->data == -1) continue; if (node->left == nullptr) queue.push({new Node(-1), lvl + 1}); else queue.push({node->left, lvl + 1}); if (node->right == nullptr) queue.push({new Node(-1), lvl + 1}); else queue.push({node->right, lvl + 1}); } } //Driver Code Ends Node* insert(Node* root, int key) { Node* temp = new Node(key); // If tree is empty if (root == nullptr) { return temp; } // Find the node who is going to // have the new node as its child Node* curr = root; while (curr != nullptr) { if (curr->data > key && curr->left != nullptr) { curr = curr->left; } else if (curr->data < key && curr->right != nullptr) { curr = curr->right; } else break; } // If key is smaller, make it left // child, else right child if (curr->data > key) { curr->left = temp; } else { curr->right = temp; } return root; } //Driver Code Starts int main() { Node* root = nullptr; // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / \ // 15 30 root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 30); root = insert(root, 15); // print the level order traversal of the BST levelOrder(root); } //Driver Code Ends //Driver Code Starts #include <stdio.h> #include <stdlib.h> // Node structure struct Node { int data; struct Node* left; struct Node* right; }; // Queue node for level order traversal struct QueueNode { struct Node* node; int level; struct QueueNode* next; }; // Queue structure struct Queue { struct QueueNode* front; struct QueueNode* rear; }; // Create a new queue struct Queue* createQueue() { struct Queue* q = (struct Queue*)malloc(sizeof(struct Queue)); q->front = q->rear = NULL; return q; } // Enqueue void enqueue(struct Queue* q, struct Node* node, int level) { struct QueueNode* temp = (struct QueueNode*)malloc(sizeof(struct QueueNode)); temp->node = node; temp->level = level; temp->next = NULL; if (q->rear == NULL) { q->front = q->rear = temp; return; } q->rear->next = temp; q->rear = temp; } // Dequeue struct QueueNode* dequeue(struct Queue* q) { if (q->front == NULL) return NULL; struct QueueNode* temp = q->front; q->front = q->front->next; if (q->front == NULL) q->rear = NULL; return temp; } // Check if queue is empty int isEmpty(struct Queue* q) { return q->front == NULL; } int getHeight(struct Node* root, int h) { if (root == NULL) return h - 1; int leftH = getHeight(root->left, h + 1); int rightH = getHeight(root->right, h + 1); return (leftH > rightH ? leftH : rightH); } void levelOrder(struct Node* root) { struct Queue* queue = createQueue(); enqueue(queue, root, 0); int lastLevel = 0; int height = getHeight(root, 0); while (!isEmpty(queue)) { struct QueueNode* top = dequeue(queue); struct Node* node = top->node; int lvl = top->level; free(top); if (lvl > lastLevel) { printf(" "); lastLevel = lvl; } // all levels are printed if (lvl > height) break; // printing null node if (node->data == -1) printf("N "); else printf("%d ", node->data); // null node has no children if (node->data == -1) continue; if (node->left == NULL) enqueue(queue, newNode(-1), lvl + 1); else enqueue(queue, node->left, lvl + 1); if (node->right == NULL) enqueue(queue, newNode(-1), lvl + 1); else enqueue(queue, node->right, lvl + 1); } } //Driver Code Ends // Create a new node struct Node* newNode(int item) { struct Node* node = (struct Node*)malloc(sizeof(struct Node)); node->data = item; node->left = node->right = NULL; return node; } struct Node* insert(struct Node* root, int key) { struct Node* temp = newNode(key); // If tree is empty if (root == NULL) return temp; // Find the node who is going to // have the new node as its child struct Node* curr = root; while (curr != NULL) { if (key < curr->data && curr->left != NULL) curr = curr->left; else if (key > curr->data && curr->right != NULL) curr = curr->right; else break; } // If key is smaller, make it left // child, else right child if (key < curr->data) curr->left = temp; else curr->right = temp; return root; } //Driver Code Starts int main() { struct Node* root = NULL; // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / \ // 15 30 root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 30); root = insert(root, 15); // print the level order // traversal of the BST levelOrder(root); } //Driver Code Ends //Driver Code Starts import java.util.LinkedList; import java.util.Queue; import java.util.List; import java.util.ArrayList; // Node structure class Node { int data; Node left, right; public Node(int item) { data = item; left = right = null; } } class GFG { static int getHeight( Node root, int h ) { if( root == null ) return h-1; return Math.max(getHeight(root.left, h+1), getHeight(root.right, h+1)); } static void levelOrder(Node root) { Queue<List<Object>> queue = new LinkedList<>(); queue.offer(List.of(root, 0)); int lastLevel = 0; // function to get the height of tree int height = getHeight(root, 0); // printing the level order of tree while( !queue.isEmpty()) { List<Object> top = queue.poll(); Node node = (Node) top.get(0); int lvl = (int) top.get(1); if( lvl > lastLevel ) { System.out.println(); lastLevel = lvl; } // all levels are printed if( lvl > height ) break; // printing null node System.out.print((node.data == -1 ? "N" : node.data) + " "); // null node has no children if( node.data == -1 ) continue; if( node.left == null ) queue.offer(List.of(new Node(-1), lvl+1)); else queue.offer(List.of(node.left, lvl+1)); if( node.right == null ) queue.offer(List.of(new Node(-1), lvl+1)); else queue.offer(List.of(node.right, lvl+1)); } } //Driver Code Ends static Node insert(Node root, int key) { Node temp = new Node(key); // If tree is empty if (root == null) { return temp; } // Find the node who is going to have // the new node temp as its child Node curr = root; while (curr != null) { if (curr.data > key && curr.left != null ) { curr = curr.left; } else if( curr.data < key && curr.right != null ) { curr = curr.right; } else break; } // If key is smaller, make it left // child, else right child if (curr.data > key) { curr.left = temp; } else { curr.right = temp; } return root; } //Driver Code Starts public static void main(String[] args) { Node root = null; // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / \ // 15 30 root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 30); root = insert(root, 15); // print the level order // traversal of the BST levelOrder(root); } } //Driver Code Ends #Driver Code Starts from collections import deque # Node structure class Node: def __init__(self, item): self.data = item self.left = None self.right = None def getHeight(root, h): if root is None: return h - 1 return max(getHeight(root.left, h + 1), getHeight(root.right, h + 1)) def levelOrder(root): queue = deque() queue.append((root, 0)) lastLevel = 0 height = getHeight(root, 0) while queue: node, lvl = queue.popleft() if lvl > lastLevel: print() lastLevel = lvl # all levels are printed if lvl > height: break # printing null node print("N" if node.data == -1 else node.data, end=" ") # null node has no children if node.data == -1: continue if node.left is None: queue.append((Node(-1), lvl + 1)) else: queue.append((node.left, lvl + 1)) if node.right is None: queue.append((Node(-1), lvl + 1)) else: queue.append((node.right, lvl + 1)) #Driver Code Ends def insert(root, key): temp = Node(key) # If tree is empty if root is None: return temp # Find the node who is going to have # the new node as its child curr = root while curr is not None: if curr.data > key and curr.left is not None: curr = curr.left elif curr.data < key and curr.right is not None: curr = curr.right else: break # If key is smaller, make it left # child, else right child if curr.data > key: curr.left = temp else: curr.right = temp return root #Driver Code Starts if __name__ == "__main__": # Create BST # 22 # / \ # 12 30 # / \ # 8 20 # / \ # 15 30 root = None root = insert(root, 22) root = insert(root, 12) root = insert(root, 30) root = insert(root, 8) root = insert(root, 20) root = insert(root, 30) root = insert(root, 15) # print the level order # traversal of the BST levelOrder(root) #Driver Code Ends //Driver Code Starts using System; using System.Collections.Generic; // Node structure class Node { public int data; public Node left, right; public Node(int item) { data = item; left = right = null; } } class GFG { static int getHeight(Node root, int h) { if (root == null) return h - 1; return Math.Max(getHeight(root.left, h + 1), getHeight(root.right, h + 1)); } static void levelOrder(Node root) { Queue<(Node, int)> queue = new Queue<(Node, int)>(); queue.Enqueue((root, 0)); int lastLevel = 0; int height = getHeight(root, 0); while (queue.Count > 0) { var (node, lvl) = queue.Dequeue(); if (lvl > lastLevel) { Console.WriteLine(); lastLevel = lvl; } // all levels are printed if (lvl > height) break; // printing null node Console.Write((node.data == -1 ? "N" : node.data.ToString()) + " "); // null node has no children if (node.data == -1) continue; if (node.left == null) queue.Enqueue((new Node(-1), lvl + 1)); else queue.Enqueue((node.left, lvl + 1)); if (node.right == null) queue.Enqueue((new Node(-1), lvl + 1)); else queue.Enqueue((node.right, lvl + 1)); } } //Driver Code Ends static Node insert(Node root, int key) { Node temp = new Node(key); // If tree is empty if (root == null) { return temp; } // Find the node who is going to // have the new node as its child Node curr = root; while (curr != null) { if (curr.data > key && curr.left != null) { curr = curr.left; } else if (curr.data < key && curr.right != null) { curr = curr.right; } else break; } // If key is smaller, make it left // child, else right child if (curr.data > key) { curr.left = temp; } else { curr.right = temp; } return root; } //Driver Code Starts public static void Main(string[] args) { Node root = null; // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / \ // 15 30 root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 30); root = insert(root, 15); // print the level order // traversal of the BST levelOrder(root); } } //Driver Code Ends //Driver Code Starts const Denque = require("denque"); // Node structure class Node { constructor(item) { this.data = item; this.left = null; this.right = null; } } function getHeight(root, h) { if (root === null) return h - 1; return Math.max(getHeight(root.left, h + 1), getHeight(root.right, h + 1)); } function levelOrder(root) { const queue = new Denque(); queue.push([root, 0]); let lastLevel = 0; // function to get the height of tree const height = getHeight(root, 0); // printing the level order of tree while (!queue.isEmpty()) { const [node, lvl] = queue.shift(); if (lvl > lastLevel) { console.log(); lastLevel = lvl; } // all levels are printed if (lvl > height) break; // printing null node process.stdout.write((node.data === -1 ? "N" : node.data) + " "); // null node has no children if (node.data === -1) continue; if (node.left === null) queue.push([new Node(-1), lvl + 1]); else queue.push([node.left, lvl + 1]); if (node.right === null) queue.push([new Node(-1), lvl + 1]); else queue.push([node.right, lvl + 1]); } } //Driver Code Ends function insert(root, key) { const temp = new Node(key); // If tree is empty if (root === null) return temp; // Find the node who is going to have // the new node as its child let curr = root; while (curr !== null) { if (curr.data > key && curr.left !== null) { curr = curr.left; } else if (curr.data < key && curr.right !== null) { curr = curr.right; } else break; } // If key is smaller, make it left // child, else right child if (curr.data > key) curr.left = temp; else curr.right = temp; return root; } //Driver Code Starts // Driver code // Create BST // 22 // / \ // 12 30 // / \ // 8 20 // / \ // 15 30 let root = null; root = insert(root, 22); root = insert(root, 12); root = insert(root, 30); root = insert(root, 8); root = insert(root, 20); root = insert(root, 30); root = insert(root, 15); // print the level order // traversal of the BST levelOrder(root); //Driver Code Ends Output22 12 30 8 20 N 30 N N 15 N N N
Time complexity: O(h), where h is the height of the tree.
Auxiliary space: O(1)
Related Links:
Explore
DSA Fundamentals
Data Structures
Algorithms
Advanced
Interview Preparation
Practice Problem
My Profile