Open In App

Insertion in a Binary Tree in level order

Last Updated : 04 Dec, 2025
Suggest changes
Share
411 Likes
Like
Report

Given a binary tree and a key, the task is to insert the key into the binary tree at the first position available in level order manner.

Examples:

Input: key = 12

insertion-in-a-binary-tree-in-level-order

Output:

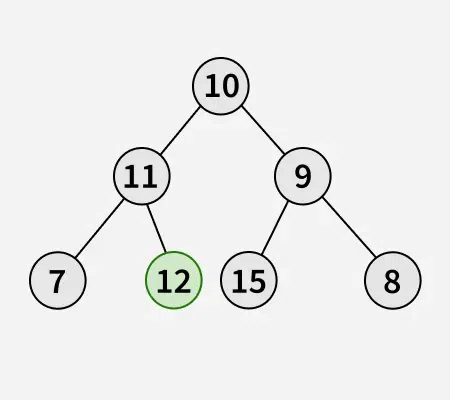
insertion-in-a-binary-tree-in-level-order-2


Explanation: Node with value 12 is inserted into the binary tree at the first position available in level order manner.

Approach:

The idea is to do an iterative level order traversal of the given tree using queue. If we find a node whose left child is empty, we make a new key as the left child of the node. Else if we find a node whose right child is empty, we make the new key as the right child. We keep traversing the tree until we find a node whose either left or right child is empty

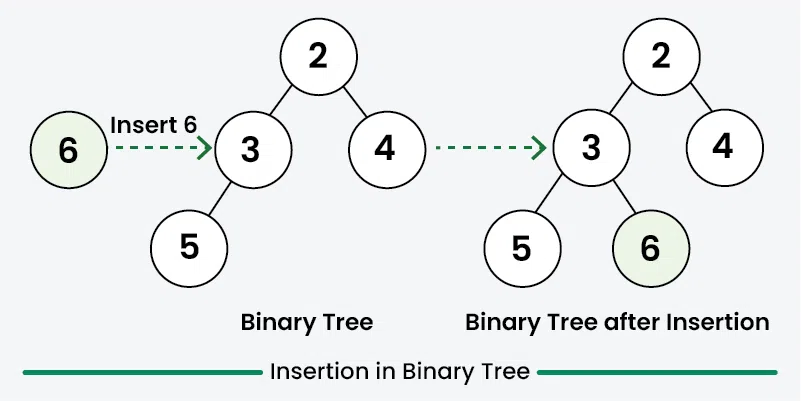
Insertion-in-Binary-Tree

Below is the implementation of the above approach: 

C++ 
// C++ program to insert element (in level order) // in Binary Tree #include <iostream> #include <queue> using namespace std; class Node { public:   int data;  Node* left;  Node* right; Node(int x) {  data = x;  left = right = nullptr;  } }; // Function to insert element in binary tree Node* InsertNode(Node* root, int data) {    // If the tree is empty, assign new  // node address to root  if (root == nullptr) {  root = new Node(data);  return root;  }  // Else, do level order traversal until we find an empty  // place, i.e. either left child or right child of some  // node is pointing to NULL.  queue<Node*> q;  q.push(root);  while (!q.empty()) {    // Fron a front element in queue  Node* curr = q.front();  q.pop();   // First check left if left is null   // insert node in left otherwise check for right  if (curr->left != nullptr)  q.push(curr->left);  else {  curr->left = new Node(data);  return root;  }   if (curr->right != nullptr)  q.push(curr->right);  else {  curr->right = new Node(data);  return root;  }  } } // Inorder traversal of a binary tree  void inorder(Node* curr) {  if (curr == nullptr)  return;  inorder(curr->left);  cout << curr->data << ' ';  inorder(curr->right); } int main() {    // Constructing the binary tree  // 10  // / \   // 11 9  // / / \  // 7 15 8    Node* root = new Node(10);  root->left = new Node(11);  root->right = new Node(9);  root->left->left = new Node(7);  root->right->left = new Node(15);  root->right->right = new Node(8);    int key = 12;  root = InsertNode(root, key);    // After insertion 12 in binary tree  // 10  // / \   // 11 9  // / \ / \  // 7 12 15 8  inorder(root);  return 0; }
Java 
// Java program to insert element (in level order) // in Binary Tree import java.util.LinkedList; import java.util.Queue; class Node {  int data;  Node left, right;    Node(int x) {  data = x;  left = right = null;  } } class GfG {    // Function to insert element   // in binary tree  static Node InsertNode(Node root, int data) {    // If the tree is empty, assign new node   // address to root  if (root == null) {  root = new Node(data);  return root;  }  // Else, do level order traversal until we find an empty  // place, i.e. either left child or right child of some  // node is pointing to NULL.  Queue<Node> q = new LinkedList<>();  q.add(root);  while (!q.isEmpty()) {    // Fron a front element in queue  Node curr = q.poll();  // First check left if left is null insert  // node in left otherwise check for right  if (curr.left != null)  q.add(curr.left);  else {  curr.left = new Node(data);  return root;  }  if (curr.right != null)  q.add(curr.right);  else {  curr.right = new Node(data);  return root;  }  }  return root;  }  // Inorder traversal of a binary tree  static void inorder(Node curr) {  if (curr == null)  return;  inorder(curr.left);  System.out.print(curr.data + " ");  inorder(curr.right);  }  public static void main(String[] args) {    // Constructing the binary tree  // 10  // / \   // 11 9  // / / \  // 7 15 8  Node root = new Node(10);  root.left = new Node(11);  root.right = new Node(9);  root.left.left = new Node(7);  root.right.left = new Node(15);  root.right.right = new Node(8);  int key = 12;  root = InsertNode(root, key);  // After insertion 12 in binary tree  // 10  // / \   // 11 9  // / \ / \  // 7 12 15 8  inorder(root);  } }
Python 
# Python program to insert element (in level order) # in Binary Tree from collections import deque class Node: def __init__(self, x): self.data = x self.left = None self.right = None # Function to insert element  # in binary tree def InsertNode(root, data): # If the tree is empty, assign new # node address to root if root is None: root = Node(data) return root # Else, do level order traversal until we find an empty # place, i.e. either left child or right child of some # node is pointing to NULL. q = deque() q.append(root) while q: # Fron a front element  # in queue curr = q.popleft() # First check left if left is null  # insert node in left otherwise check # for right if curr.left is not None: q.append(curr.left) else: curr.left = Node(data) return root if curr.right is not None: q.append(curr.right) else: curr.right = Node(data) return root # Inorder traversal of a binary tree def inorder(curr): if curr is None: return inorder(curr.left) print(curr.data, end=' ') inorder(curr.right) if __name__ == "__main__": # Constructing the binary tree # 10 # / \  # 11 9 # / / \ # 7 15 8 root = Node(10) root.left = Node(11) root.right = Node(9) root.left.left = Node(7) root.right.left = Node(15) root.right.right = Node(8) key = 12 root = InsertNode(root, key) # After insertion 12 in binary tree # 10 # / \  # 11 9 # / \ / \ # 7 12 15 8 inorder(root)
C# 
// C# program to insert element (in level order) // in Binary Tree using System; using System.Collections.Generic; class Node {  public int data;  public Node left, right;  public Node(int x) {  data = x;  left = right = null;  } } class GfG {    // Function to insert element in binary tree  static Node InsertNode(Node root, int data) {    // If the tree is empty, assign new node  // address to root  if (root == null) {  root = new Node(data);  return root;  }  // Else, do level order traversal until we find an empty  // place, i.e. either left child or right child of some  // node is pointing to NULL.  Queue<Node> q = new Queue<Node>();  q.Enqueue(root);  while (q.Count > 0) {    // Fron a front element in queue  Node curr = q.Dequeue();  // First check left if left is null  // insert node in left otherwise check   // for right  if (curr.left != null)  q.Enqueue(curr.left);  else {  curr.left = new Node(data);  return root;  }  if (curr.right != null)  q.Enqueue(curr.right);  else {  curr.right = new Node(data);  return root;  }  }  return root;  }  // Inorder traversal of a binary tree  static void inorder(Node curr) {  if (curr == null)  return;  inorder(curr.left);  Console.Write(curr.data + " ");  inorder(curr.right);  }  static void Main(string[] args) {    // Constructing the binary tree  // 10  // / \   // 11 9  // / / \  // 7 15 8  Node root = new Node(10);  root.left = new Node(11);  root.right = new Node(9);  root.left.left = new Node(7);  root.right.left = new Node(15);  root.right.right = new Node(8);  int key = 12;  root = InsertNode(root, key);  // After insertion 12 in binary tree  // 10  // / \   // 11 9  // / \ / \  // 7 12 15 8  inorder(root);  } }
JavaScript 
// JavaScript program to insert element  // (in level order) in Binary Tree class Node {  constructor(x) {  this.data = x;  this.left = null;  this.right = null;  } } // Function to insert element in binary tree function InsertNode(root, data) {  // If the tree is empty, assign new  // node address to root  if (root == null) {  root = new Node(data);  return root;  }  // Else, do level order traversal until we find an empty  // place, i.e. either left child or right child of some  // node is pointing to NULL.  let q = [];  q.push(root);  while (q.length > 0) {    let curr = q.shift();  // First check left if left is null   // insert node in left otherwise check for right  if (curr.left !== null)  q.push(curr.left);  else {  curr.left = new Node(data);  return root;  }  if (curr.right !== null)  q.push(curr.right);  else {  curr.right = new Node(data);  return root;  }  } } // Inorder traversal of a binary tree function inorder(curr) {  if (curr == null) return;  inorder(curr.left);  process.stdout.write(curr.data + ' ');  inorder(curr.right); } // Constructing the binary tree // 10 // / \  // 11 9 // / / \ // 7 15 8 let root = new Node(10); root.left = new Node(11); root.right = new Node(9); root.left.left = new Node(7); root.right.left = new Node(15); root.right.right = new Node(8); let key = 12; root = InsertNode(root, key); // After insertion 12 in binary tree // 10 // / \  // 11 9 // / \ / \ // 7 12 15 8 inorder(root);

Output
7 11 12 10 15 9 8

Time Complexity:  O(n) where n is the number of nodes.
Auxiliary Space: O(n)


Y

Yash Singla
Article Tags :

Explore

Lightbox