Implementation of DFS using adjacency matrix

Depth First Search (DFS) has been discussed in this article which uses adjacency list for the graph representation. In this article, adjacency matrix will be used to represent the graph.
Adjacency matrix representation: In adjacency matrix representation of a graph, the matrix mat[][] of size n*n (where n is the number of vertices) will represent the edges of the graph where mat[i][j] = 1 represents that there is an edge between the vertices i and j while mat[i][j] = 0 represents that there is no edge between the vertices i and j.
 

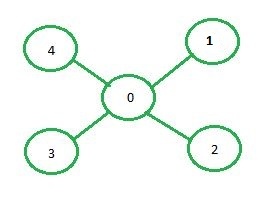
Below is the adjacency matrix representation of the graph shown in the above image: 
 

 0 1 2 3 4 0 0 1 1 1 1 1 1 0 0 0 0 2 1 0 0 0 0 3 1 0 0 0 0 4 1 0 0 0 0

Examples: 
 

Input: source = 0

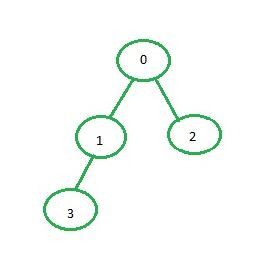
Output: 0 1 3 2 Input: source = 0

Output: 0 1 2 3 4

Approach: 
 

• Create a matrix of size n*n where every element is 0 representing there is no edge in the graph.
• Now, for every edge of the graph between the vertices i and j set mat[i][j] = 1.
• After the adjacency matrix has been created and filled, call the recursive function for the source i.e. vertex 0 that will recursively call the same function for all the vertices adjacent to it.
• Also, keep an array to keep track of the visited vertices i.e. visited[i] = true represents that vertex i has been visited before and the DFS function for some already visited node need not be called.

Below is the implementation of the above approach: 
 

// C++ implementation of the approach #include <bits/stdc++.h> using namespace std; // adjacency matrix vector<vector<int> > adj; // function to add edge to the graph void addEdge(int x, int y) {  adj[x][y] = 1;  adj[y][x] = 1; } // function to perform DFS on the graph void dfs(int start, vector<bool>& visited) {  // Print the current node  cout << start << " ";  // Set current node as visited  visited[start] = true;  // For every node of the graph  for (int i = 0; i < adj[start].size(); i++) {  // If some node is adjacent to the current node  // and it has not already been visited  if (adj[start][i] == 1 && (!visited[i])) {  dfs(i, visited);  }  } } int main() {  // number of vertices  int v = 5;  // number of edges  int e = 4;  // adjacency matrix  adj = vector<vector<int> >(v, vector<int>(v, 0));  addEdge(0, 1);  addEdge(0, 2);  addEdge(0, 3);  addEdge(0, 4);  // Visited vector to so that  // a vertex is not visited more than once  // Initializing the vector to false as no  // vertex is visited at the beginning  vector<bool> visited(v, false);  // Perform DFS  dfs(0, visited); } 

// Java implementation of the approach import java.io.*; class GFG {  // adjacency matrix  static int[][] adj;  // function to add edge to the graph  static void addEdge(int x, int y)  {  adj[x][y] = 1;  adj[y][x] = 1;  }  // function to perform DFS on the graph  static void dfs(int start, boolean[] visited)  {  // Print the current node  System.out.print(start + " ");  // Set current node as visited  visited[start] = true;  // For every node of the graph  for (int i = 0; i < adj[start].length; i++) {  // If some node is adjacent to the current node  // and it has not already been visited  if (adj[start][i] == 1 && (!visited[i])) {  dfs(i, visited);  }  }  }  public static void main(String[] args)  {  // number of vertices  int v = 5;  // number of edges  int e = 4;  // adjacency matrix  adj = new int[v][v];  addEdge(0, 1);  addEdge(0, 2);  addEdge(0, 3);  addEdge(0, 4);  // Visited vector to so that  // a vertex is not visited more than once  // Initializing the vector to false as no  // vertex is visited at the beginning  boolean[] visited = new boolean[v];  // Perform DFS  dfs(0, visited);  } } // This code is contributed by kdeepsingh2002 

# Python3 implementation of the approach  class Graph: adj = [] # Function to fill empty adjacency matrix def __init__(self, v, e): self.v = v self.e = e Graph.adj = [[0 for i in range(v)] for j in range(v)] # Function to add an edge to the graph def addEdge(self, start, e): # Considering a bidirectional edge Graph.adj[start][e] = 1 Graph.adj[e][start] = 1 # Function to perform DFS on the graph def DFS(self, start, visited): # Print current node print(start, end = ' ') # Set current node as visited visited[start] = True # For every node of the graph for i in range(self.v): # If some node is adjacent to the  # current node and it has not  # already been visited if (Graph.adj[start][i] == 1 and (not visited[i])): self.DFS(i, visited) # Driver code v, e = 5, 4 # Create the graph G = Graph(v, e) G.addEdge(0, 1) G.addEdge(0, 2) G.addEdge(0, 3) G.addEdge(0, 4) # Visited vector to so that a vertex # is not visited more than once # Initializing the vector to false as no # vertex is visited at the beginning visited = [False] * v # Perform DFS G.DFS(0, visited); # This code is contributed by ng24_7 

using System; using System.Collections.Generic; class GFG {  // adjacency matrix  static List<List<int>> adj;  // function to add edge to the graph  static void addEdge(int x, int y)  {  adj[x][y] = 1;  adj[y][x] = 1;  }  // function to perform DFS on the graph  static void dfs(int start, List<bool> visited)  {  // Print the current node  Console.Write(start + " ");  // Set current node as visited  visited[start] = true;  // For every node of the graph  for (int i = 0; i < adj[start].Count; i++)  {  // If some node is adjacent to the current node  // and it has not already been visited  if (adj[start][i] == 1 && (!visited[i]))  {  dfs(i, visited);  }  }  }  static void Main(string[] args) {  // number of vertices  int v = 5;  // number of edges  int e = 4;  // adjacency matrix  adj = new List<List<int>>(v);  for (int i = 0; i < v; i++)  {  adj.Add(new List<int>(v));  for (int j = 0; j < v; j++)  {  adj[i].Add(0);  }  }  addEdge(0, 1);  addEdge(0, 2);  addEdge(0, 3);  addEdge(0, 4);  // Visited vector to so that  // a vertex is not visited more than once  // Initializing the vector to false as no  // vertex is visited at the beginning  List<bool> visited = new List<bool>(v);  for (int i = 0; i < v; i++)  {  visited.Add(false);  }  // Perform DFS  dfs(0, visited);  } } // This code is contributed by Prince Kumar 

let ans=""; // JavaScript implementation of the Graph class class Graph {  constructor(v, e) {  this.v = v; // number of vertices  this.e = e; // number of edges  // initialize the adjacency matrix with 0s  this.adj = Array.from(Array(v), () => new Array(v).fill(0));  }  // function to add an edge to the graph  addEdge(start, end) {  // considering a bidirectional edge  this.adj[start][end] = 1;  this.adj[end][start] = 1;  }  // function to perform DFS on the graph  DFS(start, visited) {  // print the current node  ans = ans +start + " ";  // set current node as visited  visited[start] = true;  // for every node of the graph  for (let i = 0; i < this.v; i++) {  // if some node is adjacent to the current node  // and it has not already been visited  if (this.adj[start][i] === 1 && !visited[i]) {  this.DFS(i, visited);  }  }  } } // driver code const v = 5; // number of vertices const e = 4; // number of edges // create the graph const G = new Graph(v, e); G.addEdge(0, 1); G.addEdge(0, 2); G.addEdge(0, 3); G.addEdge(0, 4); // visited array to ensure that a vertex is not visited more than once // initializing the array to false as no vertex is visited at the beginning const visited = new Array(v).fill(false); // perform DFS G.DFS(0, visited); console.log(ans); 

0 1 2 3 4

The time complexity of the above implementation of DFS on an adjacency matrix is O(V^2), where V is the number of vertices in the graph. This is because for each vertex, we need to iterate through all the other vertices to check if they are adjacent or not.

The space complexity of this implementation is also O(V^2) because we are using an adjacency matrix to represent the graph, which requires V^2 space.