A Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices(V) and a set of edges(E). The graph is denoted by G(V, E).
Representations of Graph
Here are the two most common ways to represent a graph : For simplicity, we are going to consider only unweighted graphs in this post.
- Adjacency Matrix
- Adjacency List
Adjacency Matrix Representation
An adjacency matrix is a way of representing a graph as a boolean matrix of (0's and 1's).
Let's assume there are n vertices in the graph So, create a 2D matrix adjMat[n][n] having dimension n x n.
- If there is an edge from vertex i to j, mark adjMat[i][j] as 1.
- If there is no edge from vertex i to j, mark adjMat[i][j] as 0.
Representation of Undirected Graph as Adjacency Matrix:
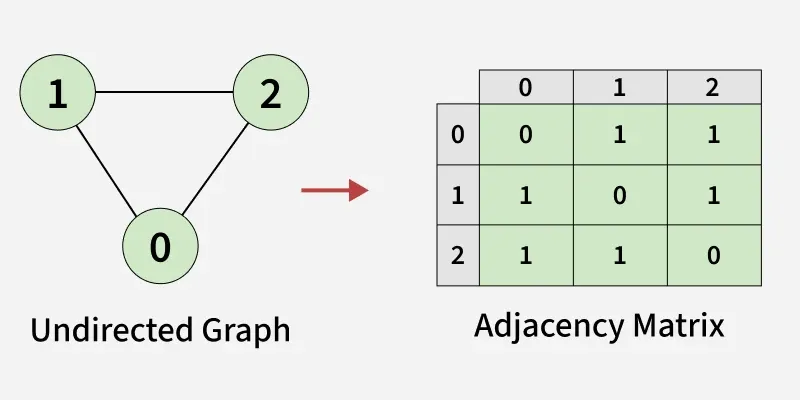
- We use an adjacency matrix to represent connections between vertices.
- Initially, the entire matrix is filled with 0s, meaning no edges exist.
- There is an edge between vertex 0 and vertex 1,so we set mat[0][1] = 1 and mat[1][0] = 1.
- There is an edge between vertex 0 and vertex 2,so we set mat[0][2] = 1 and mat[2][0] = 1.
- There is an edge between vertex 1 and vertex 2,so we set mat[1][2] = 1 and mat[2][1] = 1.
C++ #include <iostream> #include<vector> using namespace std; vector<vector<int>> createGraph(int V, vector<vector<int>> &edges) { vector<vector<int>> mat(V, vector<int>(V, 0)); // Add each edge to the adjacency matrix for (auto &it : edges) { int u = it[0]; int v = it[1]; mat[u][v] = 1; // since the graph is undirected mat[v][u] = 1; } return mat; } int main() { int V = 3; // List of edges (u, v) vector<vector<int>> edges = {{0, 1},{0, 2},{1, 2}}; // Build the graph using edges vector<vector<int>> mat = createGraph(V, edges); cout << "Adjacency Matrix Representation:" << endl; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) cout << mat[i][j] << " "; cout << endl; } return 0; } import java.util.ArrayList; import java.util.Collections; public class GFG { static ArrayList<ArrayList<Integer>> createGraph(int V, int[][] edges) { ArrayList<ArrayList<Integer>> mat = new ArrayList<>(); // Initialize the matrix with 0 for (int i = 0; i < V; i++) { ArrayList<Integer> row = new ArrayList<>(Collections.nCopies(V, 0)); mat.add(row); } // Add each edge to the adjacency matrix for (int[] it : edges) { int u = it[0]; int v = it[1]; mat.get(u).set(v, 1); // since the graph is undirected mat.get(v).set(u, 1); } return mat; } public static void main(String[] args) { int V = 3; // List of edges (u, v) int[][] edges = { {0, 1}, {0, 2}, {1, 2} }; // Build the graph using edges ArrayList<ArrayList<Integer>> mat = createGraph(V, edges); System.out.println("Adjacency Matrix Representation:"); for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) System.out.print(mat.get(i).get(j) + " "); System.out.println(); } } } def createGraph(V, edges): mat = [[0 for _ in range(V)] for _ in range(V)] # Add each edge to the adjacency matrix for it in edges: u = it[0] v = it[1] mat[u][v] = 1 # since the graph is undirected mat[v][u] = 1 return mat if __name__ == "__main__": V = 3 # List of edges (u, v) edges = [[0, 1], [0, 2], [1, 2]] # Build the graph using edges mat = createGraph(V, edges) print("Adjacency Matrix Representation:") for i in range(V): for j in range(V): print(mat[i][j], end=" ") print() using System; using System.Collections.Generic; class GFG { static List<List<int>> createGraph(int V, int[,] edges) { List<List<int>> mat = new List<List<int>>(); // Initialize the matrix with 0 for (int i = 0; i < V; i++) { List<int> row = new List<int>(new int[V]); mat.Add(row); } // Add each edge to the adjacency matrix for (int i = 0; i < edges.GetLength(0); i++) { int u = edges[i, 0]; int v = edges[i, 1]; mat[u][v] = 1; // since the graph is undirected mat[v][u] = 1; } return mat; } static void Main() { int V = 3; // List of edges (u, v) int[,] edges = {{0, 1},{0, 2},{1, 2}}; // Build the graph using edges List<List<int>> mat = createGraph(V, edges); Console.WriteLine("Adjacency Matrix Representation:"); for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) Console.Write(mat[i][j] + " "); Console.WriteLine(); } } } function createGraph(V, edges) { let mat = Array.from({ length: V }, () => Array(V).fill(0)); // Add each edge to the adjacency matrix for (let it of edges) { let u = it[0]; let v = it[1]; mat[u][v] = 1; // since the graph is undirected mat[v][u] = 1; } return mat; } //Driver Code let V = 3; // List of edges (u, v) let edges = [[0, 1],[0, 2],[1, 2]]; // Build the graph using edges let mat = createGraph(V, edges); console.log("Adjacency Matrix Representation:"); for (let i = 0; i < V; i++) { let row = ""; for (let j = 0; j < V; j++) row += mat[i][j] + " "; console.log(row.trim()); } OutputAdjacency Matrix Representation: 0 1 1 1 0 1 1 1 0
Representation of Directed Graph as Adjacency Matrix:
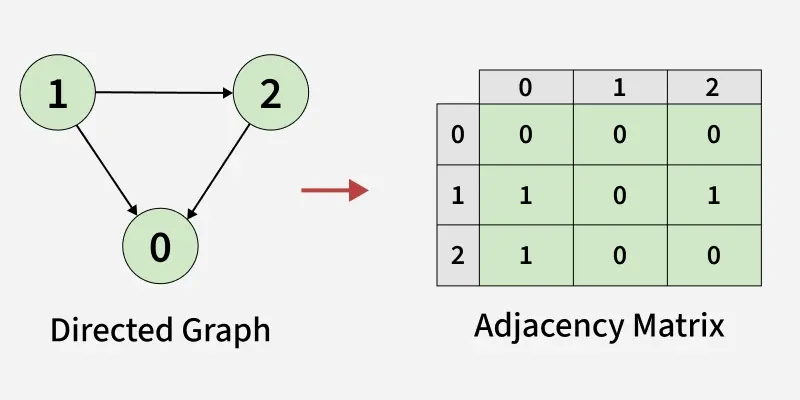
- Initially, the entire matrix is filled with 0s, meaning no edges exist.
- Unlike an undirected graph, we do not set mat[destination][source] because the edge goes in only one direction.
- There is an edge between vertex 1 and vertex 0,so we set mat[1][0] = 1.
- There is an edge between vertex 2 and vertex 0,so we set mat[2][0] = 1.
- There is an edge between vertex 1 and vertex 2,so we set mat[1][2] = 1.
C++ #include <iostream> #include<vector> using namespace std; vector<vector<int>> createGraph(int V, vector<vector<int>> &edges) { vector<vector<int>> mat(V, vector<int>(V, 0)); // Add each edge to the adjacency matrix for (auto &it : edges) { int u = it[0]; int v = it[1]; mat[u][v] = 1; } return mat; } int main() { int V = 3; // List of edges (u, v) vector<vector<int>> edges = {{1, 0},{2, 0},{1, 2}}; // Build the graph using edges vector<vector<int>> mat = createGraph(V, edges); cout << "Adjacency Matrix Representation:" << endl; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) cout << mat[i][j] << " "; cout << endl; } return 0; } import java.util.ArrayList; import java.util.Collections; public class GFG { static ArrayList<ArrayList<Integer>> createGraph(int V, int[][] edges) { ArrayList<ArrayList<Integer>> mat = new ArrayList<>(); // Initialize the matrix with 0 for (int i = 0; i < V; i++) { ArrayList<Integer> row = new ArrayList<>(Collections.nCopies(V, 0)); mat.add(row); } // Add each edge to the adjacency matrix for (int[] it : edges) { int u = it[0]; int v = it[1]; mat.get(u).set(v, 1); } return mat; } public static void main(String[] args) { int V = 3; // List of edges (u, v) int[][] edges = {{1, 0},{2, 0},{1, 2}}; // Build the graph using edges ArrayList<ArrayList<Integer>> mat = createGraph(V, edges); System.out.println("Adjacency Matrix Representation:"); for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) System.out.print(mat.get(i).get(j) + " "); System.out.println(); } } } def createGraph(V, edges): mat = [[0 for _ in range(V)] for _ in range(V)] # Add each edge to the adjacency matrix for it in edges: u = it[0] v = it[1] mat[u][v] = 1 return mat if __name__ == "__main__": V = 3 # List of edges (u, v) edges = [[1, 0], [2, 0], [1, 2]] # Build the graph using edges mat = createGraph(V, edges) print("Adjacency Matrix Representation:") for i in range(V): for j in range(V): print(mat[i][j], end=" ") print() using System; using System.Collections.Generic; class GFG { static List<List<int>> createGraph(int V, int[,] edges) { List<List<int>> mat = new List<List<int>>(); // Initialize the matrix with 0 for (int i = 0; i < V; i++) { List<int> row = new List<int>(new int[V]); mat.Add(row); } // Add each edge to the adjacency matrix for (int i = 0; i < edges.GetLength(0); i++) { int u = edges[i, 0]; int v = edges[i, 1]; mat[u][v] = 1; } return mat; } static void Main() { int V = 3; // List of edges (u, v) int[,] edges = {{1, 0},{2, 0},{1, 2}}; // Build the graph using edges List<List<int>> mat = createGraph(V, edges); Console.WriteLine("Adjacency Matrix Representation:"); for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) Console.Write(mat[i][j] + " "); Console.WriteLine(); } } } function createGraph(V, edges) { let mat = Array.from({ length: V }, () => Array(V).fill(0)); // Add each edge to the adjacency matrix for (let it of edges) { let u = it[0]; let v = it[1]; mat[u][v] = 1; } return mat; } //Driver Code let V = 3; // List of edges (u, v) let edges = [[1, 0], [2, 0], [1, 2]]; // Build the graph using edges let mat = createGraph(V, edges); console.log("Adjacency Matrix Representation:"); for (let i = 0; i < V; i++) { let row = ""; for (let j = 0; j < V; j++) row += mat[i][j] + " "; console.log(row.trim()); } OutputAdjacency Matrix Representation: 0 0 0 1 0 1 1 0 0
Adjacency List Representation
An array of Lists is used to store edges between two vertices. The size of array is equal to the number of vertices (i.e, n). Each index in this array represents a specific vertex in the graph. The entry at the index i of the array contains a linked list containing the vertices that are adjacent to vertex i. Let's assume there are n vertices in the graph So, create an array of list of size n as adjList[n].
- adjList[0] will have all the nodes which are connected (neighbour) to vertex 0.
- adjList[1] will have all the nodes which are connected (neighbour) to vertex 1 and so on.
Representation of Undirected Graph as Adjacency list:
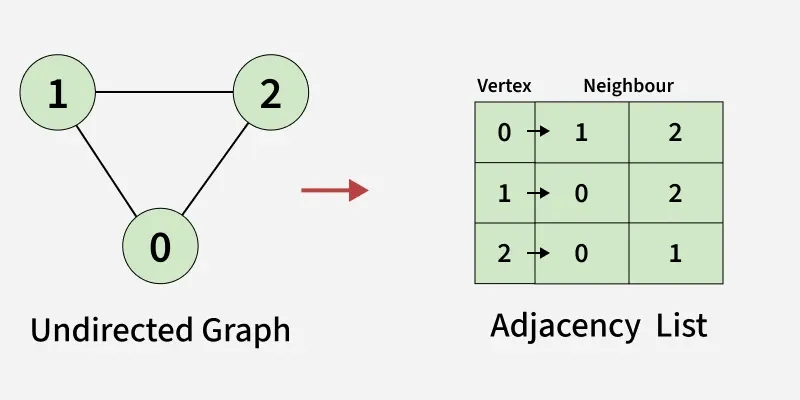
- We use an array of lists (or vector of lists) to represent the graph.
- The size of the array is equal to the number of vertices (here, 3).
- Each index in the array represents a vertex.
- Vertex 0 has two neighbours (1 and 2).
- Vertex 1 has two neighbours (0 and 2).
- Vertex 2 has two neighbours (0 and 1).
C++ #include <iostream> #include <vector> using namespace std; vector<vector<int>> createGraph(int V, vector<vector<int>> &edges) { vector<vector<int>> adj(V); // Add each edge to the adjacency list for (auto &it : edges) { int u = it[0]; int v = it[1]; adj[u].push_back(v); // since the graph is undirected adj[v].push_back(u); } return adj; } int main() { int V = 3; // List of edges (u, v) vector<vector<int>> edges = { {0, 1}, {0, 2}, {1, 2} }; // Build the graph using edges vector<vector<int>> adj = createGraph(V, edges); cout << "Adjacency List Representation:" << endl; for (int i = 0; i < V; i++) { // Print the vertex cout << i << ": "; for (int j : adj[i]) { // Print its adjacent cout << j << " "; } cout << endl; } return 0; } import java.util.ArrayList; public class GFG { static ArrayList<ArrayList<Integer>> createGraph(int V, int[][] edges) { ArrayList<ArrayList<Integer>> adj = new ArrayList<>(); for (int i = 0; i < V; i++) adj.add(new ArrayList<>()); // Add each edge to the adjacency list for (int i = 0; i < edges.length; i++) { int u = edges[i][0]; int v = edges[i][1]; adj.get(u).add(v); // since the graph is undirected adj.get(v).add(u); } return adj; } public static void main(String[] args) { int V = 3; // List of edges (u, v) int[][] edges = { {0, 1}, {0, 2}, {1, 2} }; // Build the graph using edges ArrayList<ArrayList<Integer>> adj = createGraph(V, edges); System.out.println("Adjacency List Representation:"); for (int i = 0; i < V; i++) { // Print the vertex System.out.print(i + ": "); for (int j : adj.get(i)) { // Print its adjacent System.out.print(j + " "); } System.out.println(); } } } def createGraph(V, edges): adj = [[] for _ in range(V)] # Add each edge to the adjacency list for it in edges: u = it[0] v = it[1] adj[u].append(v) # since the graph is undirected adj[v].append(u) return adj if __name__ == "__main__": V = 3 # List of edges (u, v) edges = [[0, 1], [0, 2], [1, 2]] # Build the graph using edges adj = createGraph(V, edges) print("Adjacency List Representation:") for i in range(V): # Print the vertex print(f"{i}:", end=" ") for j in adj[i]: # Print its adjacent print(j, end=" ") print() using System; using System.Collections.Generic; class GFG { static List<List<int>> createGraph(int V, int[,] edges) { List<List<int>> adj = new List<List<int>>(); for (int i = 0; i < V; i++) adj.Add(new List<int>()); // Add each edge to the adjacency list for (int i = 0; i < edges.GetLength(0); i++) { int u = edges[i, 0]; int v = edges[i, 1]; adj[u].Add(v); // since the graph is undirected adj[v].Add(u); } return adj; } static void Main() { int V = 3; // List of edges (u, v) int[,] edges = { { 0, 1 }, { 0, 2 }, { 1, 2 } }; // Build the graph using edges List<List<int>> adj = createGraph(V, edges); Console.WriteLine("Adjacency List Representation:"); for (int i = 0; i < V; i++) { // Print the vertex Console.Write(i + ": "); foreach (int j in adj[i]) { // Print its adjacent Console.Write(j + " "); } Console.WriteLine(); } } } function createGraph(V, edges) { let adj = Array.from({ length: V }, () => []); // Add each edge to the adjacency list for (let it of edges) { let u = it[0]; let v = it[1]; adj[u].push(v); // since the graph is undirected adj[v].push(u); } return adj; } //Driver Code let V = 3; // List of edges (u, v) let edges = [ [0, 1], [0, 2], [1, 2] ]; // Build the graph using edges let adj = createGraph(V, edges); console.log("Adjacency List Representation:"); for (let i = 0; i < V; i++) { // Print the vertex let row = i + ": "; for (let j of adj[i]) { // Print its adjacent row += j + " "; } console.log(row.trim()); } OutputAdjacency List Representation: 0: 1 2 1: 0 2 2: 0 1
Representation of Directed Graph as Adjacency list:
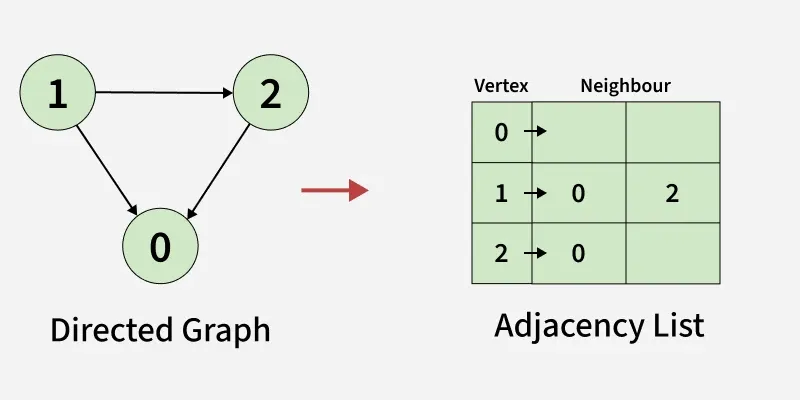
- We use an array of lists (or vector of lists) to represent the graph.
- The size of the array is equal to the number of vertices (here, 3).
- Each index in the array represents a vertex.
- Vertex 0 has no neighbours
- Vertex 1 has two neighbours (0 and 2).
- Vertex 2 has 1 neighbours (0).
C++ #include <iostream> #include <vector> using namespace std; vector<vector<int>> createGraph(int V, vector<vector<int>> &edges) { vector<vector<int>> adj(V); // Add each edge to the adjacency list for (auto &it : edges) { int u = it[0]; int v = it[1]; adj[u].push_back(v); } return adj; } int main() { int V = 3; // List of edges (u, v) vector<vector<int>> edges = { {1, 0}, {1, 2}, {2, 0} }; // Build the graph using edges vector<vector<int>> adj = createGraph(V, edges); cout << "Adjacency List Representation:" << endl; for (int i = 0; i < V; i++) { // Print the vertex cout << i << ": "; for (int j : adj[i]) { // Print its adjacent cout << j << " "; } cout << endl; } return 0; } import java.util.ArrayList; public class GFG { static ArrayList<ArrayList<Integer>> createGraph(int V, int[][] edges) { ArrayList<ArrayList<Integer>> adj = new ArrayList<>(); for (int i = 0; i < V; i++) adj.add(new ArrayList<>()); // Add each edge to the adjacency list for (int i = 0; i < edges.length; i++) { int u = edges[i][0]; int v = edges[i][1]; adj.get(u).add(v); } return adj; } public static void main(String[] args) { int V = 3; // List of edges (u, v) int[][] edges = { {1, 0}, {1, 2}, {2, 0} }; // Build the graph using edges ArrayList<ArrayList<Integer>> adj = createGraph(V, edges); System.out.println("Adjacency List Representation:"); for (int i = 0; i < V; i++) { // Print the vertex System.out.print(i + ": "); for (int j : adj.get(i)) { // Print its adjacent System.out.print(j + " "); } System.out.println(); } } } def createGraph(V, edges): adj = [[] for _ in range(V)] # Add each edge to the adjacency list for it in edges: u = it[0] v = it[1] adj[u].append(v) return adj if __name__ == "__main__": V = 3 # List of edges (u, v) edges = [[1, 0], [1, 2], [2, 0]] # Build the graph using edges adj = createGraph(V, edges) print("Adjacency List Representation:") for i in range(V): # Print the vertex print(f"{i}:", end=" ") for j in adj[i]: # Print its adjacent print(j, end=" ") print() using System; using System.Collections.Generic; class GFG { static List<List<int>> createGraph(int V, int[,] edges) { List<List<int>> adj = new List<List<int>>(); for (int i = 0; i < V; i++) adj.Add(new List<int>()); // Add each edge to the adjacency list for (int i = 0; i < edges.GetLength(0); i++) { int u = edges[i, 0]; int v = edges[i, 1]; adj[u].Add(v); } return adj; } static void Main() { int V = 3; // List of edges (u, v) int[,] edges = { {1, 0}, {1, 2}, {2, 0} }; // Build the graph using edges List<List<int>> adj = createGraph(V, edges); Console.WriteLine("Adjacency List Representation:"); for (int i = 0; i < V; i++) { // Print the vertex Console.Write(i + ": "); foreach (int j in adj[i]) { // Print its adjacent Console.Write(j + " "); } Console.WriteLine(); } } } function createGraph(V, edges) { let adj = Array.from({ length: V }, () => []); // Add each edge to the adjacency list for (let it of edges) { let u = it[0]; let v = it[1]; adj[u].push(v); } return adj; } //Driver Code let V = 3; // List of edges (u, v) let edges = [ [1, 0], [1, 2], [2, 0] ]; // Build the graph using edges let adj = createGraph(V, edges); console.log("Adjacency List Representation:"); for (let i = 0; i < V; i++) { // Print the vertex let row = i + ": "; for (let j of adj[i]) { // Print its adjacent row += j + " "; } console.log(row.trim()); } OutputAdjacency List Representation: 0: 1: 0 2 2: 0
Explore
DSA Fundamentals
Data Structures
Algorithms
Advanced
Interview Preparation
Practice Problem
My Profile