Construct Complete Binary Tree from its Linked List Representation

Last Updated : 19 Sep, 2024

Given the Linked List Representation of a Complete Binary Tree, the task is to construct the complete binary tree. The complete binary tree is represented as a linked list in a way where if the root node is stored at position i, its left, and right children are stored at position 2*i+1, and 2*i+2 respectively.

Examples:

Input: 1->2->3>4->5
Output:

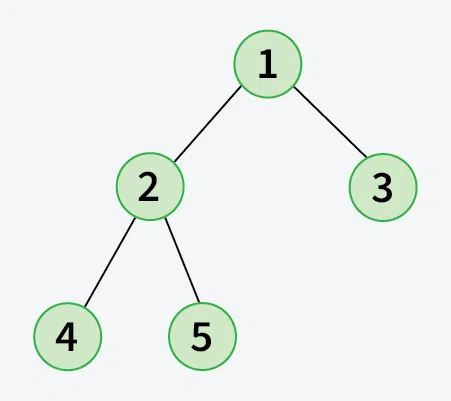
Input: 10->12->15->25->30->36
Output:

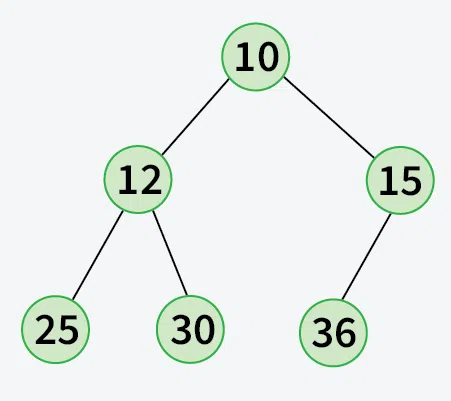
[Expected Approach] Using Level Order Traversal - O(n) Time and O(n) Space:

We are mainly given level order traversal in sequential form. Head of linked list is always the root of the tree. The first node as root and that the next two nodes are left and right children of root. So we know partial Binary Tree.
The idea is to do Level order traversal of the partially built Binary Tree using queue and traverse the linked list at the same time. At every step, we take the parent node from queue, make next two nodes of linked list as children of the parent node, and push the next two nodes to queue.

Below is the implementation of the above approach:

C++

// C++ program to create a Complete Binary tree // from its Linked List Representation #include <iostream> #include <queue> using namespace std; class Lnode { public:  int data;  Lnode* next;  Lnode(int value) {  data = value;  next = nullptr;  } }; class Tnode { public:  int data;  Tnode* left;  Tnode* right;  Tnode(int value) {  data = value;  left = right = nullptr;  } }; // Converts a given linked list representing a complete  // binary tree into the linked representation of a binary tree. Tnode* convert(Lnode* head) {  if (head == nullptr) {  return nullptr;  }  // Queue to store the parent nodes  queue<Tnode*> q;  // The first node is always the root node,  // and add it to the queue  Tnode* root = new Tnode(head->data);  q.push(root);  // Move the pointer to the next node  head = head->next;  // Until the end of the linked list is reached,   // do the following steps  while (head) {    // Take the parent node from the queue   // and remove it from the queue  Tnode* parent = q.front();  q.pop();  // Take the next two nodes from the linked list  Tnode* leftChild = nullptr;  Tnode* rightChild = nullptr;  // Create left child  if (head) {  leftChild = new Tnode(head->data);  q.push(leftChild);  head = head->next;  }  // Create right child  if (head) {  rightChild = new Tnode(head->data);  q.push(rightChild);  head = head->next;  }  // Assign the left and right children of the parent  parent->left = leftChild;  parent->right = rightChild;  }  return root; } // Level Order Traversal of the binary tree void levelOrderTraversal(Tnode* root) {  if (root == nullptr) {  return;  }  // Queue to hold nodes at each level  queue<Tnode*> q;  q.push(root);  while (!q.empty()) {  Tnode* currNode = q.front();  q.pop();  // Print the current node's data  cout << currNode->data << " ";  // Push the left and right children   // of the current node to the queue  if (currNode->left) {  q.push(currNode->left);  }  if (currNode->right) {  q.push(currNode->right);  }  } } int main() {    // Create linked list : 10->12->15->25->30->36  Lnode* head = new Lnode(10);  head->next = new Lnode(12);  head->next->next = new Lnode(15);  head->next->next->next = new Lnode(25);  head->next->next->next->next = new Lnode(30);  head->next->next->next->next->next = new Lnode(36);     Tnode* root = convert(head);  levelOrderTraversal(root);  return 0; }

Java

// Java program to create a Complete Binary tree // from its Linked List Representation import java.util.LinkedList; import java.util.Queue; class Lnode {  int data;  Lnode next;    Lnode(int value) {  data = value;  next = null;  } } class Tnode {  int data;  Tnode left, right;    Tnode(int value) {  data = value;  left = null;  right = null;  } } class GfG {    // Converts a given linked list representing a complete binary tree into the  // linked representation of a binary tree.  static Tnode convert(Lnode head) {  if (head == null) {  return null;  }  // Queue to store the parent nodes  Queue<Tnode> q = new LinkedList<>();  // The first node is always the root node,  // and add it to the queue  Tnode root = new Tnode(head.data);  q.add(root);  // Move the pointer to the next node  head = head.next;  // Until the end of the linked list is reached,  // do the following steps  while (head != null) {    // Take the parent node from the queue  // and remove it from the queue  Tnode parent = q.poll();  Tnode leftChild = null, rightChild = null;  // Create left child  if (head != null) {  leftChild = new Tnode(head.data);  q.add(leftChild);  head = head.next;  }  // Create right child  if (head != null) {  rightChild = new Tnode(head.data);  q.add(rightChild);  head = head.next;  }  // Assign the left and right children of the parent  parent.left = leftChild;  parent.right = rightChild;  }  return root;  }  // Level Order Traversal of the binary tree  static void levelOrderTraversal(Tnode root) {  if (root == null) {  return;  }  // Queue to hold nodes at each level  Queue<Tnode> q = new LinkedList<>();  q.add(root);  while (!q.isEmpty()) {  Tnode currNode = q.poll();  // Print the current node's data  System.out.print(currNode.data + " ");  // Push the left and right children  // of the current node to the queue  if (currNode.left != null) {  q.add(currNode.left);  }  if (currNode.right != null) {  q.add(currNode.right);  }  }  }  public static void main(String[] args) {    // Create linked list : 10->12->15->25->30->36  Lnode head = new Lnode(10);  head.next = new Lnode(12);  head.next.next = new Lnode(15);  head.next.next.next = new Lnode(25);  head.next.next.next.next = new Lnode(30);  head.next.next.next.next.next = new Lnode(36);  Tnode root = convert(head);  levelOrderTraversal(root);  } }

Python

# Python program to create a Complete Binary tree # from its Linked List Representation from collections import deque class Lnode: def __init__(self, value): self.data = value self.next = None class Tnode: def __init__(self, value): self.data = value self.left = None self.right = None # Converts a given linked list representing a complete # binary tree into the linked representation of a binary tree. def convert(head): if not head: return None # Queue to store the parent nodes q = deque() # The first node is always the root node, # and add it to the queue root = Tnode(head.data) q.append(root) # Move the pointer to the next node head = head.next # Until the end of the linked list is reached, # do the following steps while head: # Take the parent node from the queue # and remove it from the queue parent = q.popleft() leftChild = None rightChild = None # Create left child if head: leftChild = Tnode(head.data) q.append(leftChild) head = head.next # Create right child if head: rightChild = Tnode(head.data) q.append(rightChild) head = head.next # Assign the left and right children of the parent parent.left = leftChild parent.right = rightChild return root # Level Order Traversal of the binary tree def levelOrderTraversal(root): if not root: return # Queue to hold nodes at each level q = deque() q.append(root) while q: currNode = q.popleft() # Print the current node's data print(currNode.data, end=" ") # Push the left and right children # of the current node to the queue if currNode.left: q.append(currNode.left) if currNode.right: q.append(currNode.right) if __name__ == "__main__": # Create linked list : 10->12->15->25->30->36 head = Lnode(10) head.next = Lnode(12) head.next.next = Lnode(15) head.next.next.next = Lnode(25) head.next.next.next.next = Lnode(30) head.next.next.next.next.next = Lnode(36) root = convert(head) levelOrderTraversal(root)

// C# program to create a Complete Binary tree // from its Linked List Representation using System; using System.Collections.Generic; class Lnode {  public int data;  public Lnode next;  public Lnode(int value) {  data = value;  next = null;  } } class Tnode {  public int data;  public Tnode left, right;  public Tnode(int value) {  data = value;  left = null;  right = null;  } } class GfG {    // Converts a given linked list representing a complete binary tree into the  // linked representation of a binary tree.  static Tnode convert(Lnode head) {  if (head == null) {  return null;  }  // Queue to store the parent nodes  Queue<Tnode> q = new Queue<Tnode>();  // The first node is always the root node,  // and add it to the queue  Tnode root = new Tnode(head.data);  q.Enqueue(root);  // Move the pointer to the next node  head = head.next;  // Until the end of the linked list is reached,  // do the following steps  while (head != null) {    // Take the parent node from the queue  // and remove it from the queue  Tnode parent = q.Dequeue();  Tnode leftChild = null, rightChild = null;  // Create left child  if (head != null) {  leftChild = new Tnode(head.data);  q.Enqueue(leftChild);  head = head.next;  }  // Create right child  if (head != null) {  rightChild = new Tnode(head.data);  q.Enqueue(rightChild);  head = head.next;  }  // Assign the left and right children  // of the parent  parent.left = leftChild;  parent.right = rightChild;  }  return root;  }  // Level Order Traversal of the binary tree  static void LevelOrderTraversal(Tnode root) {  if (root == null) {  return;  }  // Queue to hold nodes at each level  Queue<Tnode> q = new Queue<Tnode>();  q.Enqueue(root);  while (q.Count > 0) {  Tnode currNode = q.Dequeue();  // Print the current node's data  Console.Write(currNode.data + " ");  // Push the left and right children  // of the current node to the queue  if (currNode.left != null) {  q.Enqueue(currNode.left);  }  if (currNode.right != null) {  q.Enqueue(currNode.right);  }  }  }  static void Main(string[] args) {    // Create linked list : 10->12->15->25->30->36  Lnode head = new Lnode(10);  head.next = new Lnode(12);  head.next.next = new Lnode(15);  head.next.next.next = new Lnode(25);  head.next.next.next.next = new Lnode(30);  head.next.next.next.next.next = new Lnode(36);  Tnode root = convert(head);  LevelOrderTraversal(root);  } }

JavaScript

// JavaScript program to create a Complete Binary tree // from its Linked List Representation // Linked list node class class Lnode {  constructor(value) {  this.data = value;  this.next = null;  } } // Binary tree node class class Tnode {  constructor(value) {  this.data = value;  this.left = null;  this.right = null;  } } // Converts a given linked list representing a  // complete binary tree into the linked representation of a binary tree. function convert(head) {  if (head === null) {  return null;  }  // Queue to store the parent nodes  let q = [];  // The first node is always the root node,  // and add it to the queue  let root = new Tnode(head.data);  q.push(root);  // Move the pointer to the next node  head = head.next;  // Until the end of the linked list is reached,  // do the following steps  while (head) {    // Take the parent node from the queue  // and remove it from the queue  let parent = q.shift();  let leftChild = null;  let rightChild = null;  // Create left child  if (head) {  leftChild = new Tnode(head.data);  q.push(leftChild);  head = head.next;  }  // Create right child  if (head) {  rightChild = new Tnode(head.data);  q.push(rightChild);  head = head.next;  }  // Assign the left and right   // children of the parent  parent.left = leftChild;  parent.right = rightChild;  }  return root; } // Level Order Traversal of the binary tree function levelOrderTraversal(root) {  if (root === null) {  return;  }  // Queue to hold nodes at each level  let q = [];  q.push(root);  while (q.length > 0) {  let currNode = q.shift();  // Print the current node's data  console.log(currNode.data + " ");  // Push the left and right children  // of the current node to the queue  if (currNode.left) {  q.push(currNode.left);  }  if (currNode.right) {  q.push(currNode.right);  }  } } // Create linked list : 10->12->15->25->30->36 let head = new Lnode(10); head.next = new Lnode(12); head.next.next = new Lnode(15); head.next.next.next = new Lnode(25); head.next.next.next.next = new Lnode(30); head.next.next.next.next.next = new Lnode(36); let root = convert(head); levelOrderTraversal(root);

Output

10 12 15 25 30 36

Time Complexity: O(n), where n is the number of nodes.
Auxiliary Space: O(n), The queue stores at most n/2 nodes at any point, since for every node processed, its children are added to the queue. Therefore, the maximum space used by the queue is O(n).