Eulerian path and circuit for undirected graph

Given an undirected connected graph with v nodes, and e edges, with adjacency list adj. We need to write a function that returns 2 if the graph contains an eulerian circuit or cycle, else if the graph contains an eulerian path, returns 1, otherwise, returns 0.

A graph is said to be Eulerian if it contains an Eulerian Cycle, a cycle that visits every edge exactly once and starts and ends at the same vertex.
If a graph contains an Eulerian Path, a path that visits every edge exactly once but starts and ends at different vertices, it is called Semi-Eulerian.

Examples:

Input:

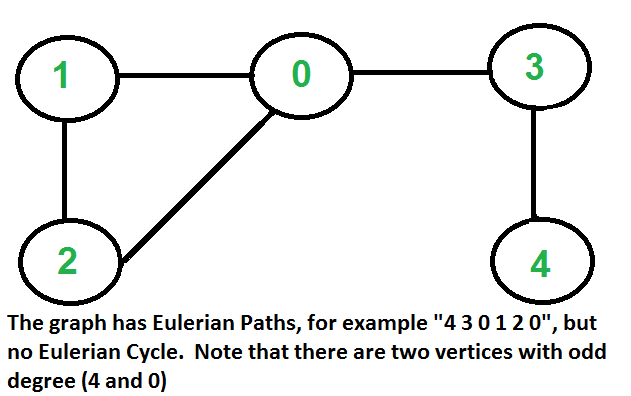
Output: 1

Input:

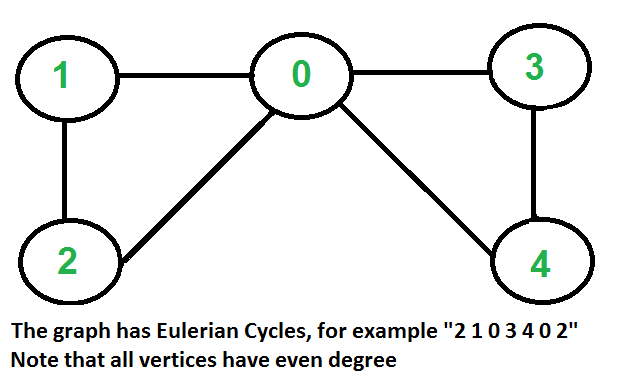
Output: 2

Input:

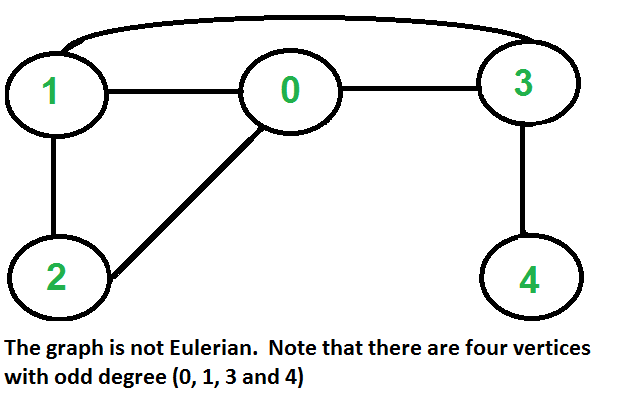
Output: 0

The problem can be framed as follows: "Is it possible to draw a graph without lifting your pencil from the paper and without retracing any edge?"
At first glance, this may seem similar to the Hamiltonian Path problem, which is NP-complete for general graphs. However, determining whether a graph has an Eulerian Path or Cycle is much more efficient: It can be solved in O(v + e) time.

Approach:

The idea is to use some key properties of undirected graphs that help determine whether they are Eulerian (i.e., contain an Eulerian Path or Cycle) or not.

Eulerian Cycle

A graph has an Eulerian Cycle if and only if the below two conditions are true

• All vertices with non-zero degree are part of a single connected component. (We ignore isolated vertices— those with zero degree — as they do not affect the cycle.)
• Every vertex in the graph has an even degree.

Eulerian Path

A graph has an Eulerian Path if and only if the below two conditions are true

• All vertices with non-zero degree must belong to the same connected component. (Same as Eulerian Cycle)
• Exactly Zero or Two Vertices with Odd Degree:
  • If zero vertices have odd degree → Eulerian Cycle exists (which is also a path).
  • If two vertices have odd degree → Eulerian Path exists (but not a cycle).
  • If one vertex has odd degree → Not possible in an undirected graph. (Because the sum of all degrees in an undirected graph is always even.)

Note: A graph with no edges is trivially Eulerian. There are no edges to traverse, so by definition, it satisfies both Eulerian Path and Cycle conditions.

How Does This Work? 

• In an Eulerian Path, whenever we enter a vertex (except start and end), we must also leave it. So all intermediate vertices must have even degree.
• In an Eulerian Cycle, since we start and end at the same vertex, every vertex must have even degree. This ensures that every entry into a vertex can be paired with an exit.

Steps to implement the above idea:

• Create an adjacency list to represent the graph and initialize a visited array for DFS traversal.
• Perform DFS starting from the first vertex having non-zero degree to check graph connectivity.
• After DFS, ensure all non-zero degree vertices were visited to confirm the graph is connected.
• Count the number of vertices with odd degree to classify the graph as Eulerian or not.
• If all degrees are even, the graph has an Eulerian Circuit; if exactly two are odd, it's a Path.
• If more than two vertices have odd degree or graph isn't connected, it's not Eulerian.
• Return 2 for Circuit, 1 for Path, and 0 when graph fails Eulerian conditions.

// C++ program to check whether a graph is // Eulerian Path, Eulerian Circuit, or neither #include <bits/stdc++.h> using namespace std; // DFS to check connectivity, excluding zero-degree vertices void dfs(int node, vector<int> adj[], vector<bool> &visited) {  visited[node] = true;  for (int neighbor : adj[node]) {  if (!visited[neighbor]) {  dfs(neighbor, adj, visited);  }  } } // Function to check Eulerian Path or Circuit int isEulerCircuit(int v, vector<int> adj[]) {  vector<bool> visited(v, false);  // Find first vertex with non-zero degree  int start = -1;  for (int i = 0; i < v; i++) {  if (adj[i].size() > 0) {  start = i;  break;  }  }  // No edges: graph is trivially Eulerian  if (start == -1) {  return 2;  }  // DFS from the first non-zero degree vertex  dfs(start, adj, visited);  // Check if all non-zero degree vertices are connected  for (int i = 0; i < v; i++) {  if (adj[i].size() > 0 && !visited[i]) {  return 0; // Not connected  }  }  // Count vertices with odd degree  int odd = 0;  for (int i = 0; i < v; i++) {  if (adj[i].size() % 2 != 0) {  odd++;  }  }  // Apply Eulerian rules  if (odd == 0) {  return 2;   } else if (odd == 2) {  return 1;   } else {  return 0;   } } // Driver code int main() {    int v = 5;  vector<int> adj[5] = {{1, 2, 3}, {0, 2},   {1, 0}, {0, 4}, {3}};  cout << isEulerCircuit(v, adj);  return 0; } 

// Java program to check whether a graph is // Eulerian Path, Eulerian Circuit, or neither import java.util.*; class GfG {  // DFS to check connectivity, excluding zero-degree vertices  static void dfs(int node, List<Integer>[] adj, boolean[] visited) {  visited[node] = true;  for (int neighbor : adj[node]) {  if (!visited[neighbor]) {  dfs(neighbor, adj, visited);  }  }  }  // Function to check Eulerian Path or Circuit  static int isEulerCircuit(int v, List<Integer>[] adj) {  boolean[] visited = new boolean[v];  // Find first vertex with non-zero degree  int start = -1;  for (int i = 0; i < v; i++) {  if (adj[i].size() > 0) {  start = i;  break;  }  }  // No edges: graph is trivially Eulerian  if (start == -1) {  return 2;  }  // DFS from the first non-zero degree vertex  dfs(start, adj, visited);  // Check if all non-zero degree vertices are connected  for (int i = 0; i < v; i++) {  if (adj[i].size() > 0 && !visited[i]) {  return 0; // Not connected  }  }  // Count vertices with odd degree  int odd = 0;  for (int i = 0; i < v; i++) {  if (adj[i].size() % 2 != 0) {  odd++;  }  }  // Apply Eulerian rules  if (odd == 0) {  return 2;   } else if (odd == 2) {  return 1;   } else {  return 0;   }  }  public static void main(String[] args) {  int v = 5;  List<Integer>[] adj = new ArrayList[v];  for (int i = 0; i < v; i++) {  adj[i] = new ArrayList<>();  }  adj[0].addAll(Arrays.asList(1, 2, 3));  adj[1].addAll(Arrays.asList(0, 2));  adj[2].addAll(Arrays.asList(1, 0));  adj[3].addAll(Arrays.asList(0, 4));  adj[4].addAll(Arrays.asList(3));  System.out.println(isEulerCircuit(v, adj));  } } 

# Python program to check whether a graph is # Eulerian Path, Eulerian Circuit, or neither # DFS to check connectivity, excluding zero-degree vertices def dfs(node, adj, visited): visited[node] = True for neighbor in adj[node]: if not visited[neighbor]: dfs(neighbor, adj, visited) # Function to check Eulerian Path or Circuit def isEulerCircuit(v, adj): visited = [False] * v # Find first vertex with non-zero degree start = -1 for i in range(v): if len(adj[i]) > 0: start = i break # No edges: graph is trivially Eulerian if start == -1: return 2 # DFS from the first non-zero degree vertex dfs(start, adj, visited) # Check if all non-zero degree vertices are connected for i in range(v): if len(adj[i]) > 0 and not visited[i]: return 0 # Not connected # Count vertices with odd degree odd = 0 for i in range(v): if len(adj[i]) % 2 != 0: odd += 1 # Apply Eulerian rules if odd == 0: return 2 elif odd == 2: return 1 else: return 0 if __name__ == "__main__": v = 5 adj = [ [1, 2, 3], [0, 2], [1, 0], [0, 4], [3] ] print(isEulerCircuit(v, adj)) 

// C# program to check whether a graph is // Eulerian Path, Eulerian Circuit, or neither using System; using System.Collections.Generic; class GfG {  // DFS to check connectivity, excluding zero-degree vertices  static void dfs(int node, List<int>[] adj, bool[] visited) {  visited[node] = true;  foreach (int neighbor in adj[node]) {  if (!visited[neighbor]) {  dfs(neighbor, adj, visited);  }  }  }  // Function to check Eulerian Path or Circuit  static int isEulerCircuit(int v, List<int>[] adj) {  bool[] visited = new bool[v];  // Find first vertex with non-zero degree  int start = -1;  for (int i = 0; i < v; i++) {  if (adj[i].Count > 0) {  start = i;  break;  }  }  // No edges: graph is trivially Eulerian  if (start == -1) {  return 2;  }  // DFS from the first non-zero degree vertex  dfs(start, adj, visited);  // Check if all non-zero degree vertices are connected  for (int i = 0; i < v; i++) {  if (adj[i].Count > 0 && !visited[i]) {  return 0; // Not connected  }  }  // Count vertices with odd degree  int odd = 0;  for (int i = 0; i < v; i++) {  if (adj[i].Count % 2 != 0) {  odd++;  }  }  // Apply Eulerian rules  if (odd == 0) {  return 2;   } else if (odd == 2) {  return 1;   } else {  return 0;   }  }  static void Main() {  int v = 5;  List<int>[] adj = new List<int>[v];  for (int i = 0; i < v; i++) {  adj[i] = new List<int>();  }  adj[0].AddRange(new int[] {1, 2, 3});  adj[1].AddRange(new int[] {0, 2});  adj[2].AddRange(new int[] {1, 0});  adj[3].AddRange(new int[] {0, 4});  adj[4].AddRange(new int[] {3});  Console.WriteLine(isEulerCircuit(v, adj));  } } 

// JavaScript program to check whether a graph is // Eulerian Path, Eulerian Circuit, or neither // DFS to check connectivity, excluding zero-degree vertices function dfs(node, adj, visited) {  visited[node] = true;  for (let neighbor of adj[node]) {  if (!visited[neighbor]) {  dfs(neighbor, adj, visited);  }  } } // Function to check Eulerian Path or Circuit function isEulerCircuit(v, adj) {  let visited = new Array(v).fill(false);  // Find first vertex with non-zero degree  let start = -1;  for (let i = 0; i < v; i++) {  if (adj[i].length > 0) {  start = i;  break;  }  }  // No edges: graph is trivially Eulerian  if (start === -1) {  return 2;  }  // DFS from the first non-zero degree vertex  dfs(start, adj, visited);  // Check if all non-zero degree vertices are connected  for (let i = 0; i < v; i++) {  if (adj[i].length > 0 && !visited[i]) {  return 0; // Not connected  }  }  // Count vertices with odd degree  let odd = 0;  for (let i = 0; i < v; i++) {  if (adj[i].length % 2 !== 0) {  odd++;  }  }  // Apply Eulerian rules  if (odd === 0) {  return 2;   } else if (odd === 2) {  return 1;   } else {  return 0;   } } // Driver Code let v = 5; let adj = [  [1, 2, 3],   [0, 2],   [1, 0],   [0, 4],   [3] ]; console.log(isEulerCircuit(v, adj)); 

1

Time Complexity: O(v + e), DFS traverses all vertices and edges to check connectivity and degree.
Space Complexity: O(v + e), Space used for visited array and adjacency list to represent graph.