Detect Cycle in a Directed Graph using BFS

Last Updated : 28 Jul, 2022

Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false. For example, the following graph contains two cycles 0->1->2->3->0 and 2->4->2, so your function must return true.

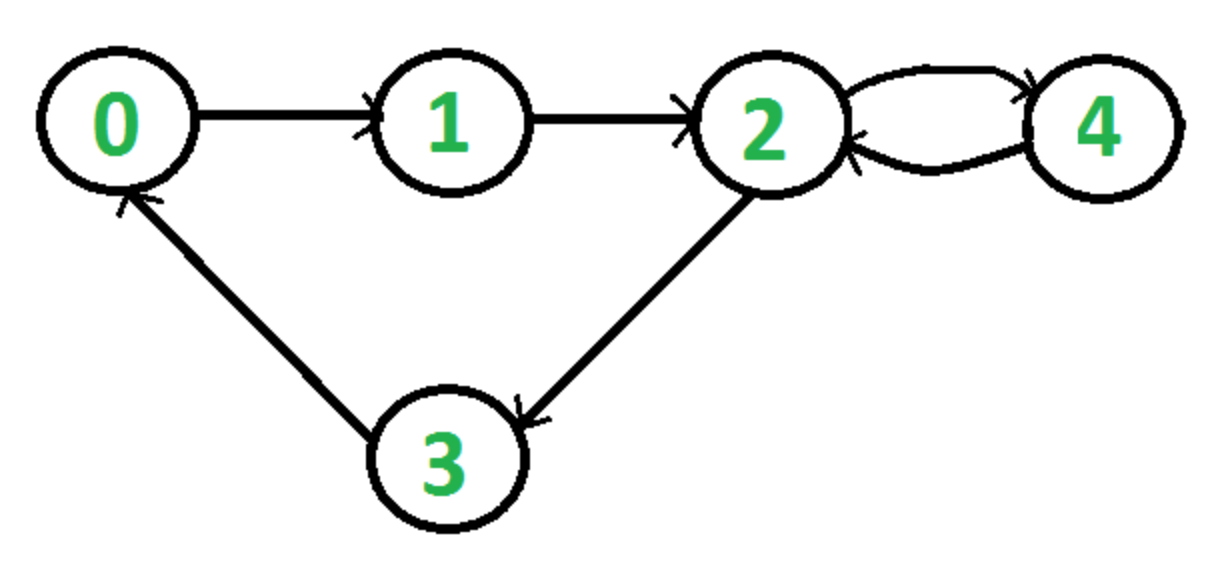
We have discussed a DFS based solution to detect cycle in a directed graph. In this post, BFS based solution is discussed.
The idea is to simply use Kahn's algorithm for Topological Sorting

Steps involved in detecting cycle in a directed graph using BFS.
Step-1: Compute in-degree (number of incoming edges) for each of the vertex present in the graph and initialize the count of visited nodes as 0.
Step-2: Pick all the vertices with in-degree as 0 and add them into a queue (Enqueue operation)
Step-3: Remove a vertex from the queue (Dequeue operation) and then.

Increment count of visited nodes by 1.
Decrease in-degree by 1 for all its neighboring nodes.
If in-degree of a neighboring nodes is reduced to zero, then add it to the queue.

Step 4: Repeat Step 3 until the queue is empty.
Step 5: If count of visited nodes is not equal to the number of nodes in the graph has cycle, otherwise not.

How to find in-degree of each node?
There are 2 ways to calculate in-degree of every vertex:
Take an in-degree array which will keep track of
1) Traverse the array of edges and simply increase the counter of the destination node by 1.

for each node in Nodes indegree[node] = 0; for each edge(src,dest) in Edges indegree[dest]++

Time Complexity: O(V+E)

2) Traverse the list for every node and then increment the in-degree of all the nodes connected to it by 1.

 for each node in Nodes If (list[node].size()!=0) then for each dest in list indegree[dest]++;

Time Complexity: The outer for loop will be executed V number of times and the inner for loop will be executed E number of times, Thus overall time complexity is O(V+E).

The overall time complexity of the algorithm is O(V+E)

C++

// A C++ program to check if there is a cycle in  // directed graph using BFS. #include <bits/stdc++.h> using namespace std; // Class to represent a graph class Graph {  int V; // No. of vertices'  // Pointer to an array containing adjacency list  list<int>* adj; public:  Graph(int V); // Constructor  // function to add an edge to graph  void addEdge(int u, int v);  // Returns true if there is a cycle in the graph  // else false.  bool isCycle(); }; Graph::Graph(int V) {  this->V = V;  adj = new list<int>[V]; } void Graph::addEdge(int u, int v) {  adj[u].push_back(v); } // This function returns true if there is a cycle // in directed graph, else returns false. bool Graph::isCycle() {  // Create a vector to store indegrees of all  // vertices. Initialize all indegrees as 0.  vector<int> in_degree(V, 0);  // Traverse adjacency lists to fill indegrees of  // vertices. This step takes O(V+E) time  for (int u = 0; u < V; u++) {  for (auto v : adj[u])  in_degree[v]++;  }  // Create an queue and enqueue all vertices with  // indegree 0  queue<int> q;  for (int i = 0; i < V; i++)  if (in_degree[i] == 0)  q.push(i);  // Initialize count of visited vertices  // 1 For src Node   int cnt = 1;  // Create a vector to store result (A topological  // ordering of the vertices)  vector<int> top_order;  // One by one dequeue vertices from queue and enqueue  // adjacents if indegree of adjacent becomes 0  while (!q.empty()) {  // Extract front of queue (or perform dequeue)  // and add it to topological order  int u = q.front();  q.pop();  top_order.push_back(u);  // Iterate through all its neighbouring nodes  // of dequeued node u and decrease their in-degree  // by 1  list<int>::iterator itr;  for (itr = adj[u].begin(); itr != adj[u].end(); itr++)  // If in-degree becomes zero, add it to queue  if (--in_degree[*itr] == 0)  {  q.push(*itr);  //while we are pushing elements to the queue we will incrementing the cnt  cnt++;  }     }  // Check if there was a cycle  if (cnt != V)   return true;  else  return false; } // Driver program to test above functions int main() {  // Create a graph given in the above diagram  Graph g(6);  g.addEdge(0, 1);  g.addEdge(1, 2);  g.addEdge(2, 0);  g.addEdge(3, 4);  g.addEdge(4, 5);  if (g.isCycle())  cout << "Yes";  else  cout << "No";  return 0; }

Java

// Java program to check if there is a cycle in  // directed graph using BFS. import java.io.*; import java.util.*; class GFG {  // Class to represent a graph  static class Graph  {  int V; // No. of vertices'  // Pointer to an array containing adjacency list  Vector<Integer>[] adj;  @SuppressWarnings("unchecked")  Graph(int V)  {  // Constructor  this.V = V;  this.adj = new Vector[V];  for (int i = 0; i < V; i++)  adj[i] = new Vector<>();  }  // function to add an edge to graph  void addEdge(int u, int v)  {  adj[u].add(v);  }  // Returns true if there is a cycle in the graph  // else false.  // This function returns true if there is a cycle  // in directed graph, else returns false.  boolean isCycle()   {  // Create a vector to store indegrees of all  // vertices. Initialize all indegrees as 0.  int[] in_degree = new int[this.V];  Arrays.fill(in_degree, 0);  // Traverse adjacency lists to fill indegrees of  // vertices. This step takes O(V+E) time  for (int u = 0; u < V; u++)  {  for (int v : adj[u])  in_degree[v]++;  }  // Create an queue and enqueue all vertices with  // indegree 0  Queue<Integer> q = new LinkedList<Integer>();  for (int i = 0; i < V; i++)  if (in_degree[i] == 0)  q.add(i);  // Initialize count of visited vertices  int cnt = 0;  // Create a vector to store result (A topological  // ordering of the vertices)  Vector<Integer> top_order = new Vector<>();  // One by one dequeue vertices from queue and enqueue  // adjacents if indegree of adjacent becomes 0  while (!q.isEmpty())  {  // Extract front of queue (or perform dequeue)  // and add it to topological order  int u = q.poll();  top_order.add(u);  // Iterate through all its neighbouring nodes  // of dequeued node u and decrease their in-degree  // by 1  for (int itr : adj[u])  if (--in_degree[itr] == 0)  q.add(itr);  cnt++;  }  // Check if there was a cycle  if (cnt != this.V)  return true;  else  return false;  }  }  // Driver Code  public static void main(String[] args)   {  // Create a graph given in the above diagram  Graph g = new Graph(6);  g.addEdge(0, 1);  g.addEdge(1, 2);  g.addEdge(2, 0);  g.addEdge(3, 4);  g.addEdge(4, 5);  if (g.isCycle())  System.out.println("Yes");  else  System.out.println("No");  } } // This code is contributed by // sanjeev2552

Python3

# A Python3 program to check if there is a cycle in  # directed graph using BFS.  import math import sys from collections import defaultdict # Class to represent a graph  class Graph: def __init__(self,vertices): self.graph=defaultdict(list) self.V=vertices # No. of vertices'  # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # This function returns true if there is a cycle  # in directed graph, else returns false.  def isCycleExist(n,graph): # Create a vector to store indegrees of all  # vertices. Initialize all indegrees as 0.  in_degree=[0]*n # Traverse adjacency lists to fill indegrees of  # vertices. This step takes O(V+E) time for i in range(n): for j in graph[i]: in_degree[j]+=1 # Create an queue and enqueue all vertices with  # indegree 0 queue=[] for i in range(len(in_degree)): if in_degree[i]==0: queue.append(i) # Initialize count of visited vertices cnt=0 # One by one dequeue vertices from queue and enqueue  # adjacents if indegree of adjacent becomes 0  while(queue): # Extract front of queue (or perform dequeue)  # and add it to topological order  nu=queue.pop(0) # Iterate through all its neighbouring nodes  # of dequeued node u and decrease their in-degree  # by 1  for v in graph[nu]: in_degree[v]-=1 # If in-degree becomes zero, add it to queue if in_degree[v]==0: queue.append(v) cnt+=1 # Check if there was a cycle  if cnt==n: return False else: return True # Driver program to test above functions  if __name__=='__main__': # Create a graph given in the above diagram g=Graph(6) g.addEdge(0,1) g.addEdge(1,2) g.addEdge(2,0) g.addEdge(3,4) g.addEdge(4,5) if isCycleExist(g.V,g.graph): print("Yes") else: print("No") # This Code is Contributed by Vikash Kumar 37

// C# program to check if there is a cycle in  // directed graph using BFS. using System; using System.Collections.Generic; class GFG{   // Class to represent a graph public class Graph {    // No. of vertices'  public int V;     // Pointer to an array containing  // adjacency list  public List<int>[] adj;    public Graph(int V)  {    // Constructor  this.V = V;  this.adj = new List<int>[V];  for (int i = 0; i < V; i++)  adj[i] = new List<int>();  }    // Function to add an edge to graph  public void addEdge(int u, int v)  {  adj[u].Add(v);  }    // Returns true if there is a cycle in the  // graph else false.    // This function returns true if there is   // a cycle in directed graph, else returns  // false.  public bool isCycle()   {    // Create a vector to store indegrees of all  // vertices. Initialize all indegrees as 0.  int[] in_degree = new int[this.V];    // Traverse adjacency lists to fill indegrees  // of vertices. This step takes O(V+E) time  for(int u = 0; u < V; u++)  {  foreach(int v in adj[u])  in_degree[v]++;  }    // Create an queue and enqueue all   // vertices with indegree 0  Queue<int> q = new Queue<int>();  for(int i = 0; i < V; i++)  if (in_degree[i] == 0)  q.Enqueue(i);    // Initialize count of visited vertices  int cnt = 0;    // Create a vector to store result   // (A topological ordering of the   // vertices)  List<int> top_order = new List<int>();    // One by one dequeue vertices from   // queue and enqueue adjacents if  // indegree of adjacent becomes 0  while (q.Count != 0)  {    // Extract front of queue (or perform   // dequeue) and add it to topological  // order  int u = q.Peek();  q.Dequeue();  top_order.Add(u);    // Iterate through all its neighbouring   // nodes of dequeued node u and decrease  // their in-degree by 1  foreach(int itr in adj[u])  if (--in_degree[itr] == 0)  q.Enqueue(itr);    cnt++;  }    // Check if there was a cycle  if (cnt != this.V)  return true;  else  return false;  } } // Driver Code public static void Main(String[] args)  {    // Create a graph given in the above diagram  Graph g = new Graph(6);  g.addEdge(0, 1);  g.addEdge(1, 2);  g.addEdge(2, 0);  g.addEdge(3, 4);  g.addEdge(4, 5);  if (g.isCycle())  Console.WriteLine("Yes");  else  Console.WriteLine("No"); } } // This code is contributed by Princi Singh

JavaScript

<script> // JavaScript program to check if there is a cycle in  // directed graph using BFS. // Class to represent a graph // No. of vertices' var V = 0;  // Pointer to an array containing // adjacency list var adj ; function initialize(v) {    // Constructor  V = v;  adj = Array.from(Array(V), ()=>Array(V)); } // Function to add an edge to graph function addEdge(u, v) {  adj[u].push(v); } // Returns true if there is a cycle in the // graph else false. // This function returns true if there is  // a cycle in directed graph, else returns // false. function isCycle()  {    // Create a vector to store indegrees of all  // vertices. Initialize all indegrees as 0.  var in_degree = Array(V).fill(0);    // Traverse adjacency lists to fill indegrees  // of vertices. This step takes O(V+E) time  for(var u = 0; u < V; u++)  {  for(var v of adj[u])  in_degree[v]++;  }    // Create an queue and enqueue all   // vertices with indegree 0  var q = [];  for(var i = 0; i < V; i++)  if (in_degree[i] == 0)  q.push(i);    // Initialize count of visited vertices  var cnt = 0;    // Create a vector to store result   // (A topological ordering of the   // vertices)  var top_order = [];    // One by one dequeue vertices from   // queue and enqueue adjacents if  // indegree of adjacent becomes 0  while (q.length != 0)  {    // Extract front of queue (or perform   // dequeue) and add it to topological  // order  var u = q[0];  q.shift();  top_order.push(u);    // Iterate through all its neighbouring   // nodes of dequeued node u and decrease  // their in-degree by 1  for(var itr of adj[u])  if (--in_degree[itr] == 0)  q.push(itr);    cnt++;  }    // Check if there was a cycle  if (cnt != V)  return true;  else  return false; } // Create a graph given in the above diagram initialize(6) addEdge(0, 1); addEdge(1, 2); addEdge(2, 0); addEdge(3, 4); addEdge(4, 5); if (isCycle())  document.write("Yes"); else  document.write("No"); </script>