Convert Binary Tree to Doubly Linked List using inorder traversal
Last Updated : 23 Jul, 2025
Given a Binary Tree (BT), the task is to convert it to a Doubly Linked List (DLL) in place. The left and right pointers in nodes will be used as previous and next pointers respectively in converted DLL. The order of nodes in DLL must be the same as the order of the given Binary Tree. The first node of Inorder traversal (leftmost node in BT) must be the head node of the DLL.
Examples:
Input:
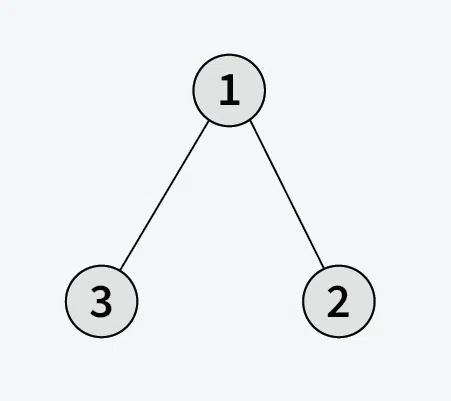
Output:

Explanation: The above binary tree is converted into doubly linked list where left pointer of the binary tree node act as the previous node and right pointer of the binary tree node act as the next node.
Input:
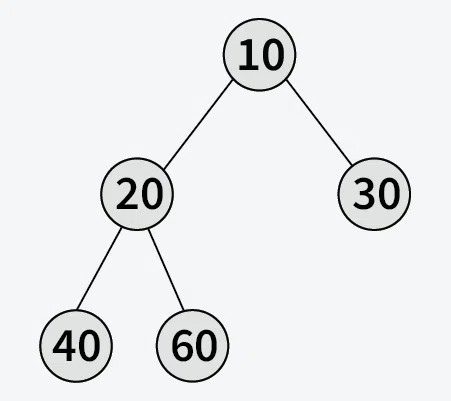
Output:

Explanation: The above binary tree is converted into doubly linked list where left pointer of the binary tree node act as the previous node and right pointer of the binary tree node act as the next node.
[Naive Approach] Using Recursion - O(n) Time and O(h) Space
The idea is to recursively traverse the binary tree using inorder traversal. At each node, if left subtree exists, find theinorder predecessor, then process the left subtree and link the current node and predecessor. If right subtree exists, then find theinorder successor, process the right subtree and then link the current node and successor node.
Below is the implementation of the above approach:
C++ // C++ program for in-place // conversion of Binary Tree to DLL #include <bits/stdc++.h> using namespace std; class Node { public: int data; Node* left; Node* right; Node (int x) { data = x; left = nullptr; right = nullptr; } }; void inorder(Node* root) { // if left subtree exists if (root->left){ // find the inorder predecessor of root node Node* pred = root->left; while (pred->right){ pred = pred->right; } // process the left subtree inorder(root->left); // link the predecessor and root node pred->right = root; root->left = pred; } // if right subtree exists if (root->right) { // find the inorder successor of root node Node* succ = root->right; while (succ->left) { succ = succ->left; } // process the right subtree inorder(root->right); // link the successor and root node root->right = succ; succ->left = root; } } Node* bToDLL(Node* root){ // return if root is null if (root == nullptr) return root; // find the head of dll Node* head = root; while (head->left != nullptr) head = head->left; // recursively convert the tree into dll inorder(root); return head; } void printList(Node* head){ Node* curr = head; while (curr != NULL) { cout << curr->data << " "; curr = curr->right; } cout<<endl; } int main() { // Create a hard coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 Node* root = new Node(10); root->left = new Node(12); root->right = new Node(15); root->left->left = new Node(25); root->left->right = new Node(30); root->right->left = new Node(36); Node* head = bToDLL(root); printList(head); return 0; } // C program for in-place // conversion of Binary Tree to DLL #include <stdio.h> #include <stdlib.h> struct Node { int data; struct Node* left; struct Node* right; }; // Inorder traversal to link nodes void inorder(struct Node* root) { // if left subtree exists if (root->left) { // find the inorder predecessor of root node struct Node* pred = root->left; while (pred->right) { pred = pred->right; } // process the left subtree inorder(root->left); // link the predecessor and root node pred->right = root; root->left = pred; } // if right subtree exists if (root->right) { // find the inorder successor of root node struct Node* succ = root->right; while (succ->left) { succ = succ->left; } // process the right subtree inorder(root->right); // link the successor and root node root->right = succ; succ->left = root; } } // Function to convert binary tree to doubly linked list struct Node* bToDLL(struct Node* root) { // return if root is null if (root == NULL) return root; // find the head of dll struct Node* head = root; while (head->left != NULL) head = head->left; // recursively convert the tree into dll inorder(root); return head; } void printList(struct Node* head) { struct Node* curr = head; while (curr != NULL) { printf("%d ", curr->data); curr = curr->right; } printf("\n"); } struct Node* createNode(int x) { struct Node* node = (struct Node*)malloc(sizeof(struct Node)); node->data = x; node->left = NULL; node->right = NULL; return node; } int main() { // Create a hard coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 struct Node* root = createNode(10); root->left = createNode(12); root->right = createNode(15); root->left->left = createNode(25); root->left->right = createNode(30); root->right->left = createNode(36); struct Node* head = bToDLL(root); printList(head); return 0; } // Java program for in-place // conversion of Binary Tree to DLL class Node { int data; Node left, right; Node(int x) { data = x; left = null; right = null; } } class GfG { // Inorder traversal to link nodes static void inorder(Node root) { // if left subtree exists if (root.left != null) { // find the inorder predecessor of root node Node pred = root.left; while (pred.right != null) { pred = pred.right; } // process the left subtree inorder(root.left); // link the predecessor and root node pred.right = root; root.left = pred; } // if right subtree exists if (root.right != null) { // find the inorder successor of root node Node succ = root.right; while (succ.left != null) { succ = succ.left; } // process the right subtree inorder(root.right); // link the successor and root node root.right = succ; succ.left = root; } } // Function to convert binary tree to doubly linked list static Node bToDLL(Node root) { // return if root is null if (root == null) return root; // find the head of dll Node head = root; while (head.left != null) head = head.left; // recursively convert the tree into dll inorder(root); return head; } static void printList(Node head) { Node curr = head; while (curr != null) { System.out.print(curr.data + " "); curr = curr.right; } System.out.println(); } public static void main(String[] args) { // Create a hard coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 Node root = new Node(10); root.left = new Node(12); root.right = new Node(15); root.left.left = new Node(25); root.left.right = new Node(30); root.right.left = new Node(36); Node head = bToDLL(root); printList(head); } } # Python program for in-place # conversion of Binary Tree to DLL class Node: def __init__(self, new_value): self.data = new_value self.left = None self.right = None # Inorder traversal to link nodes def inorder(root): # if left subtree exists if root.left: # find the inorder predecessor of root node pred = root.left while pred.right: pred = pred.right # process the left subtree inorder(root.left) # link the predecessor and root node pred.right = root root.left = pred # if right subtree exists if root.right: # find the inorder successor of root node succ = root.right while succ.left: succ = succ.left # process the right subtree inorder(root.right) # link the successor and root node root.right = succ succ.left = root # Function to convert binary tree to doubly linked list def bToDLL(root): # return if root is null if root is None: return root # find the head of dll head = root while head.left: head = head.left # recursively convert the tree into dll inorder(root) return head def print_list(head): curr = head while curr: print(curr.data, end=" ") curr = curr.right print() if __name__ == "__main__": # Create a hard coded binary tree # 10 # / \ # 12 15 # / \ / # 25 30 36 root = Node(10) root.left = Node(12) root.right = Node(15) root.left.left = Node(25) root.left.right = Node(30) root.right.left = Node(36) head = bToDLL(root) print_list(head)
// C# program for in-place // conversion of Binary Tree to DLL using System; class Node { public int data; public Node left, right; public Node(int x) { data = x; left = right = null; } } class GfG { // Inorder traversal to link nodes static void Inorder(Node root) { // if left subtree exists if (root.left != null) { // find the inorder predecessor of root node Node pred = root.left; while (pred.right != null) { pred = pred.right; } // process the left subtree Inorder(root.left); // link the predecessor and root node pred.right = root; root.left = pred; } // if right subtree exists if (root.right != null) { // find the inorder successor of root node Node succ = root.right; while (succ.left != null) { succ = succ.left; } // process the right subtree Inorder(root.right); // link the successor and root node root.right = succ; succ.left = root; } } // Function to convert binary tree to doubly linked list static Node BToDLL(Node root) { // return if root is null if (root == null) return root; // find the head of dll Node head = root; while (head.left != null) head = head.left; // recursively convert the tree into dll Inorder(root); return head; } static void PrintList(Node head) { Node curr = head; while (curr != null) { Console.Write(curr.data + " "); curr = curr.right; } Console.WriteLine(); } static void Main(string[] args) { // Create a hard coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 Node root = new Node(10); root.left = new Node(12); root.right = new Node(15); root.left.left = new Node(25); root.left.right = new Node(30); root.right.left = new Node(36); Node head = BToDLL(root); PrintList(head); } } // JavaScript program for in-place // conversion of Binary Tree to DLL class Node { constructor(new_value) { this.data = new_value; this.left = null; this.right = null; } } // Inorder traversal to link nodes function inorder(root) { // if left subtree exists if (root.left) { // find the inorder predecessor of root node let pred = root.left; while (pred.right) { pred = pred.right; } // process the left subtree inorder(root.left); // link the predecessor and root node pred.right = root; root.left = pred; } // if right subtree exists if (root.right) { // find the inorder successor of root node let succ = root.right; while (succ.left) { succ = succ.left; } // process the right subtree inorder(root.right); // link the successor and root node root.right = succ; succ.left = root; } } // Function to convert binary tree to doubly linked list function bToDLL(root) { // return if root is null if (root === null) return root; // find the head of dll let head = root; while (head.left !== null) head = head.left; // recursively convert the tree into dll inorder(root); return head; } function printList(head) { let curr = head; while (curr !== null) { console.log(curr.data); curr = curr.right; } } // Create a hard coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 let root = new Node(10); root.left = new Node(12); root.right = new Node(15); root.left.left = new Node(25); root.left.right = new Node(30); root.right.left = new Node(36); let head = bToDLL(root); printList(head); Time Complexity: O(n), where n is the number of node in the tree.
Auxiliary Space: O(h), where h is the height of tree.
[Expected Approach] Using Morris Traversal Algorithm - O(n) Time and O(1) Space
The idea is to use Morris traversal algorithmto traverse the binary tree, while maintaining proper linkages between the nodes.
Step by step implementation:
- Initialize pointers head and tail. head will point to the head node of the resultant dll and tail will point to the last node in dll.
- Initialize another pointer curr, which will initially point to root node. Start traversing until curr is not NULL
- If curr.left is null, then add the current node to the list (If head is empty, then make this node as head node) and move curr to curr.right.
- If curr.left is not null, then find the inorder predecessor of the current node. Let that node be 'pred'. There are two possibilites:
- If pred.right is equal to null, then create a link between pred and curr, by setting pred.right = curr and set curr = curr.left.
- If pred->right is equal to curr, then this means we have traversed the left subtree and now we can add the curr node to the list. Then set curr = curr->right.
- Return the head.
C++ // C++ program for in-place // conversion of Binary Tree to DLL #include <bits/stdc++.h> using namespace std; class Node { public: int data; Node *left; Node *right; Node(int x) { data = x; left = nullptr; right = nullptr; } }; // Function to perform Morris Traversal and convert // binary tree to doubly linked list (DLL) Node* morrisTraversal(Node* root) { // return if root is null if (root == nullptr) return root; // head and tail node for the dll Node* head = nullptr, *tail = nullptr; Node* curr = root; while (curr != nullptr) { // if left tree does not exists, // then add the curr node to the // dll and set curr = curr->right if (curr->left == nullptr) { if (head == nullptr) { head = tail = curr; } else { tail->right = curr; curr->left = tail; tail = curr; } curr = curr->right; } else { Node* pred = curr->left; // find the inorder predecessor while (pred->right != nullptr && pred->right != curr) { pred = pred->right; } // create a linkage between pred and // curr if (pred->right == nullptr) { pred->right = curr; curr = curr->left; } // if pred->right = curr, it means // we have processed the left subtree, // and we can add curr node to list else { tail->right = curr; curr->left = tail; tail = curr; curr = curr->right; } } } return head; } void printList(Node* head) { Node* curr = head; while (curr != nullptr) { cout << curr->data << " "; curr = curr->right; } cout << endl; } int main() { // Create a hard-coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 Node* root = new Node(10); root->left = new Node(12); root->right = new Node(15); root->left->left = new Node(25); root->left->right = new Node(30); root->right->left = new Node(36); Node* head = morrisTraversal(root); printList(head); return 0; } // C program for in-place // conversion of Binary Tree to DLL #include <stdio.h> #include <stdlib.h> struct Node { int data; struct Node* left; struct Node* right; }; struct Node* morrisTraversal(struct Node* root) { // return if root is null if (root == NULL) return root; // head and tail node for the dll struct Node* head = NULL, *tail = NULL; struct Node* curr = root; while (curr != NULL) { // if left tree does not exists, // then add the curr node to the // dll and set curr = curr->right if (curr->left == NULL) { if (head == NULL) { head = tail = curr; } else { tail->right = curr; curr->left = tail; tail = curr; } curr = curr->right; } else { struct Node* pred = curr->left; // find the inorder predecessor while (pred->right != NULL && pred->right != curr) { pred = pred->right; } // create a linkage between pred and // curr if (pred->right == NULL) { pred->right = curr; curr = curr->left; } // if pred->right = curr, it means // we have processed the left subtree, // and we can add curr node to list else { tail->right = curr; curr->left = tail; tail = curr; curr = curr->right; } } } return head; } void printList(struct Node* head) { struct Node* curr = head; while (curr != NULL) { printf("%d ", curr->data); curr = curr->right; } printf("\n"); } struct Node* createNode(int new_value) { struct Node* node = (struct Node*)malloc(sizeof(struct Node)); node->data = new_value; node->left = node->right = NULL; return node; } int main() { // Create a hard coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 struct Node* root = createNode(10); root->left = createNode(12); root->right = createNode(15); root->left->left = createNode(25); root->left->right = createNode(30); root->right->left = createNode(36); struct Node* head = morrisTraversal(root); printList(head); return 0; } // Java program for in-place // conversion of Binary Tree to DLL class Node { int data; Node left, right; Node(int x) { data = x; left = null; right = null; } } class GfG { static Node morrisTraversal(Node root) { // return if root is null if (root == null) return root; // head and tail node for the dll Node head = null, tail = null; Node curr = root; while (curr != null) { // if left tree does not exists, // then add the curr node to the // dll and set curr = curr.right if (curr.left == null) { if (head == null) { head = tail = curr; } else { tail.right = curr; curr.left = tail; tail = curr; } curr = curr.right; } else { Node pred = curr.left; // find the inorder predecessor while (pred.right != null && pred.right != curr) { pred = pred.right; } // create a linkage between pred and // curr if (pred.right == null) { pred.right = curr; curr = curr.left; } // if pred.right = curr, it means // we have processed the left subtree, // and we can add curr node to list else { tail.right = curr; curr.left = tail; tail = curr; curr = curr.right; } } } return head; } static void printList(Node head) { Node curr = head; while (curr != null) { System.out.print(curr.data + " "); curr = curr.right; } System.out.println(); } public static void main(String[] args) { // Create a hard coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 Node root = new Node(10); root.left = new Node(12); root.right = new Node(15); root.left.left = new Node(25); root.left.right = new Node(30); root.right.left = new Node(36); Node head = morrisTraversal(root); printList(head); } } # Python program for in-place # conversion of Binary Tree to DLL class Node: def __init__(self, new_value): self.data = new_value self.left = None self.right = None def morris_traversal(root): # return if root is None if root is None: return root # head and tail node for the dll head = None tail = None curr = root while curr is not None: # if left tree does not exist, # then add the curr node to the # dll and set curr = curr.right if curr.left is None: if head is None: head = tail = curr else: tail.right = curr curr.left = tail tail = curr curr = curr.right else: pred = curr.left # find the inorder predecessor while pred.right is not None \ and pred.right != curr: pred = pred.right # create a linkage between pred and curr if pred.right is None: pred.right = curr curr = curr.left # if pred.right = curr, it means # we have processed the left subtree, # and we can add curr node to list else: tail.right = curr curr.left = tail tail = curr curr = curr.right return head def print_list(head): curr = head while curr is not None: print(curr.data, end=" ") curr = curr.right print() if __name__ == "__main__": # Create a hard coded binary tree # 10 # / \ # 12 15 # / \ / # 25 30 36 root = Node(10) root.left = Node(12) root.right = Node(15) root.left.left = Node(25) root.left.right = Node(30) root.right.left = Node(36) head = morris_traversal(root) print_list(head)
// C# program for in-place // conversion of Binary Tree to DLL using System; class Node { public int data; public Node left, right; public Node(int x) { data = x; left = null; right = null; } } class GfG { static Node MorrisTraversal(Node root) { // return if root is null if (root == null) return root; // head and tail node for the dll Node head = null, tail = null; Node curr = root; while (curr != null) { // if left tree does not exists, // then add the curr node to the // dll and set curr = curr.right if (curr.left == null) { if (head == null) { head = tail = curr; } else { tail.right = curr; curr.left = tail; tail = curr; } curr = curr.right; } else { Node pred = curr.left; // find the inorder predecessor while (pred.right != null && pred.right != curr) { pred = pred.right; } // create a linkage between pred and // curr if (pred.right == null) { pred.right = curr; curr = curr.left; } // if pred.right = curr, it means // we have processed the left subtree, // and we can add curr node to list else { tail.right = curr; curr.left = tail; tail = curr; curr = curr.right; } } } return head; } static void PrintList(Node head) { Node curr = head; while (curr != null) { Console.Write(curr.data + " "); curr = curr.right; } Console.WriteLine(); } static void Main(string[] args) { // Create a hard coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 Node root = new Node(10); root.left = new Node(12); root.right = new Node(15); root.left.left = new Node(25); root.left.right = new Node(30); root.right.left = new Node(36); Node head = MorrisTraversal(root); PrintList(head); } } // JavaScript program for in-place // conversion of Binary Tree to DLL class Node { constructor(new_value) { this.data = new_value; this.left = this.right = null; } } function morrisTraversal(root) { // return if root is null if (root === null) return root; // head and tail node for the dll let head = null, tail = null; let curr = root; while (curr !== null) { // if left tree does not exists, // then add the curr node to the // dll and set curr = curr.right if (curr.left === null) { if (head === null) { head = tail = curr; } else { tail.right = curr; curr.left = tail; tail = curr; } curr = curr.right; } else { let pred = curr.left; // find the inorder predecessor while (pred.right !== null && pred.right !== curr) { pred = pred.right; } // create a linkage between pred and curr if (pred.right === null) { pred.right = curr; curr = curr.left; } // if pred.right = curr, it means // we have processed the left subtree, // and we can add curr node to list else { tail.right = curr; curr.left = tail; tail = curr; curr = curr.right; } } } return head; } function printList(head) { let curr = head; while (curr !== null) { console.log(curr.data); curr = curr.right; } } // Create a hard coded binary tree // 10 // / \ // 12 15 // / \ / // 25 30 36 let root = new Node(10); root.left = new Node(12); root.right = new Node(15); root.left.left = new Node(25); root.left.right = new Node(30); root.right.left = new Node(36); let head = morrisTraversal(root); printList(head); Time Complexity: O(n), where n is the number of nodes in tree.
Auxiliary Space: O(1)
Explore
DSA Fundamentals
Data Structures
Algorithms
Advanced
Interview Preparation
Practice Problem
My Profile