Binary Tree to Binary Search Tree Conversion

Last Updated : 23 Jul, 2025

Given a Binary Tree, the task is to convert it to a Binary Search Tree. The conversion must be done in such a way that keeps the original structure of the Binary Tree.

Examples

Input:

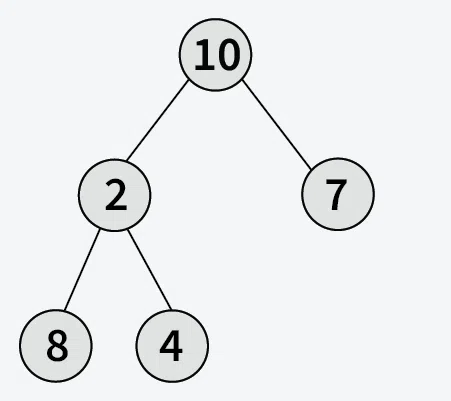
Output:

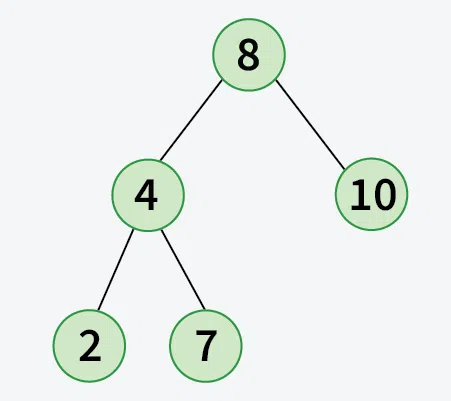
Explanation: The above Binary tree is converted to Binary Search tree by keeping the original structure of Binary Tree.

Approach:

The idea to recursively traverse the binary tree and store the nodes in an array. Sort the array, and perform in-order traversal of the tree and update the value of each node to the corresponding value in tree.

Below is the implementation of the above approach:

C++

// C++ Program to convert binary  // tree to binary search tree. #include <bits/stdc++.h> using namespace std; class Node { public:  int data;  Node* left, *right;  Node(int x) {  data = x;  left = nullptr;  right = nullptr;  } }; // Inorder traversal to store the nodes in a vector void inorder(Node* root, vector<int>& nodes) {  if (root == nullptr) {  return;  }  inorder(root->left, nodes);  nodes.push_back(root->data);  inorder(root->right, nodes); } // Inorder traversal to convert tree // to BST. void constructBST(Node* root, vector<int> nodes, int& index) {  if (root == nullptr) return;    constructBST(root->left, nodes, index);    // Update root value  root->data = nodes[index++];    constructBST(root->right, nodes, index); } // Function to convert a binary tree to a binary search tree Node* binaryTreeToBST(Node* root) {  vector<int> nodes;  inorder(root, nodes);    // sort the nodes  sort(nodes.begin(), nodes.end());    int index = 0;  constructBST(root, nodes, index);  return root; } // Function to print the inorder traversal of a binary tree void printInorder(Node* root) {  if (root == NULL) {  return;  }  printInorder(root->left);  cout << root->data << " ";  printInorder(root->right); } int main() {    // Creating the tree  // 10  // / \  // 2 7  // / \  // 8 4  Node* root = new Node(10);   root->left = new Node(2);   root->right = new Node(7);   root->left->left = new Node(8);   root->left->right = new Node(4);    Node* ans = binaryTreeToBST(root);  printInorder(ans);  return 0; }

Java

// Java Program to convert binary  // tree to binary search tree. import java.util.ArrayList; import java.util.Collections; class Node {  int data;  Node left, right;  Node(int x) {  data = x;  left = null;  right = null;  } } class GfG {    // Inorder traversal to store the nodes in a vector  static void inorder(Node root, ArrayList<Integer> nodes) {  if (root == null) {  return;  }  inorder(root.left, nodes);  nodes.add(root.data);  inorder(root.right, nodes);  }  // Inorder traversal to convert tree to BST.  static void constructBST(Node root,   ArrayList<Integer> nodes, int[] index) {  if (root == null) return;  constructBST(root.left, nodes, index);  // Update root value  root.data = nodes.get(index[0]);  index[0]++;  constructBST(root.right, nodes, index);  }  // Function to convert a binary tree to a binary search tree  static Node binaryTreeToBST(Node root) {  ArrayList<Integer> nodes = new ArrayList<>();  inorder(root, nodes);  // sort the nodes  Collections.sort(nodes);  int[] index = {0};  constructBST(root, nodes, index);  return root;  }  // Function to print the inorder traversal of a binary tree  static void printInorder(Node root) {  if (root == null) {  return;  }  printInorder(root.left);  System.out.print(root.data + " ");  printInorder(root.right);  }  public static void main(String[] args) {    // Creating the tree  // 10  // / \  // 2 7  // / \  // 8 4  Node root = new Node(10);  root.left = new Node(2);  root.right = new Node(7);  root.left.left = new Node(8);  root.left.right = new Node(4);  Node ans = binaryTreeToBST(root);  printInorder(ans);  } }

Python

# Python Program to convert binary  # tree to binary search tree. class Node: def __init__(self, x): self.data = x self.left = None self.right = None # Inorder traversal to store the nodes in a vector def inorder(root, nodes): if root is None: return inorder(root.left, nodes) nodes.append(root.data) inorder(root.right, nodes) # Inorder traversal to convert tree to BST. def constructBst(root, nodes, index): if root is None: return constructBst(root.left, nodes, index) # Update root value root.data = nodes[index[0]] index[0] += 1 constructBst(root.right, nodes, index) # Function to convert a binary tree to a binary search tree def binaryTreeToBst(root): nodes = [] inorder(root, nodes) # sort the nodes nodes.sort() index = [0] constructBst(root, nodes, index) return root # Function to print the inorder traversal of a binary tree def printInorder(root): if root is None: return printInorder(root.left) print(root.data, end=" ") printInorder(root.right) if __name__ == "__main__": # Creating the tree # 10 # / \ # 2 7 # / \ # 8 4 root = Node(10) root.left = Node(2) root.right = Node(7) root.left.left = Node(8) root.left.right = Node(4) ans = binaryTreeToBst(root) printInorder(ans)

// C# Program to convert binary  // tree to binary search tree. using System; using System.Collections.Generic; class Node {  public int data;  public Node left, right;  public Node(int x) {  data = x;  left = null;  right = null;  } } class GfG {    // Inorder traversal to store the nodes in a list  static void Inorder(Node root, List<int> nodes) {  if (root == null) {  return;  }  Inorder(root.left, nodes);  nodes.Add(root.data);  Inorder(root.right, nodes);  }  // Inorder traversal to convert tree to BST.  static void ConstructBST(Node root,   List<int> nodes, ref int index) {  if (root == null) return;  ConstructBST(root.left, nodes, ref index);  // Update root value  root.data = nodes[index];  index++;  ConstructBST(root.right, nodes, ref index);  }  // Function to convert a binary tree to a binary search tree  static Node BinaryTreeToBST(Node root) {  List<int> nodes = new List<int>();  Inorder(root, nodes);  // sort the nodes  nodes.Sort();  int index = 0;  ConstructBST(root, nodes, ref index);  return root;  }  // Function to print the inorder traversal of a binary tree  static void PrintInorder(Node root) {  if (root == null) {  return;  }  PrintInorder(root.left);  Console.Write(root.data + " ");  PrintInorder(root.right);  }  static void Main() {    // Creating the tree  // 10  // / \  // 2 7  // / \  // 8 4  Node root = new Node(10);  root.left = new Node(2);  root.right = new Node(7);  root.left.left = new Node(8);  root.left.right = new Node(4);  Node ans = BinaryTreeToBST(root);  PrintInorder(ans);  } }

JavaScript

// JavaScript Program to convert binary  // tree to binary search tree. class Node {  constructor(x) {  this.data = x;  this.left = null;  this.right = null;  } } // Inorder traversal to store the nodes in a vector function inorderTrav(root, nodes) {  if (root === null) {  return;  }  inorderTrav(root.left, nodes);  nodes.push(root.data);  inorderTrav(root.right, nodes); } // Inorder traversal to convert tree to BST. function constructBST(root, nodes, index) {  if (root === null) return;  constructBST(root.left, nodes, index);  // Update root value  root.data = nodes[index[0]];  index[0]++;  constructBST(root.right, nodes, index); } // Function to convert a binary tree to a binary search tree function binaryTreeToBST(root) {  let nodes = [];  inorderTrav(root, nodes);  // sort the nodes  nodes.sort((a, b) => a - b);  let index = [0];  constructBST(root, nodes, index);  return root; } // Function to print the inorder traversal of a binary tree function printInorder(root) {  if (root === null) {  return;  }  printInorder(root.left);  console.log(root.data);  printInorder(root.right); } // Creating the tree // 10 // / \ // 2 7 // / \ // 8 4 let root = new Node(10); root.left = new Node(2); root.right = new Node(7); root.left.left = new Node(8); root.left.right = new Node(4); let ans = binaryTreeToBST(root); printInorder(ans);