Binary Tree to Binary Search Tree Conversion using STL set

Last Updated : 11 Jul, 2025

Given a Binary Tree, the task is to convert it to a Binary Search Tree. The conversion must be done in such a way that keeps the original structure of the Binary Tree.

Example:

Input:
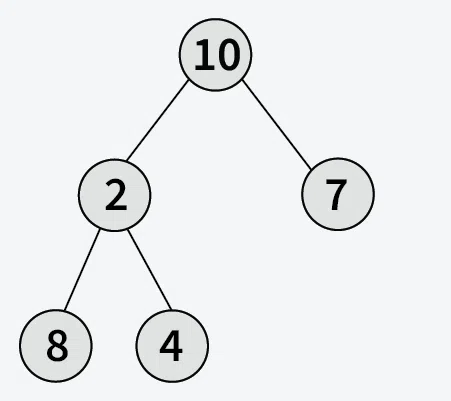
Output:

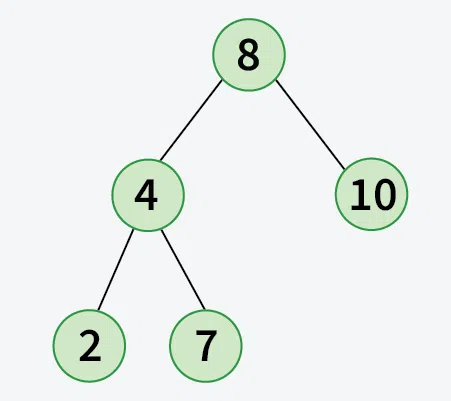
Explanation: The above Binary tree is converted to Binary Search tree by keeping the original structure of Binary Tree.

Approach:

The idea is to recursively traverse the binary tree and insert the value of nodes into a hash set. Then, traverse the tree in in-order manner and pop the smallest value from set and update the value of node to the popped value.
Copy the items of binary tree in a set while doing inorder traversal. This takes O(n log n) time. Note that set in C++ STL is implemented using a Self Balancing Binary Search Tree like Red Black Tree, AVL Tree, etc
There is no need to sort the set as sets in C++ are implemented using Self-balancing binary search trees due to which each operation such as insertion, searching, deletion, etc takes O(log n) time.
Now simply copy the items of set one by one from beginning to the tree while doing inorder traversal of the tree. Care should be taken as when copying each item of set from its beginning, we first copy it to the tree while doing inorder traversal, then remove it from the set as well.

Below is the implementation of the above approach:

C++

// C++ Program to convert binary  // tree to binary search tree. #include <bits/stdc++.h> using namespace std; class Node { public:  int data;  Node* left, *right;  Node(int x) {  data = x;  left = nullptr;  right = nullptr;  } }; // Inorder traversal to store the nodes in a set void inorder(Node* root, set<int>& nodes) {  if (root == nullptr) {  return;  }  inorder(root->left, nodes);  nodes.insert(root->data);  inorder(root->right, nodes); } // Inorder traversal to convert tree // to BST. void constructBST(Node* root, set<int> &nodes) {  if (root == nullptr) return;    constructBST(root->left, nodes);    // Update root value  int val = *nodes.begin();  nodes.erase(nodes.begin());  root->data = val;    constructBST(root->right, nodes); } // Function to convert a binary tree to a  // binary search tree Node* binaryTreeToBST(Node* root) {  set<int> nodes;  inorder(root, nodes);    constructBST(root, nodes);  return root; } // Function to print the inorder traversal // of a binary tree void printInorder(Node* root) {  if (root == nullptr) {  return;  }  printInorder(root->left);  cout << root->data << " ";  printInorder(root->right); } int main() {    // Creating the tree  // 10  // / \  // 2 7  // / \  // 8 4  Node* root = new Node(10);   root->left = new Node(2);   root->right = new Node(7);   root->left->left = new Node(8);   root->left->right = new Node(4);    Node* ans = binaryTreeToBST(root);  printInorder(ans);  return 0; }

Java

// Java Program to convert binary  // tree to binary search tree. import java.util.ArrayList; import java.util.TreeSet; class Node {  int data;  Node left, right;  Node(int x) {  data = x;  left = null;  right = null;  } } class GfG {  // Inorder traversal to store the nodes in a set  static void inorder(Node root, TreeSet<Integer> nodes) {  if (root == null) {  return;  }  inorder(root.left, nodes);  nodes.add(root.data);  inorder(root.right, nodes);  }  // Inorder traversal to convert tree to BST.  static void constructBST(Node root, TreeSet<Integer> nodes) {  if (root == null) return;  constructBST(root.left, nodes);  // Update root value  int val = nodes.first();  nodes.remove(val);  root.data = val;  constructBST(root.right, nodes);  }  // Function to convert a binary tree to a binary search tree  static Node binaryTreeToBST(Node root) {  TreeSet<Integer> nodes = new TreeSet<>();  inorder(root, nodes);  constructBST(root, nodes);  return root;  }  // Function to print the inorder traversal of a binary tree  static void printInorder(Node root) {  if (root == null) {  return;  }  printInorder(root.left);  System.out.print(root.data + " ");  printInorder(root.right);  }  public static void main(String[] args) {    // Creating the tree  // 10  // / \  // 2 7  // / \  // 8 4  Node root = new Node(10);  root.left = new Node(2);  root.right = new Node(7);  root.left.left = new Node(8);  root.left.right = new Node(4);  Node ans = binaryTreeToBST(root);  printInorder(ans);  } }

Python

# Python Program to convert binary  # tree to binary search tree. class Node: def __init__(self, x): self.data = x self.left = None self.right = None # Inorder traversal to store the nodes in a set def inorder(root, nodes): if root is None: return inorder(root.left, nodes) nodes.add(root.data) inorder(root.right, nodes) # Inorder traversal to convert tree to BST. def constructBst(root, nodes): if root is None: return constructBst(root.left, nodes) # Update root value val = min(nodes) nodes.remove(val) root.data = val constructBst(root.right, nodes) # Function to convert a binary tree to a  # binary search tree def binaryTreeToBst(root): nodes = set() inorder(root, nodes) constructBst(root, nodes) return root # Function to print the inorder traversal of  # a binary tree def printInorder(root): if root is None: return printInorder(root.left) print(root.data, end=" ") printInorder(root.right) if __name__ == "__main__": # Creating the tree # 10 # / \ # 2 7 # / \ # 8 4 root = Node(10) root.left = Node(2) root.right = Node(7) root.left.left = Node(8) root.left.right = Node(4) ans = binaryTreeToBst(root) printInorder(ans)

// C# Program to convert binary  // tree to binary search tree. using System; using System.Collections.Generic; class Node {  public int data;  public Node left, right;  public Node(int x) {  data = x;  left = null;  right = null;  } } class GfG {  // Inorder traversal to store the nodes in a set  static void Inorder(Node root, SortedSet<int> nodes) {  if (root == null) {  return;  }  Inorder(root.left, nodes);  nodes.Add(root.data);  Inorder(root.right, nodes);  }  // Inorder traversal to convert tree to BST.  static void ConstructBST(Node root, SortedSet<int> nodes) {  if (root == null) return;  ConstructBST(root.left, nodes);  // Update root value  int val = nodes.Min;  nodes.Remove(val);  root.data = val;  ConstructBST(root.right, nodes);  }  // Function to convert a binary tree to a  // binary search tree  static Node BinaryTreeToBST(Node root) {  SortedSet<int> nodes = new SortedSet<int>();  Inorder(root, nodes);  ConstructBST(root, nodes);  return root;  }  // Function to print the inorder traversal of  // a binary tree  static void PrintInorder(Node root) {  if (root == null) {  return;  }  PrintInorder(root.left);  Console.Write(root.data + " ");  PrintInorder(root.right);  }  static void Main(string[] args) {    // Creating the tree  // 10  // / \  // 2 7  // / \  // 8 4  Node root = new Node(10);  root.left = new Node(2);  root.right = new Node(7);  root.left.left = new Node(8);  root.left.right = new Node(4);  Node ans = BinaryTreeToBST(root);  PrintInorder(ans);  } }

JavaScript

// JavaScript Program to convert binary  // tree to binary search tree. class Node {  constructor(x) {  this.data = x;  this.left = null;  this.right = null;  } } // Inorder traversal to store the nodes in a set function inorderTrav(root, nodes) {  if (root === null) {  return;  }  inorderTrav(root.left, nodes);  nodes.add(root.data);  inorderTrav(root.right, nodes); } // Inorder traversal to convert tree to BST. function constructBST(root, nodes) {  if (root === null) return;  constructBST(root.left, nodes);  // Update root value  const val = Math.min(...nodes);  nodes.delete(val);  root.data = val;  constructBST(root.right, nodes); } // Function to convert a binary tree to a  // binary search tree function binaryTreeToBST(root) {  let nodes = new Set();  inorderTrav(root, nodes);  constructBST(root, nodes);  return root; } // Function to print the inorder traversal of  // a binary tree function printInorder(root) {  if (root === null) {  return;  }  printInorder(root.left);  console.log(root.data);  printInorder(root.right); } // Creating the tree // 10 // / \ // 2 7 // / \ // 8 4 let root = new Node(10); root.left = new Node(2); root.right = new Node(7); root.left.left = new Node(8); root.left.right = new Node(4); let ans = binaryTreeToBST(root); printInorder(ans);