Error Detection Codes - Parity Bit
Last Updated : 07 Oct, 2025
An error detection code is a method used to detect errors during data transmission or storage of digital data.
- Extra bits are added to the original data.
- These bits allow the receiver to detect inconsistencies, indicating potential data errors
Parity Bit Method
A parity bit is an extra bit that is added to the message bits or data-word bits on the sender side. Data-word bits, along with parity bits, are called a codeword. The parity bit is added to the message bits on the sender side to help in error detection at the receiver side. The binary message ensures an odd or even total of 1’s. The parity word counts 1’s in the string.
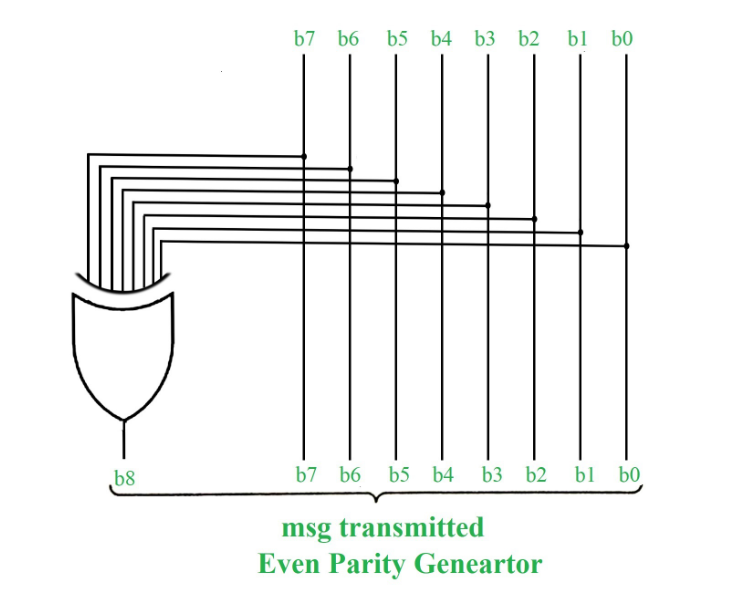
Even Parity
The total number of 1's in the given data bit should be even. So if the total number of 1's in the data bit is odd, then a single 1 will be appended to make the total number of 1's even; else 0 will be appended(if the total number of 1's is already even). Hence, if any error occurs, the parity check circuit will detect it at the receiver's end.

In the above image, as we can see the data bits are '1011000' and since this is even parity check that we're talking about, 1 will be appended as the parity bit (highlighted in red) to make total count of 1's even in the data sent. So here, our parity bit is 1. If the total count of 1 in the given data bits were already even, then 0 would've been appended.
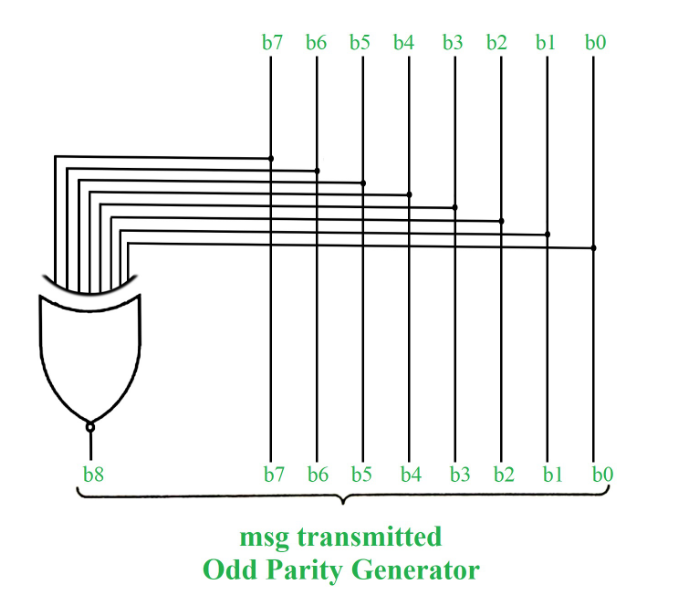
Odd Parity
In odd parity system, if the total number of 1's in the given binary string (or data bits) are even then 1 is appended to make the total count of 1's as odd else 0 is appended. The receiver knows that whether sender is an odd parity generator or even parity generator.
Suppose if sender is an odd parity generator then there must be an odd number of 1’s in received binary string. If an error occurs to a single bit that is either bit is changed to 1 to 0 or 0 to 1, then received binary bit will have an even number of 1’s which will indicate an error.
Take reference from above figure, for odd parity check, rather appending 1 as parity bit, append 0 because total number of 1's are already odd.
Example:
| Message (XYZ) | P(Odd) | P(Even) |
|---|
| 000 | 1 | 0 |
|---|
| 001 | 0 | 1 |
|---|
| 010 | 0 | 1 |
|---|
| 011 | 1 | 0 |
|---|
| 100 | 0 | 1 |
|---|
| 101 | 1 | 0 |
|---|
| 110 | 1 | 0 |
|---|
| 111 | 0 | 1 |
|---|
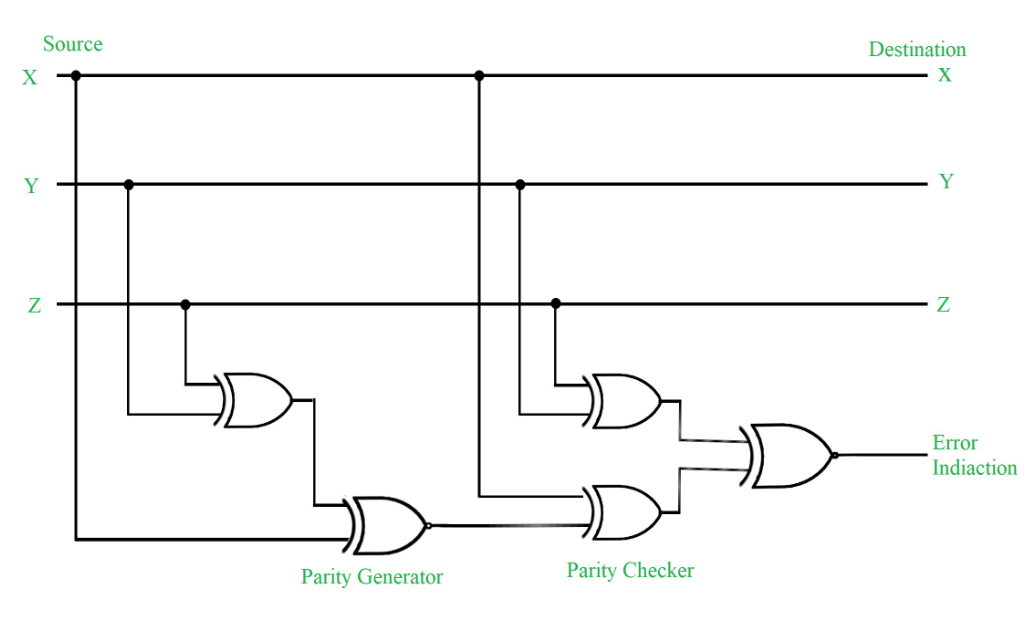 Figure - Error Detection with Odd Parity Bit
Figure - Error Detection with Odd Parity Bit
What if more than 1 bit changed?
 Can't detect error (Even Parity Check)
Can't detect error (Even Parity Check)In the above example, the the data bits has been changed but as we can see the total count of 1's remain to be even, the error can't be detected even though the message's meaning has been changed. You can visualize the same for odd parity check the number of 1's will remain odd, even if the data bits have been changed and the odd parity check won't be able to detect error.
Explore
Number Systems
Boolean Algebra and Logic Gates
Minimization Techniques
Combinational Circuits
Sequential Circuits
Conversion of Flip-Flop
Register, Counter, and Memory Unit
LMNs and GATE PYQs
My Profile