Depth First Search or DFS for a Graph

In Depth First Search (or DFS) for a graph, we traverse all adjacent vertices one by one. When we traverse an adjacent vertex, we completely finish the traversal of all vertices reachable through that adjacent vertex. This is similar to a tree, where we first completely traverse the left subtree and then move to the right subtree. The key difference is that, unlike trees, graphs may contain cycles (a node may be visited more than once). To avoid processing a node multiple times, we use a boolean visited array.

Example:

Note : There can be multiple DFS traversals of a graph according to the order in which we pick adjacent vertices. Here we pick vertices as per the insertion order.

Input: adj = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]

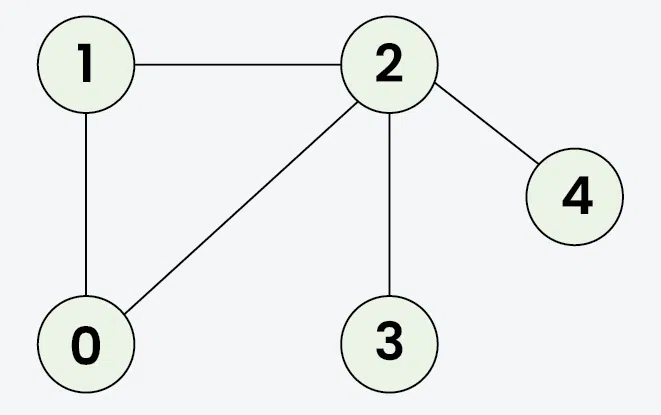
Output: [0 1 2 3 4]
Explanation: The source vertex s is 0. We visit it first, then we visit an adjacent.
Start at 0: Mark as visited. Output: 0
Move to 1: Mark as visited. Output: 1
Move to 2: Mark as visited. Output: 2
Move to 3: Mark as visited. Output: 3 (backtrack to 2)
Move to 4: Mark as visited. Output: 4 (backtrack to 2, then backtrack to 1, then to 0)

Not that there can be more than one DFS Traversals of a Graph. For example, after 1, we may pick adjacent 2 instead of 0 and get a different DFS. Here we pick in the insertion order.

Input: [[2,3,1], [0], [0,4], [0], [2]]

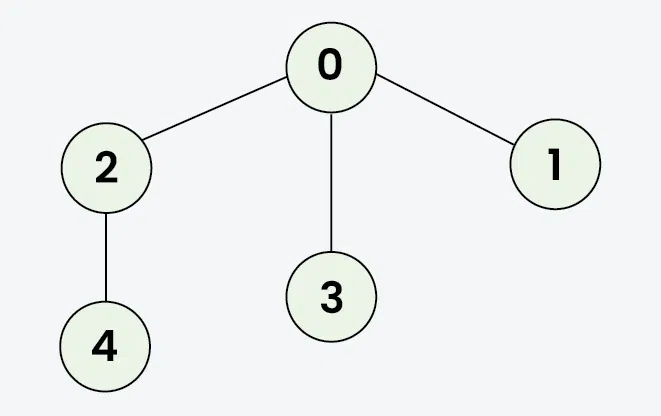
Output: [0 2 4 3 1]
Explanation: DFS Steps:

Start at 0: Mark as visited. Output: 0
Move to 2: Mark as visited. Output: 2
Move to 4: Mark as visited. Output: 4 (backtrack to 2, then backtrack to 0)
Move to 3: Mark as visited. Output: 3 (backtrack to 0)
Move to 1: Mark as visited. Output: 1 (backtrack to 0)

DFS from a Given Source of Undirected Graph:

The algorithm starts from a given source and explores all reachable vertices from the given source. It is similar to Preorder Tree Traversal where we visit the root, then recur for its children. In a graph, there might be loops. So we use an extra visited array to make sure that we do not process a vertex again.

Let us understand the working of Depth First Search with the help of the following Illustration: for the source as 0.

#include <bits/stdc++.h> using namespace std; // Recursive function for DFS traversal void dfsRec(vector<vector<int>> &adj, vector<bool> &visited, int s, vector<int> &res) {  visited[s] = true;  res.push_back(s);  // Recursively visit all adjacent vertices  // that are not visited yet  for (int i : adj[s])  if (visited[i] == false)  dfsRec(adj, visited, i, res); } // Main DFS function that initializes the visited array // and call DFSRec vector<int> DFS(vector<vector<int>> &adj) {  vector<bool> visited(adj.size(), false);  vector<int> res;  dfsRec(adj, visited, 0, res);  return res; } // To add an edge in an undirected graph void addEdge(vector<vector<int>> &adj, int s, int t) {  adj[s].push_back(t);  adj[t].push_back(s); } int main() {  int V = 5;  vector<vector<int>> adj(V);  // Add edges  vector<vector<int>> edges = {{1, 2}, {1, 0}, {2, 0}, {2, 3}, {2, 4}};  for (auto &e : edges)  addEdge(adj, e[0], e[1]);  // Starting vertex for DFS  vector<int> res = DFS(adj); // Perform DFS starting from the source verte 0;  for (int i = 0; i < V; i++)  cout << res[i] << " "; } 

import java.util.*; public class DFSGraph {  // Recursive function for DFS traversal  private static void  dfsRec(ArrayList<ArrayList<Integer> > adj,  boolean[] visited, int s, ArrayList<Integer> res)  {  visited[s] = true;  res.add(s);  // Recursively visit all adjacent vertices that are  // not visited yet  for (int i : adj.get(s)) {  if (!visited[i]) {  dfsRec(adj, visited, i, res);  }  }  }  // Main DFS function that initializes the visited array  // and calls dfsRec  public static ArrayList<Integer>  DFS(ArrayList<ArrayList<Integer> > adj)  {  boolean[] visited = new boolean[adj.size()];  ArrayList<Integer> res = new ArrayList<>();  dfsRec(adj, visited, 0, res);  return res;  }  // To add an edge in an undirected graph  public static void  addEdge(ArrayList<ArrayList<Integer> > adj, int s,  int t)  {  adj.get(s).add(t);  adj.get(t).add(s);  }  public static void main(String[] args)  {  int V = 5;  ArrayList<ArrayList<Integer> > adj  = new ArrayList<>();  // Initialize adjacency list  for (int i = 0; i < V; i++) {  adj.add(new ArrayList<>());  }  // Add edges  int[][] edges= { { 1, 2 },{ 1, 0 },{ 2, 0 },{ 2, 3 },{ 2, 4 } };   for (int[] e : edges)  {  addEdge(adj, e[0], e[1]);  }  // Perform DFS starting from vertex 0  ArrayList<Integer> res = DFS(adj);  for (int i = 0; i < res.size(); i++) {  System.out.print(res.get(i) + " ");  }  } } 

def dfsRec(adj, visited, s, res): visited[s] = True res.append(s) # Recursively visit all adjacent vertices that are not visited yet for i in range(len(adj)): if adj[s][i] == 1 and not visited[i]: dfsRec(adj, visited, i, res) def DFS(adj): visited = [False] * len(adj) res = [] dfsRec(adj, visited, 0, res) # Start DFS from vertex 0 return res def add_edge(adj, s, t): adj[s][t] = 1 adj[t][s] = 1 # Since it's an undirected graph # Driver code V = 5 adj = [[0] * V for _ in range(V)] # Adjacency matrix # Define the edges of the graph edges = [(1, 2), (1, 0), (2, 0), (2, 3), (2, 4)] # Populate the adjacency matrix with edges for s, t in edges: add_edge(adj, s, t) res = DFS(adj) # Perform DFS print(" ".join(map(str, res))) 

using System; using System.Collections.Generic; class DFSGraph {  // Recursive function for DFS traversal  static void DfsRec(List<int>[] adj, bool[] visited,  int s, List<int> res)  {  visited[s] = true;  res.Add(s);  // Recursively visit all adjacent vertices that are  // not visited yet  foreach(int i in adj[s])  {  if (!visited[i]) {  DfsRec(adj, visited, i, res);  }  }  }  // Main DFS function that initializes the visited array  // and calls DfsRec  static List<int> DFS(List<int>[] adj)  {  bool[] visited = new bool[adj.Length];  List<int> res = new List<int>();  DfsRec(adj, visited, 0, res);  return res;  }  // To add an edge in an undirected graph  static void AddEdge(List<int>[] adj, int s, int t)  {  adj[s].Add(t);  adj[t].Add(s);  }  static void Main()  {  int V = 5;  List<int>[] adj = new List<int>[ V ];  // Initialize adjacency list  for (int i = 0; i < V; i++) {  adj[i] = new List<int>();  }  // Add edges  int[, ] edges = {  { 1, 2 }, { 1, 0 }, { 2, 0 }, { 2, 3 }, { 2, 4 }  };  for (int i = 0; i < edges.GetLength(0); i++) {  AddEdge(adj, edges[i, 0], edges[i, 1]);  }  // Perform DFS starting from vertex 0  List<int> res = DFS(adj);  foreach(int i in res) { Console.Write(i + " "); }  } } 

function dfsRec(adj, visited, s, res) {  visited[s] = true;  res.push(s);  // Recursively visit all adjacent vertices that are not  // visited yet  for (let i = 0; i < adj.length; i++) {  if (adj[s][i] === 1 && !visited[i]) {  dfsRec(adj, visited, i, res);  }  } } function DFS(adj) {  let visited = new Array(adj.length).fill(false);  let res = [];  dfsRec(adj, visited, 0, res); // Start DFS from vertex 0  return res; } function addEdge(adj, s, t) {  adj[s][t] = 1;  adj[t][s] = 1; // Since it's an undirected graph } // Driver code let V = 5; let adj = Array.from(  {length : V},  () => new Array(V).fill(0)); // Adjacency matrix // Define the edges of the graph let edges =  [ [ 1, 2 ], [ 1, 0 ], [ 2, 0 ], [ 2, 3 ], [ 2, 4 ] ]; // Populate the adjacency matrix with edges edges.forEach(([ s, t ]) => addEdge(adj, s, t)); let res = DFS(adj); // Perform DFS console.log(res.join(" ")); 

0 1 2 3 4 

Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Auxiliary Space: O(V + E), since an extra visited array of size V is required, And stack size for recursive calls to dfsRec function.

Please refer Complexity Analysis of Depth First Search for details.

DFS for Complete Traversal of Disconnected Undirected Graph

The above implementation takes a source as an input and prints only those vertices that are reachable from the source and would not print all vertices in case of disconnected graph. Let us now talk about the algorithm that prints all vertices without any source and the graph maybe disconnected.

The idea is simple, instead of calling DFS for a single vertex, we call the above implemented DFS for all all non-visited vertices one by one.

#include <bits/stdc++.h> using namespace std; void addEdge(vector<vector<int>> &adj, int s, int t) {  adj[s].push_back(t);  adj[t].push_back(s); } // Recursive function for DFS traversal void dfsRec(vector<vector<int>> &adj, vector<bool> &visited, int s, vector<int> &res) {  // Mark the current vertex as visited  visited[s] = true;  res.push_back(s);  // Recursively visit all adjacent vertices that are not visited yet  for (int i : adj[s])  if (visited[i] == false)  dfsRec(adj, visited, i, res); } // Main DFS function to perform DFS for the entire graph vector<int> DFS(vector<vector<int>> &adj) {  vector<bool> visited(adj.size(), false);  vector<int> res;  // Loop through all vertices to handle disconnected graph  for (int i = 0; i < adj.size(); i++)  {  if (visited[i] == false)  {  // If vertex i has not been visited,  // perform DFS from it  dfsRec(adj, visited, i, res);  }  }  return res; } int main() {  int V = 6;  // Create an adjacency list for the graph  vector<vector<int>> adj(V);  // Define the edges of the graph  vector<vector<int>> edges = {{1, 2}, {2, 0}, {0, 3}, {4, 5}};  // Populate the adjacency list with edges  for (auto &e : edges)  addEdge(adj, e[0], e[1]);  vector<int> res = DFS(adj);  for (auto it : res)  cout << it << " ";  return 0; } 

import java.util.*; public class GfG {  // Function to add an edge to the adjacency list  public static void  addEdge(ArrayList<ArrayList<Integer> > adj, int s,  int t)  {  adj.get(s).add(t);  adj.get(t).add(s);  }  // Recursive function for DFS traversal  private static void  dfsRec(ArrayList<ArrayList<Integer> > adj,  boolean[] visited, int s, ArrayList<Integer> res)  {  visited[s] = true;  res.add(s);  // Recursively visit all adjacent vertices that are  // not visited yet  for (int i : adj.get(s)) {  if (!visited[i]) {  dfsRec(adj, visited, i, res);  }  }  }  // Main DFS function to perform DFS for the entire graph  public static ArrayList<Integer>  DFS(ArrayList<ArrayList<Integer> > adj)  {  boolean[] visited = new boolean[adj.size()];  ArrayList<Integer> res = new ArrayList<>();  // Loop through all vertices to handle disconnected  // graphs  for (int i = 0; i < adj.size(); i++) {  if (!visited[i]) {  dfsRec(adj, visited, i, res);  }  }  return res;  }  public static void main(String[] args)  {  int V = 6;  // Create an adjacency list for the graph  ArrayList<ArrayList<Integer> > adj  = new ArrayList<>();  // Initialize adjacency list  for (int i = 0; i < V; i++) {  adj.add(new ArrayList<>());  }  // Define the edges of the graph  int[][] edges  = { { 1, 2 }, { 2, 0 }, { 0, 3 }, { 4, 5 } };  // Populate the adjacency list with edges  for (int[] e : edges) {  addEdge(adj, e[0], e[1]);  }  // Perform DFS  ArrayList<Integer> res = DFS(adj);  // Print the DFS traversal result  for (int num : res) {  System.out.print(num + " ");  }  } } 

# Create an adjacency list for the graph from collections import defaultdict def add_edge(adj, s, t): adj[s].append(t) adj[t].append(s) # Recursive function for DFS traversal def dfs_rec(adj, visited, s, res): # Mark the current vertex as visited visited[s] = True res.append(s) # Recursively visit all adjacent vertices that are not visited yet for i in adj[s]: if not visited[i]: dfs_rec(adj, visited, i, res) # Main DFS function to perform DFS for the entire graph def dfs(adj): visited = [False] * len(adj) res = [] # Loop through all vertices to handle disconnected graph for i in range(len(adj)): if not visited[i]: # If vertex i has not been visited, # perform DFS from it dfs_rec(adj, visited, i, res) return res V = 6 # Create an adjacency list for the graph adj = defaultdict(list) # Define the edges of the graph edges = [[1, 2], [2, 0], [0, 3], [4, 5]] # Populate the adjacency list with edges for e in edges: add_edge(adj, e[0], e[1]) res = dfs(adj) print(' '.join(map(str, res))) 

using System; using System.Collections.Generic; class GfG {  // Function to add an edge to the adjacency list  static void AddEdge(List<int>[] adj, int s, int t)  {  adj[s].Add(t);  adj[t].Add(s);  }  // Recursive function for DFS traversal  static void DfsRec(List<int>[] adj, bool[] visited,  int s, List<int> res)  {  visited[s] = true;  res.Add(s);  // Recursively visit all adjacent vertices that are  // not visited yet  foreach(int i in adj[s])  {  if (!visited[i]) {  DfsRec(adj, visited, i, res);  }  }  }  // Main DFS function to perform DFS for the entire graph  static List<int> DFS(List<int>[] adj)  {  bool[] visited = new bool[adj.Length];  List<int> res = new List<int>();  // Loop through all vertices to handle disconnected  // graphs  for (int i = 0; i < adj.Length; i++) {  if (!visited[i]) {  DfsRec(adj, visited, i, res);  }  }  return res;  }  static void Main()  {  int V = 6;  // Create an adjacency list for the graph  List<int>[] adj = new List<int>[ V ];  // Initialize adjacency list  for (int i = 0; i < V; i++) {  adj[i] = new List<int>();  }  // Define the edges of the graph  int[, ] edges  = { { 1, 2 }, { 2, 0 }, { 0, 3 }, { 4, 5 } };  // Populate the adjacency list with edges  for (int i = 0; i < edges.GetLength(0); i++) {  AddEdge(adj, edges[i, 0], edges[i, 1]);  }  // Perform DFS  List<int> res = DFS(adj);  // Print the DFS traversal result  foreach(int num in res)  {  Console.Write(num + " ");  }  } } 

function addEdge(adj, s, t) {  adj[s].push(t);  adj[t].push(s); } // Recursive function for DFS traversal function dfsRec(adj, visited, s, res) {  visited[s] = true;  res.push(s);  // Recursively visit all adjacent vertices that are not visited yet  for (let i of adj[s]) {  if (!visited[i]) {  dfsRec(adj, visited, i, res);  }  } } // Main DFS function to perform DFS for the entire graph function DFS(adj) {  let visited = new Array(adj.length).fill(false);  let res = [];  // Loop through all vertices to handle disconnected graphs  for (let i = 0; i < adj.length; i++) {  if (!visited[i]) {  dfsRec(adj, visited, i, res);  }  }  return res; } // Main Execution let V = 6; // Create an adjacency list for the graph let adj = Array.from({ length: V }, () => []); let edges = [[1, 2], [2, 0], [0, 3], [4, 5]]; // Populate the adjacency list with edges for (let e of edges) {  addEdge(adj, e[0], e[1]); } // Perform DFS let res = DFS(adj); // Print the DFS traversal result console.log(res.join(" ")); 

0 2 1 3 4 5 

Time complexity: O(V + E). Note that the time complexity is same here because we visit every vertex at most once and every edge is traversed at most once (in directed) and twice in undirected.
Auxiliary Space: O(V + E), since an extra visited array of size V is required, And stack size for recursive calls to dfsRec function.

Related Articles:

• Depth First Search or DFS on Directed Graph
• Breadth First Search or BFS for a Graph