C++ Program To Find Transpose of a Matrix

Last Updated : 23 Jul, 2025

Transpose of a matrix is obtained by changing rows to columns and columns to rows. In other words, the transpose of A[][] is obtained by changing A[i][j] to A[j][i].

Example:

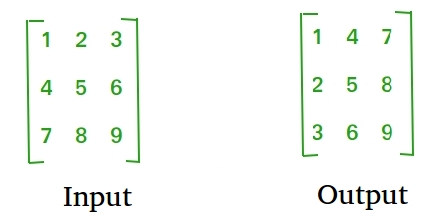
matrix-transpose

1. For Square Matrix

The below program finds the transpose of A[][] and stores the result in B[][], we can change N for a different dimension.

C++

// C++ Program to find the transpose  // of a matrix #include <bits/stdc++.h>  using namespace std;  #define N 4 // This function stores transpose  // of A[][] in B[][] void transpose(int A[][N],   int B[][N]) {  int i, j;  for (i = 0; i < N; i++)  for (j = 0; j < N; j++)  B[i][j] = A[j][i]; } // Driver code int main() {  int A[N][N] = {{1, 1, 1, 1},  {2, 2, 2, 2},  {3, 3, 3, 3},  {4, 4, 4, 4}};  int B[N][N], i, j;  transpose(A, B);  cout << "Result matrix is \n";  for (i = 0; i < N; i++)  {  for (j = 0; j < N; j++)  cout << " " << B[i][j];  cout <<"\n";  }  return 0; }

Output

Result matrix is 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4

The complexity of the above method

Time Complexity: O(N*N) as two nested loops are running.

Space Complexity: O(N*N) as 2d array is created to store transpose.

2. For Rectangular Matrix

The below program finds the transpose of A[][] and stores the result in B[][].

C++

// C++ program to find transpose  // of a matrix #include <bits/stdc++.h> using namespace std; #define M 3 #define N 4 // This function stores transpose  // of A[][] in B[][] void transpose(int A[][N], int B[][M]) {  int i, j;  for(i = 0; i < N; i++)  for(j = 0; j < M; j++)  B[i][j] = A[j][i]; } // Driver code int main() {  int A[M][N] = {{1, 1, 1, 1},  {2, 2, 2, 2},  {3, 3, 3, 3}};  // Note dimensions of B[][]  int B[N][M], i, j;  transpose(A, B);  cout << "Result matrix is \n";  for(i = 0; i < N; i++)  {  for(j = 0; j < M; j++)  cout << " " << B[i][j];    cout << "\n";  }  return 0; }

Output

Result matrix is 1 2 3 1 2 3 1 2 3 1 2 3

The complexity of the above method

Time Complexity: O(N*M) as two nested loops are running.

Space Complexity: O(N*M) as 2d array is created to store transpose.

3. In-Place for Square Matrix

Below is the implementation of the method:

C++

// C++ program to implement // the above approach #include <bits/stdc++.h> using namespace std; #define N 4 // Converts A[][] to its transpose void transpose(int A[][N]) {  for (int i = 0; i < N; i++)  for (int j = i+1; j < N; j++)  swap(A[i][j], A[j][i]); } // Driver code int main() {  int A[N][N] = {{1, 1, 1, 1},  {2, 2, 2, 2},  {3, 3, 3, 3},  {4, 4, 4, 4}};  transpose(A);  printf("Modified matrix is \n");  for (int i = 0; i < N; i++)  {  for (int j = 0; j < N; j++)  printf("%d ", A[i][j]);  printf("\n");  }  return 0; }

Output

Modified matrix is 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4

The complexity of the above method

Time complexity: O(n)

Transpose has a time complexity of O(n + m), where n is the number of columns and m is the number of non-zero elements in the matrix.
The computational time for transposing of a matrix using an identity matrix as a reference matrix is O(m*n).
Suppose, if the given matrix is a square matrix, the running time will be O(n²).

Auxiliary space: O(1).