C++ Program for Topological Sorting

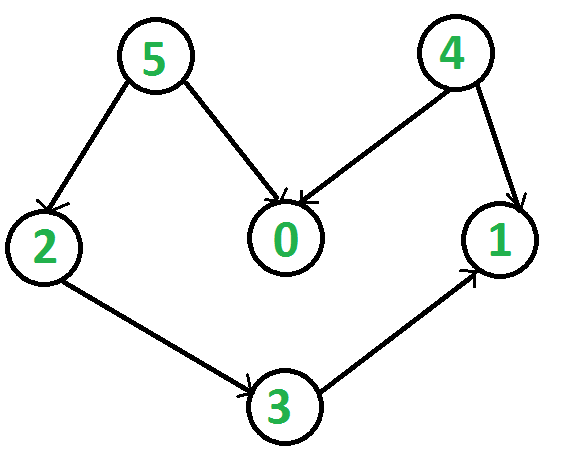
// A C++ program to print topological sorting of a DAG #include <iostream> #include <list> #include <stack> using namespace std; // Class to represent a graph class Graph {  int V; // No. of vertices'  // Pointer to an array containing adjacency listsList  list<int>* adj;  // A function used by topologicalSort  void topologicalSortUtil(int v, bool visited[], stack<int>& Stack); public:  Graph(int V); // Constructor  // function to add an edge to graph  void addEdge(int v, int w);  // prints a Topological Sort of the complete graph  void topologicalSort(); }; Graph::Graph(int V) {  this->V = V;  adj = new list<int>[V]; } void Graph::addEdge(int v, int w) {  adj[v].push_back(w); // Add w to v’s list. } // A recursive function used by topologicalSort void Graph::topologicalSortUtil(int v, bool visited[],  stack<int>& Stack) {  // Mark the current node as visited.  visited[v] = true;  // Recur for all the vertices adjacent to this vertex  list<int>::iterator i;  for (i = adj[v].begin(); i != adj[v].end(); ++i)  if (!visited[*i])  topologicalSortUtil(*i, visited, Stack);  // Push current vertex to stack which stores result  Stack.push(v); } // The function to do Topological Sort. It uses recursive // topologicalSortUtil() void Graph::topologicalSort() {  stack<int> Stack;  // Mark all the vertices as not visited  bool* visited = new bool[V];  for (int i = 0; i < V; i++)  visited[i] = false;  // Call the recursive helper function to store Topological  // Sort starting from all vertices one by one  for (int i = 0; i < V; i++)  if (visited[i] == false)  topologicalSortUtil(i, visited, Stack);  // Print contents of stack  while (Stack.empty() == false) {  cout << Stack.top() << " ";  Stack.pop();  } } // Driver program to test above functions int main() {  // Create a graph given in the above diagram  Graph g(6);  g.addEdge(5, 2);  g.addEdge(5, 0);  g.addEdge(4, 0);  g.addEdge(4, 1);  g.addEdge(2, 3);  g.addEdge(3, 1);  cout << "Following is a Topological Sort of the given graph: ";  g.topologicalSort();  return 0; }