C Program to Implement AVL Tree
Last Updated : 23 Jul, 2025
In C, AVL trees are self-balancing binary search trees. They maintain a balance by ensuring that the difference between the heights of their left subtrees and the right subtrees can be either 0, 1 or -1 and whenever this height property is violated, the tree balances itself using the different rotations. This balancing allows for efficient search, insertion, and deletion operations with a time complexity of O(log n) for every case. In this article, we will learn how to implement AVL tree in C programming language
AVL Tree in C
An AVL tree is a self-balancing binary search tree that was created by Adelson-Velsky and Landis, hence the name AVL. It is a height balanced tree that keeps the difference between the height of the left and right subtrees in the range [-1, 0, 1]. This difference is called balanced factor and tree is said to be unbalanced when this balance factor is outside the specified range. Unbalanced tree is balanced through specific rotation operations during insertions and deletions.
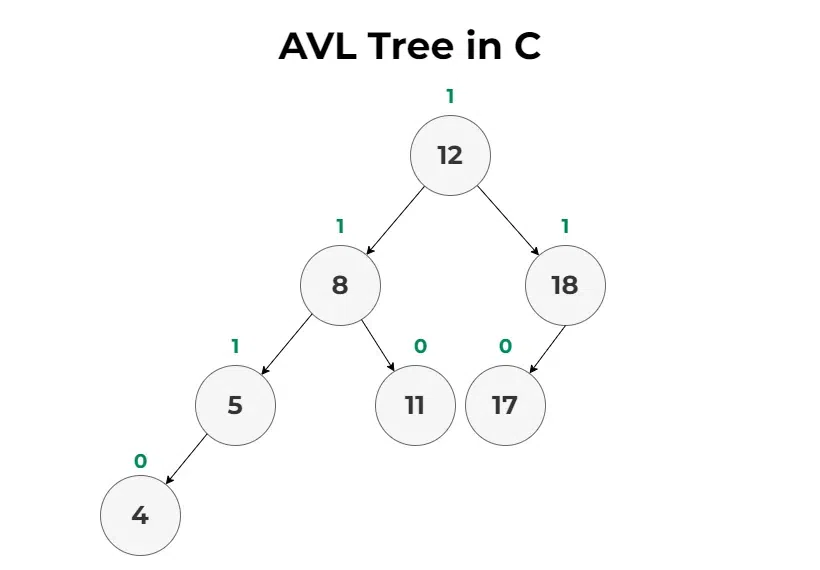
Representation of AVL Tree in C
In C, an AVL tree node is typically defined using a struct. Each node contains the data, pointers to its left and right children, and an integer to store its height.
struct AVLNode {
int key;
struct AVLNode* left;
struct AVLNode* right;
int height;
};AVL Tree Rotations in C
Rotations are the most important part of the working of the AVL tree. They are responsible for maintaining the balance in the AVL tree. There are 4 types of rotations based on the 4 possible cases:
- Right Rotation (RR)
- Left Rotation (LL)
- Left-Right Rotation (LR)
- Right-Left Rotation (RL)
Right Rotation (RR)
The RR rotation is applied when a node becomes unbalanced due to an insertion into the right subtree of its right child. This type of imbalance is called Left Imbalance. The solution to it is to take the unbalanced node, and rotate the top edge (that is connected with parent) 90° to the right (clockwise).
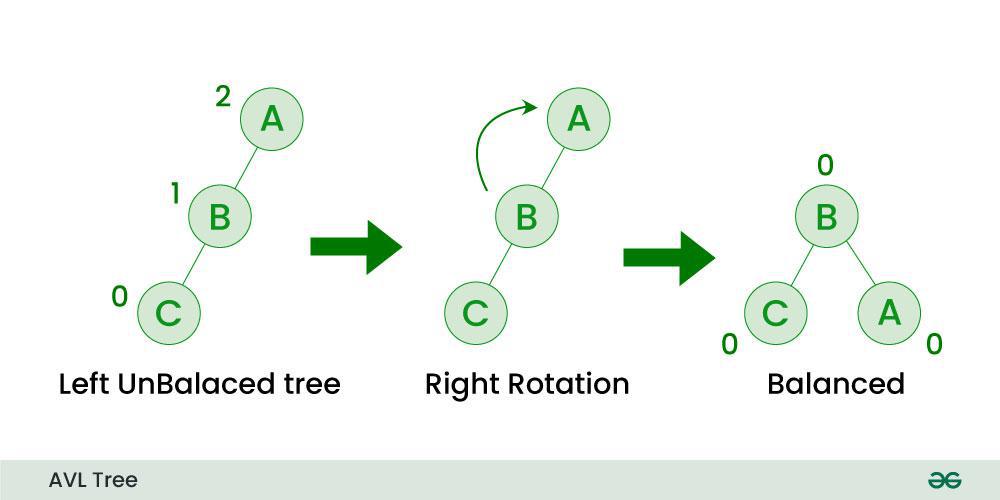 Right Rotation - RR in AVL Tree
Right Rotation - RR in AVL TreeLeft Rotation (LL)
The LL rotation is used in an AVL tree to balance a node that becomes unbalanced due to an insertion into the left subtree of its left child. It is called Left Imbalance. The solution to it is to take the unbalanced node, and rotate the top edge (that is connected with parent) 90° to the left(anti-clockwise).
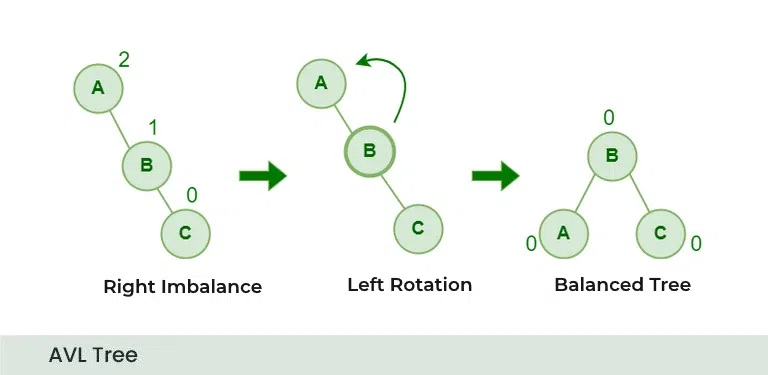 Left Rotation - RR in AVL Tree
Left Rotation - RR in AVL TreeLeft-Right Rotation (LR)
A right-left rotation is used when a left child of a node is right-heavy. It helps in balancing the tree after a double imbalance, which is another specific insertion case. We first perform a left rotation on the left child and follow it up with a right rotation on the original node.
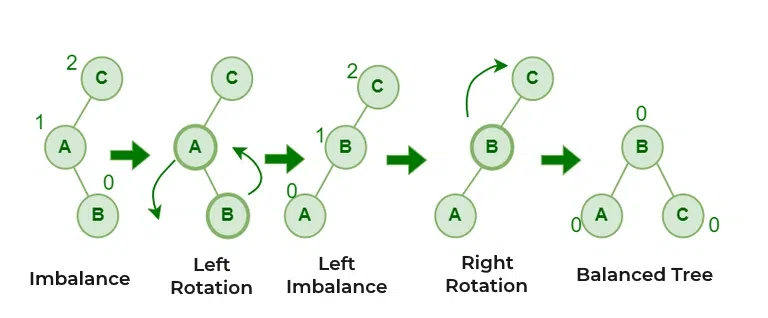 Left Right Rotation - LR in AVL Tree
Left Right Rotation - LR in AVL TreeRight-Left Rotation (RL)
The right left rotation is performed when a right child of a node is left-heavy. We perform a right rotation on the right child and follow it up with a left rotation on the original node.
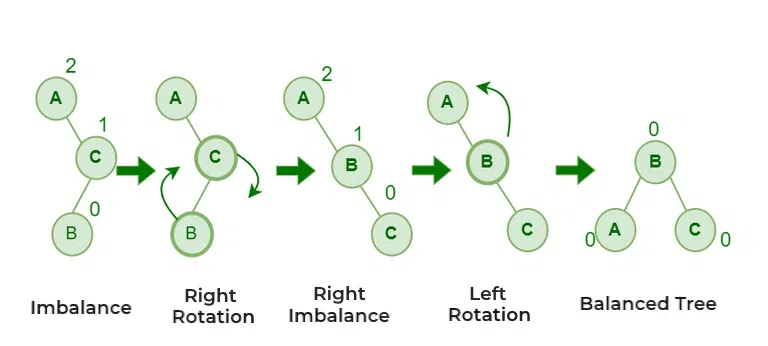 Right Left Rotation - RL in AVL Tree
Right Left Rotation - RL in AVL TreeImplementation of AVL Tree in C
We will implement the AVL tree along with its basic operations. Following are the basic operations of AVL tree:
| Operation | Description | Time Complexity | Space Complexity |
|---|
| Search | Finds a specific value in the tree. | O(log n) | O(log n) |
|---|
| Insert | Adds a new value to the tree while maintaining balance. | O(log n) | O(1) |
|---|
| Delete | Removes a specific value from the tree and maintains balance. | O(log n) | O(1) |
|---|
Search Operation Implementation
We implement the search operation on AVL tree using the following algorithm:
- If root is null or key is present at root, return root.
- If key is smaller than root’s key, search in left subtree.
- If key is larger than root’s key, search in right subtree.
Insert Operation Implementation
Insert operation may create an imbalance in the tree which should be handled by the program according to the case.
- If the current node is
NULL, create a new node with the given key. - If the key is less than the current node’s key, recursively insert the key in the left subtree.
- If the key is greater than the current node’s key, recursively insert the key in the right subtree.
- After insertion, update the height of the current node.
- Calculate the balance factor of the current node.
- If the balance factor is greater than 1 (left-heavy), check for Left-Left (LL) or Left-Right (LR) case:
- LL Case: If the left child’s key is greater than the inserted key, perform a right rotation.
- LR Case: If the left child’s key is less than the inserted key, perform a left rotation on the left child, then a right rotation on the current node.
- If the balance factor is less than -1 (right-heavy), check for Right-Right (RR) or Right-Left (RL) case:
- RR Case: If the right child’s key is less than the inserted key, perform a left rotation.
- RL Case: If the right child’s key is greater than the inserted key, perform a right rotation on the right child, then a left rotation on the current node.
Delete Operation Implementation
- If the node to be deleted is not found, return
NULL. - If the key to be deleted is less than the current node’s key, recursively delete the key in the left subtree.
- If the key to be deleted is greater than the current node’s key, recursively delete the key in the right subtree.
- If the key to be deleted is equal to the current node’s key:
- If the node has only one child or no child, replace the node with its child.
- If the node has two children, find the in order successor (smallest in the right subtree), copy its key to the node, and delete the inorder successor.
- After deletion, update the height of the current node.
- Calculate the balance factor of the current node.
- Check and fix imbalance just like in insertion.
- Return the node after performing necessary rotations to balance the tree.
C Program to Implement AVL Tree
C // C program to implement the avl tree #include <stdio.h> #include <stdlib.h> // AVL Tree node struct Node { int key; struct Node* left; struct Node* right; int height; }; // Function to get height of the node int getHeight(struct Node* n) { if (n == NULL) return 0; return n->height; } // Function to create a new node struct Node* createNode(int key) { struct Node* node = (struct Node*)malloc(sizeof(struct Node)); node->key = key; node->left = NULL; node->right = NULL; node->height = 1; // New node is initially added at leaf return node; } // Utility function to get the maximum of two integers int max(int a, int b) { return (a > b) ? a : b; } // Function to get balance factor of a node int getBalanceFactor(struct Node* n) { if (n == NULL) return 0; return getHeight(n->left) - getHeight(n->right); } // Right rotation function struct Node* rightRotate(struct Node* y) { struct Node* x = y->left; struct Node* T2 = x->right; // Perform rotation x->right = y; y->left = T2; // Update heights y->height = max(getHeight(y->left), getHeight(y->right)) + 1; x->height = max(getHeight(x->left), getHeight(x->right)) + 1; return x; } // Left rotation function struct Node* leftRotate(struct Node* x) { struct Node* y = x->right; struct Node* T2 = y->left; // Perform rotation y->left = x; x->right = T2; // Update heights x->height = max(getHeight(x->left), getHeight(x->right)) + 1; y->height = max(getHeight(y->left), getHeight(y->right)) + 1; return y; } // Function to insert a key into AVL tree struct Node* insert(struct Node* node, int key) { // 1. Perform standard BST insertion if (node == NULL) return createNode(key); if (key < node->key) node->left = insert(node->left, key); else if (key > node->key) node->right = insert(node->right, key); else // Equal keys are not allowed in BST return node; // 2. Update height of this ancestor node node->height = 1 + max(getHeight(node->left), getHeight(node->right)); // 3. Get the balance factor of this ancestor node to // check whether this node became unbalanced int balance = getBalanceFactor(node); // 4. If the node becomes unbalanced, then there are 4 // cases // Left Left Case if (balance > 1 && key < node->left->key) return rightRotate(node); // Right Right Case if (balance < -1 && key > node->right->key) return leftRotate(node); // Left Right Case if (balance > 1 && key > node->left->key) { node->left = leftRotate(node->left); return rightRotate(node); } // Right Left Case if (balance < -1 && key < node->right->key) { node->right = rightRotate(node->right); return leftRotate(node); } // Return the (unchanged) node pointer return node; } // Function to perform preorder traversal of AVL tree void inOrder(struct Node* root) { if (root != NULL) { inOrder(root->left); printf("%d ", root->key); inOrder(root->right); } } // Main function int main() { struct Node* root = NULL; // Inserting nodes root = insert(root, 1); root = insert(root, 2); root = insert(root, 4); root = insert(root, 5); root = insert(root, 6); root = insert(root, 3); // Print preorder traversal of the AVL tree printf("Inorder traversal of AVL tree: "); inOrder(root); return 0; }
Output
Inorder traversal of AVL tree: 1 2 3 4 5 6
Related Articles:
Explore
C Basics
Arrays & Strings
Pointers and Structures
Memory Management
File & Error Handling
Advanced Concepts
My Profile