Add and Remove vertex in Adjacency List representation of Graph
Last Updated : 29 Jan, 2025
Prerequisites: Linked List, Graph Data Structure
In this article, adding and removing a vertex is discussed in a given adjacency list representation. Let the Directed Graph be: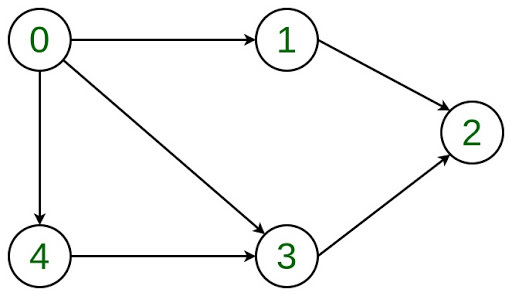 
The graph can be represented in the Adjacency List representation as: 
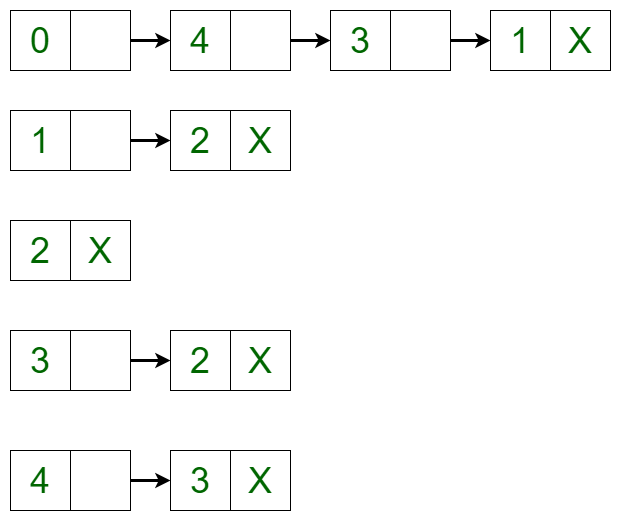It is a Linked List representation where the head of the linked list is a vertex in the graph and all the connected nodes are the vertices to which the first vertex is connected. For example, from the graph, it is clear that vertex 0 is connected to vertex 4, 3 and 1. The same is represented in the adjacency list(or Linked List) representation.
Adding a Vertex in the Adjacency List:
To add a vertex in the graph, the adjacency list can be iterated to the place where the insertion is required and the new node can be created using linked list implementation. For example, if 5 needs to be added between vertex 2 and vertex 3 such that vertex 3 points to vertex 5 and vertex 5 points to vertex 2, then a new edge is created between vertex 5 and vertex 3 and a new edge is created from vertex 5 and vertex 2. After adding the vertex, the adjacency list changes to:
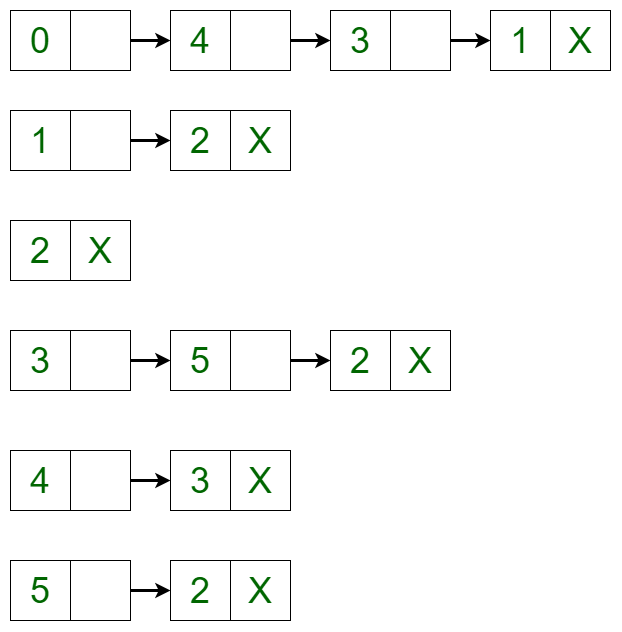
Removing a Vertex in Adjacency List:
To delete a vertex in the graph, iterate through the list of each vertex if an edge is present or not. If the edge is present, then delete the vertex in the same way as delete is performed in a linked list. For example, the adjacency list translates to the below list if vertex 4 is deleted from the list:
Below is the implementation of the above approach:
C++ #include <iostream> using namespace std; // Node to store adjacency list class AdjNode { public: int vertex; AdjNode* next; AdjNode(int data) { vertex = data; next = NULL; } }; // Adjacency List representation class AdjList { private: int v; AdjNode** graph; public: AdjList(int vertices) { v = vertices; graph = new AdjNode*[v]; for (int i = 0; i < v; ++i) graph[i] = NULL; } // Function to add an edge from a source vertex // to a destination vertex void addEdge(int source, int destination) { AdjNode* node = new AdjNode(destination); node->next = graph[source]; graph[source] = node; } // Function to add a vertex between two vertices void addVertex(int vk, int source, int destination) { addEdge(source, vk); addEdge(vk, destination); } // Function to print the graph void printGraph() { for (int i = 0; i < v; ++i) { if (graph[i] == NULL) continue; cout << i << " "; AdjNode* temp = graph[i]; while (temp != NULL) { cout << "-> " << temp->vertex << " "; temp = temp->next; } cout << endl; } } // Function to delete a vertex void delVertex(int k) { // Iterate through all the vertices of the graph for (int i = 0; i < v; ++i) { AdjNode *curr = graph[i], *prev = nullptr; if (i == k) { graph[i] = nullptr; while (curr != nullptr) { AdjNode* next = curr->next; delete (curr); curr = next; } } else { while (curr != nullptr) { if (curr->vertex == k) { if (prev == nullptr) { // If k is at the start of the list, remove it graph[i] = curr->next; } else { // If k is in the middle or end, remove it prev->next = curr->next; } delete curr; break; } prev = curr; curr = curr->next; } } } } }; int main() { int V = 6; AdjList graph(V); graph.addEdge(0, 1); graph.addEdge(0, 3); graph.addEdge(0, 4); graph.addEdge(1, 2); graph.addEdge(3, 2); graph.addEdge(4, 3); cout << "Initial adjacency list" << endl; graph.printGraph(); // Add vertex graph.addVertex(5, 3, 2); cout << "Adjacency list after adding vertex" << endl; graph.printGraph(); // Delete vertex graph.delVertex(4); cout << "Adjacency list after deleting vertex" << endl; graph.printGraph(); return 0; } // GFG // JAVA implementation of the above approach // Implementing Linked List representation import java.util.*; // Node to store adjacency list class AdjNode { int vertex; AdjNode next; public AdjNode(int data) { vertex = data; next = null; } } // Adjacency List representation class AdjList { private int v; private AdjNode[] graph; public AdjList(int vertices) { v = vertices; graph = new AdjNode[v]; for (int i = 0; i < v; ++i) { graph[i] = null; } } // Function to add an edge from a source vertex // to a destination vertex public void addEdge(int source, int destination) { AdjNode node = new AdjNode(destination); node.next = graph[source]; graph[source] = node; } // Function to add a vertex between two vertices public void addVertex(int vk, int source, int destination) { addEdge(source, vk); addEdge(vk, destination); } // Function to print the graph public void printGraph() { for (int i = 0; i < v; ++i) { System.out.print(i + " "); AdjNode temp = graph[i]; while (temp != null) { System.out.print("-> " + temp.vertex + " "); temp = temp.next; } System.out.println(); } } // Function to delete a vertex public void delVertex(int k) { // Iterate through all the vertices of the graph for (int i = 0; i < v; ++i) { AdjNode curr = graph[i], prev = null; if (i == k) { graph[i] = null; } else { while (curr != null) { if (curr.vertex == k) { if (prev == null) { // If k is at the start of the list, remove it graph[i] = curr.next; } else { // If k is in the middle or end, remove it prev.next = curr.next; } break; } prev = curr; curr = curr.next; } } } } } public class Main { public static void main(String[] args) { int V = 6; AdjList graph = new AdjList(V); graph.addEdge(0, 1); graph.addEdge(0, 3); graph.addEdge(0, 4); graph.addEdge(1, 2); graph.addEdge(3, 2); graph.addEdge(4, 3); System.out.println("Initial adjacency list"); graph.printGraph(); // Add vertex graph.addVertex(5, 3, 2); System.out.println("Adjacency list after adding vertex"); graph.printGraph(); // Delete vertex graph.delVertex(4); System.out.println("Adjacency list after deleting vertex"); graph.printGraph(); } } # Python implementation of the above approach # Implementing Linked List representation class AdjNode(object): def __init__(self, data): self.vertex = data self.next = None # Adjacency List representation class AdjList(object): def __init__(self, vertices): self.v = vertices self.graph = [None] * self.v # Function to add an edge from a source vertex # to a destination vertex def addedge(self, source, destination): node = AdjNode(destination) node.next = self.graph[source] self.graph[source] = node # Function to call the above function. def addvertex(self, vk, source, destination): self.addedge(source, vk) self.addedge(vk, destination) # Function to print the graph def print_graph(self): for i in range(self.v): print(i, end=" ") temp = self.graph[i] while temp: print("->", temp.vertex, end=" ") temp = temp.next print("\n") # Function to delete a vertex def delVertex(self, k): for i in range(self.v): curr = self.graph[i] prev = None if i == k: self.graph[i] = None else: while curr is not None: if curr.vertex == k: if prev is None: # If k is at the start of the list, remove it self.graph[i] = curr.next else: # If k is in the middle or end, remove it prev.next = curr.next break prev = curr curr = curr.next # Driver code if __name__ == "__main__": V = 6 graph = AdjList(V) graph.addedge(0, 1) graph.addedge(0, 3) graph.addedge(0, 4) graph.addedge(1, 2) graph.addedge(3, 2) graph.addedge(4, 3) print("Initial adjacency list") graph.print_graph() # Add vertex graph.addvertex(5, 3, 2) print("Adjacency list after adding vertex") graph.print_graph() # Delete vertex graph.delVertex(4) print("Adjacency list after deleting vertex") graph.print_graph() // C# implementation of the above approach Implementing // Linked List representation using System; // Node to store adjacency list class AdjNode { public int vertex; public AdjNode next; public AdjNode(int data) { vertex = data; next = null; } } // Adjacency List representation class AdjList { private int v; private AdjNode[] graph; public AdjList(int vertices) { v = vertices; graph = new AdjNode[v]; for (int i = 0; i < v; ++i) { graph[i] = null; } } // Function to add an edge from a source vertex // to a destination vertex public void addEdge(int source, int destination) { AdjNode node = new AdjNode(destination); node.next = graph[source]; graph[source] = node; } // Function to add a vertex between two vertices public void addVertex(int vk, int source, int destination) { addEdge(source, vk); addEdge(vk, destination); } // Function to print the graph public void printGraph() { for (int i = 0; i < v; ++i) { Console.Write(i + " "); AdjNode temp = graph[i]; while (temp != null) { Console.Write("-> " + temp.vertex + " "); temp = temp.next; } Console.WriteLine(); } } // Function to delete a vertex public void delVertex(int k) { // Iterate through all the vertices of the graph for (int i = 0; i < v; ++i) { AdjNode curr = graph[i]; AdjNode prev = null; if (i == k) { graph[i] = null; } else { while (curr != null) { if (curr.vertex == k) { if (prev == null) { // If k is at the start of the list, remove it graph[i] = curr.next; } else { // If k is in the middle or end, remove it prev.next = curr.next; } break; } prev = curr; curr = curr.next; } } } } } public class GFG { static public void Main() { // Code int V = 6; AdjList graph = new AdjList(V); graph.addEdge(0, 1); graph.addEdge(0, 3); graph.addEdge(0, 4); graph.addEdge(1, 2); graph.addEdge(3, 2); graph.addEdge(4, 3); Console.WriteLine("Initial adjacency list"); graph.printGraph(); // Add vertex graph.addVertex(5, 3, 2); Console.WriteLine( "Adjacency list after adding vertex"); graph.printGraph(); // Delete vertex graph.delVertex(4); Console.WriteLine("Adjacency list after deleting vertex"); graph.printGraph(); } } // JavaScript code implementation: // Node to store adjacency list class AdjNode { constructor(data) { this.vertex = data; this.next = null; } } // Adjacency List representation class AdjList { constructor(vertices) { this.v = vertices; this.graph = new Array(this.v).fill(null); } // Function to add an edge from a source vertex to a destination vertex addEdge(source, destination) { const node = new AdjNode(destination); node.next = this.graph[source]; this.graph[source] = node; } // Function to add a vertex between two vertices addVertex(vk, source, destination) { this.addEdge(source, vk); this.addEdge(vk, destination); } // Function to print the graph printGraph() { for (let i = 0; i < this.v; ++i) { let str = i + " "; let temp = this.graph[i]; while (temp != null) { str += "-> " + temp.vertex + " "; temp = temp.next; } console.log(str); } } // Function to delete a vertex delVertex(k) { // Iterate through all the vertices of the graph for (let i = 0; i < this.v; ++i) { let curr = this.graph[i]; let prev = null; if (i === k) { this.graph[i] = null; } else { while (curr !== null) { if (curr.vertex === k) { if (prev === null) { // If k is at the start of the list, remove it this.graph[i] = curr.next; } else { // If k is in the middle or end, remove it prev.next = curr.next; } break; } prev = curr; curr = curr.next; } } } } } const V = 6; const graph = new AdjList(V); graph.addEdge(0, 1); graph.addEdge(0, 3); graph.addEdge(0, 4); graph.addEdge(1, 2); graph.addEdge(3, 2); graph.addEdge(4, 3); console.log("Initial adjacency list"); graph.printGraph(); // Add vertex graph.addVertex(5, 3, 2); console.log("Adjacency list after adding vertex"); graph.printGraph(); // Delete vertex graph.delVertex(4); console.log("Adjacency list after deleting vertex"); graph.printGraph(); OutputInitial adjacency list 0 -> 4 -> 3 -> 1 1 -> 2 3 -> 2 4 -> 3 Adjacency list after adding vertex 0 -> 4 -> 3 -> 1 1 -> 2 3 -> 5 -> 2 4 -> 3 5 -> 2 Adjacency list after deleting vertex 0 -> 3 -...
Similar Reads
Add and Remove vertex in Adjacency Matrix representation of Graph A graph is a presentation of a set of entities where some pairs of entities are linked by a connection. Interconnected entities are represented by points referred to as vertices, and the connections between the vertices are termed as edges. Formally, a graph is a pair of sets (V, E), where V is a co
15+ min read
Add and Remove Edge in Adjacency List representation of a Graph Prerequisites: Graph and Its RepresentationIn this article, adding and removing edge is discussed in a given adjacency list representation. A vector has been used to implement the graph using adjacency list representation. It is used to store the adjacency lists of all the vertices. The vertex numbe
8 min read
Add and Remove Edge in Adjacency Matrix representation of a Graph Prerequisites: Graph and its representationsGiven an adjacency matrix g[][] of a graph consisting of N vertices, the task is to modify the matrix after insertion of all edges[] and removal of edge between vertices (X, Y). In an adjacency matrix, if an edge exists between vertices i and j of the grap
13 min read
Convert Adjacency Matrix to Adjacency List representation of Graph Prerequisite: Graph and its representations Given a adjacency matrix representation of a Graph. The task is to convert the given Adjacency Matrix to Adjacency List representation. Examples: Input: arr[][] = [ [0, 0, 1], [0, 0, 1], [1, 1, 0] ] Output: The adjacency list is: 0 -> 2 1 -> 2 2 -
6 min read
Graph Representation using Adjacency Matrix in C A graph is a data structure having a set of vertices and a collection of edges that each connect a pair of vertices. There are several ways to represent a graph in computer memory, and one of them is using an adjacency matrix. An adjacency matrix is a 2D array with one row per vertex and one column
4 min read
Prim’s MST for Adjacency List Representation | Greedy Algo-6 We recommend reading the following two posts as a prerequisite to this post. Greedy Algorithms | Set 5 (Prim’s Minimum Spanning Tree (MST)) Graph and its representationsWe have discussed Prim's algorithm and its implementation for adjacency matrix representation of graphs. The time complexity for th
15+ min read