1+ 今天开始继续贪心题目系列,让大家久等啦!
2+
3+ # 134. 加油站
4+
5+ 题目链接:https://leetcode-cn.com/problems/gas-station/
6+
7+ 在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[ i] 升。
8+
9+ 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[ i] 升。你从其中的一个加油站出发,开始时油箱为空。
10+
11+ 如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
12+
13+ 说明:
14+
15+ * 如果题目有解,该答案即为唯一答案。
16+ * 输入数组均为非空数组,且长度相同。
17+ * 输入数组中的元素均为非负数。
18+
19+ 示例 1:
20+ 输入:
21+ gas = [ 1,2,3,4,5]
22+ cost = [ 3,4,5,1,2]
23+
24+ 输出: 3
25+ 解释:
26+ 从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
27+ 开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
28+ 开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
29+ 开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
30+ 开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
31+ 开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
32+ 因此,3 可为起始索引。
33+
34+ 示例 2:
35+ 输入:
36+ gas = [ 2,3,4]
37+ cost = [ 3,4,3]
38+
39+ 输出: -1
40+ 解释:
41+ 你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
42+ 我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
43+ 开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
44+ 开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
45+ 你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
46+ 因此,无论怎样,你都不可能绕环路行驶一周。
147
248# 思路
349
4- ## 方法一
50+ ## 暴力方法
551
6- 来看一下贪心主要贪在哪里:
52+ 暴力的方法很明显就是O(n^2)的,遍历每一个加油站为起点的情况,模拟一圈。
753
8- 1 . 如果gas的总和小于cost总和,那么无论从哪里出发,一定是跑不了一圈的
9- 2 . remain[ i] = gas[ i] -cost[ i] 为一天剩下的油,remain[ i] ,i从0开始计算累加到最后一站,如果累加没有出现负数,说明从0出发,油就没有断过,那么0就是起点。
54+ 如果跑了一圈,中途没有断油,而且最后油量大于等于0,说明这个起点是ok的。
1055
11- 3 . 如果累加的最小值是负数,就要从非0节点出发,从后向前,看哪个节点能这个负数填平。
56+ 暴力的方法思路比较简单,但代码写起来也不是很容易,关键是要模拟跑一圈的过程。
1257
13- 代码如下:
58+ ** for循环适合模拟从头到尾的遍历,而while循环适合模拟环形遍历,要善于使用while!**
59+
60+ C++代码如下:
1461
1562```
1663class Solution {
64+ public:
65+ int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
66+ for (int i = 0; i < cost.size(); i++) {
67+ int rest = gas[i] - cost[i]; // 记录剩余油量
68+ int index = (i + 1) % cost.size();
69+ while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈
70+ rest += gas[index] - cost[index];
71+ index = (index + 1) % cost.size();
72+ }
73+ // 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置
74+ if (rest >= 0 && index == i) return i;
75+ }
76+ return -1;
77+ }
78+ };
79+ ```
80+ * 时间复杂度O(n^2)
81+ * 空间复杂度O(n)
82+
83+ C++暴力解法在leetcode上提交也可以过。
84+
85+ ## 贪心算法(方法一)
86+
87+ 直接从全局进行贪心选择,情况如下:
88+
89+ * 情况一:如果gas的总和小于cost总和,那么无论从哪里出发,一定是跑不了一圈的
90+ * 情况二:rest[ i] = gas[ i] -cost[ i] 为一天剩下的油,i从0开始计算累加到最后一站,如果累加没有出现负数,说明从0出发,油就没有断过,那么0就是起点。
91+
92+ * 情况三:如果累加的最小值是负数,汽车就要从非0节点出发,从后向前,看哪个节点能这个负数填平,能把这个负数填平的节点就是出发节点。
93+
94+ C++代码如下:
95+
96+ ``` C++
97+ class Solution {
1798public:
1899 int canCompleteCircuit(vector<int >& gas, vector<int >& cost) {
19100 int curSum = 0;
20- int min = INT_MAX; // 从起点出发,油箱里的油量
101+ int min = INT_MAX; // 从起点出发,油箱里的油量最小值
21102 for (int i = 0; i < gas.size(); i++) {
22- int remain = gas[i] - cost[i];
23- curSum += remain ;
103+ int rest = gas[ i] - cost[ i] ;
104+ curSum += rest ;
24105 if (curSum < min) {
25106 min = curSum;
26107 }
@@ -29,8 +110,8 @@ public:
29110 if (min >= 0) return 0; // 情况2
30111 // 情况3
31112 for (int i = gas.size() - 1; i >= 0; i--) {
32- int remain = gas[i] - cost[i];
33- min += remain ;
113+ int rest = gas[ i] - cost[ i] ;
114+ min += rest ;
34115 if (min >= 0) {
35116 return i;
36117 }
@@ -39,27 +120,41 @@ public:
39120 }
40121};
41122```
42- 其实这份代码还是比较复杂的。
123+ * 时间复杂度:O(n)
124+ * 空间复杂度:O(1)
125+
126+ **其实我不认为这种方式是贪心算法,因为没有找出局部最优,而是直接从全局最优的角度上思考问题**。
127+
128+ 但这种解法又说不出是什么方法,这就是一个从全局角度选取最优解的模拟操作。
43129
130+ 所以对于本解法是贪心,我持保留意见!
44131
45- ## 方法二
132+ 但不管怎么说,解法毕竟还是巧妙的,不用过于执着于其名字称呼。
46133
47- 换一个思路,首先如果总油量减去总消耗大于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量remain [ i ] 相加一定是大于零的。
134+ ## 贪心算法(方法二)
48135
49- 每个加油站的剩余量remain [ i ] 为gas [ i ] - cost [ i] 。
136+ 可以换一个思路,首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest [i]相加一定是大于等于零的 。
50137
51- i从0开始累加remain[ i] ,和记为curSum,如果curSum小于零,说明 [ 0, i] 区间都不能作为起始位置,起始位置从i+1算起。
138+ 每个加油站的剩余量rest[i]为gas[i] - cost[i]。
139+
140+ i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,起始位置从i+1算起,再从0计算curSum。
52141
53142如图:
54- < img src = ' ../pics/134.加油站.png ' width = 600 > </ img ></ div >
143+ 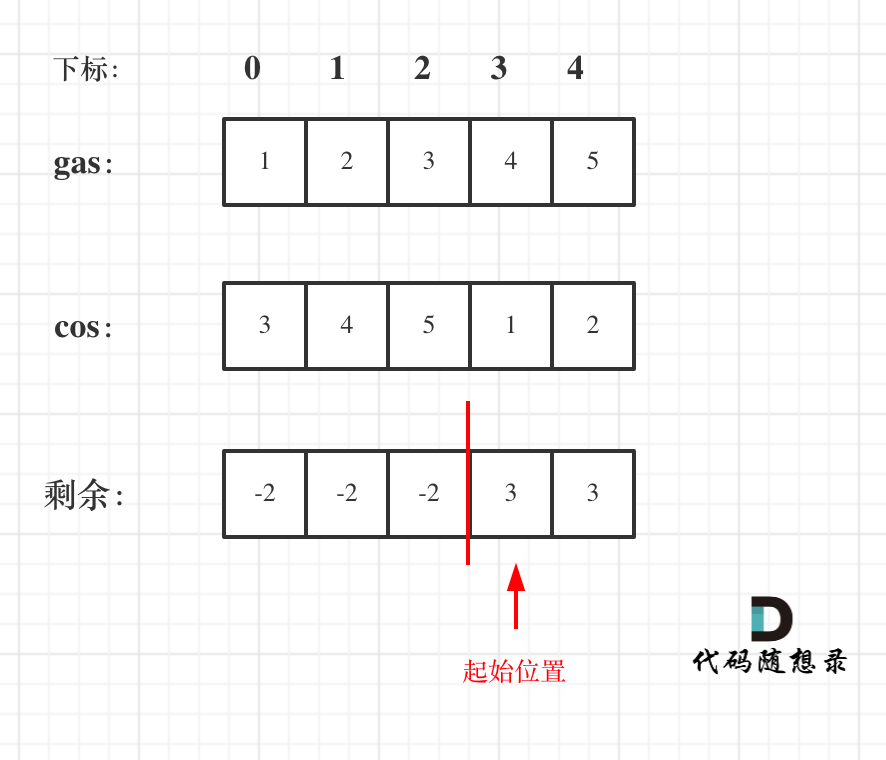
55144
56- 那么为什么 [ i,j] 区间和为负数,已经起始位置就可以是j +1呢,j+1后面就不会出现更大的负数?
145+ 那么为什么一旦 [i,j] 区间和为负数,起始位置就可以是j +1呢,j+1后面就不会出现更大的负数?
57146
58- 可以这么理解 j之前出现了多少负数,j后面就会出现多少正数,因为耗油总和是大于零的(前提我们已经确定了一定可以跑完全程)
147+ 如果出现更大的负数,就是更新j,那么起始位置又变成新的j+1了。
59148
60- 代码如下:
149+ 而且j之前出现了多少负数,j后面就会出现多少正数,因为耗油总和是大于零的(前提我们已经确定了一定可以跑完全程)。
61150
62- ```
151+ **那么局部最优:当前累加rest[j]的和curSum一旦小于0,起始位置至少要是j+1,因为从j开始一定不行。全局最优:找到可以跑一圈的起始位置**。
152+
153+ 局部最优可以推出全局最优,找不出反例,试试贪心!
154+
155+ C++代码如下:
156+
157+ ```C++
63158class Solution {
64159public:
65160 int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
@@ -69,20 +164,35 @@ public:
69164 for (int i = 0; i < gas.size(); i++) {
70165 curSum += gas[i] - cost[i];
71166 totalSum += gas[i] - cost[i];
72- if (curSum < 0) {
73- start = i + 1;
74- curSum = 0;
167+ if (curSum < 0) { // 当前累加rest[i]和 curSum一旦小于0
168+ start = i + 1; // 起始位置更新为i+1
169+ curSum = 0; // curSum从0开始
75170 }
76171 }
77172 if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了
78173 return start;
79174 }
80175};
81176```
177+ * 时间复杂度:O(n)
178+ * 空间复杂度:O(1)
179+
180+ ** 说这种解法为贪心算法,才是是有理有据的,因为全局最优解是根据局部最优推导出来的** 。
181+
182+ # 总结
183+
184+ 对于本题首先给出了暴力解法,暴力解法模拟跑一圈的过程其实比较考验代码技巧的,要对while使用的很熟练。
185+
186+ 然后给出了两种贪心算法,对于第一种贪心方法,其实我认为就是一种直接从全局选取最优的模拟操作,思路还是好巧妙的,值得学习一下。
187+
188+ 对于第二种贪心方法,才真正体现出贪心的精髓,用局部最优可以推出全局最优,进而求得起始位置。
189+
190+ 就酱,「代码随想录」值得推荐给身边每一位学习算法的同学朋友,很多录友关注后都感觉相见恨晚!
82191
83192
84193> **我是[程序员Carl](https:// github.com/youngyangyang04),[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png)可以找我,本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),关注后就会发现和「代码随想录」相见恨晚!**
85194
86195**如果感觉题解对你有帮助,不要吝啬给一个👍吧!**
87196
88197
198+
0 commit comments