The graph is a data structure that consists of vertices (or nodes) that can be connected to other vertices by edges.

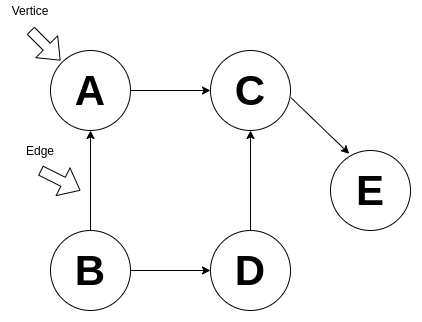
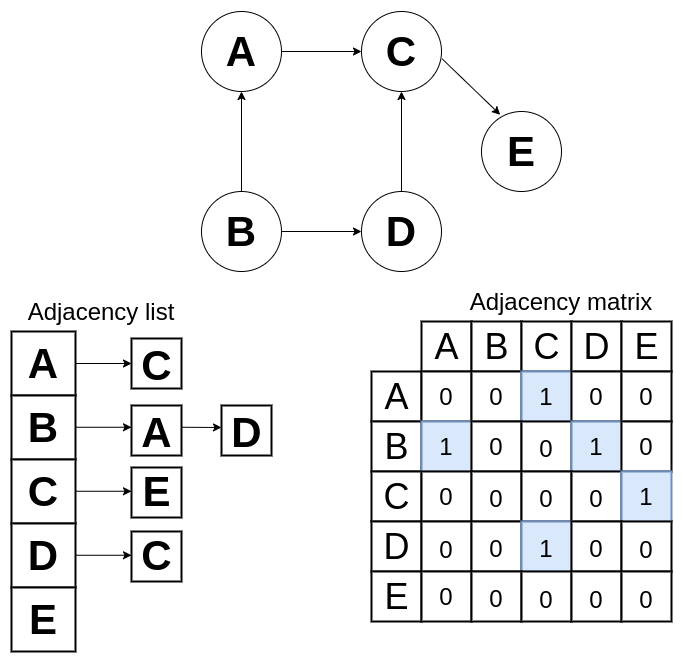
The degree is the number of edges that are connected to a vertex, for example, the vertex A has a degree of 1 and the vertex C has a degree of 2.

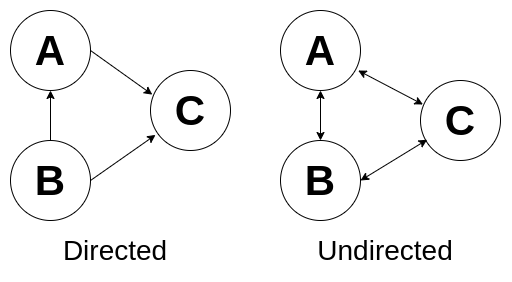
Graphs can either directed or undirected, directed graphs are like a one-way street, undirected is like a two-way street.

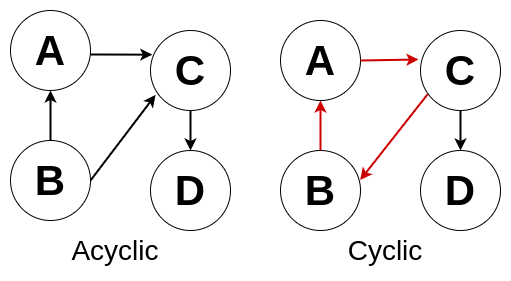
Graphs can also have cycles.

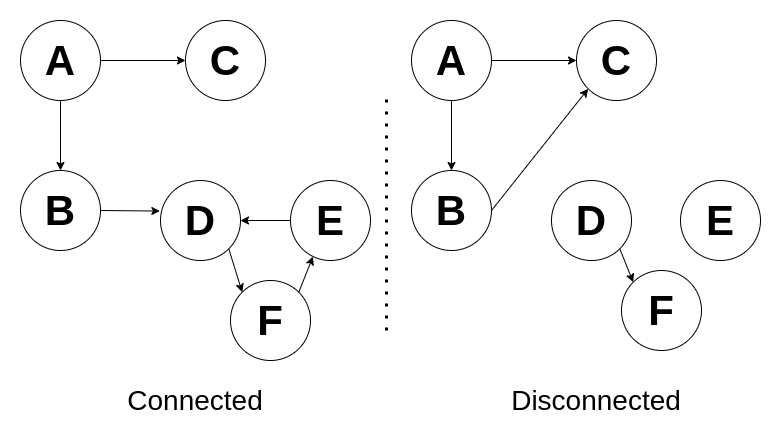
Graphs might be a disconnected one, that means it consists of isolated subgraphs, or a connected one, in which all every pair of nodes are connected by an edge.

Graphs can be used to represent networks, websites structure, also used in path optimization algorithms, there are applications in other fields, such as linguistics, physics, chemistry, biology, mathematics, etc.

Representation

Graphs can be represented with

• Adjacency list - Every node stores a list of adjacent vertices, for example, an array or that contains all vertices and each vertex contains another array with adjacent vertices, other data structures can be used instead of an array, like a hash table and a linked list.

• Adjacency matrix - An NxN boolean matrix (where N is the number of vertices), if the matrix[i][j] stores the value true, there is a connection between the vertices i and j. In an undirected graph matrix[j][i] also will store the value true. You can use other types instead of boolean, for example, numbers to represent weight.

Graph Search

Depth-first search

Depth-first search is a way to navigate a graph, it starts from a given vertex and visits each branch completely before moving to another branch. DFS is often used when we need to visit every node in the graph.

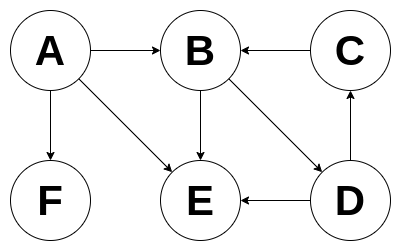
Using DPS on the graph above the nodes will be visited in the following order: A, B, D, C, E, F.

Breadth-first search

This is another way to navigate a graph, it starts from a given vertex and visits all adjacent vertices before go to any of their children. BFS is useful to find a path between two nodes.

Using DPS on the graph above the nodes will be visited in the following order: A, B, E, F, D, C.

Bidirectional search

Consists of running two breadth-first searches simultaneously, each one starts from a different vertex and runs until they collide. This is useful to find the shortest path between two vertices.

Heres an implementation of a directed graph using a adjacency list, because it will perform better in almost all operations:

1export class Node<T> { 2 data: T; 3 adjacent: Node<T>[]; 4 comparator: (a: T, b: T) => number; 5 6 constructor(data: T, comparator: (a: T, b: T) => number) { 7 this.data = data; 8 this.adjacent = []; 9 this.comparator = comparator; 10 } 11 12 addAdjacent(node: Node<T>): void { 13 this.adjacent.push(node); 14 } 15 16 removeAdjacent(data: T): Node<T> | null { 17 const index = this.adjacent.findIndex( 18 (node) => this.comparator(node.data, data) === 0 19 ); 20 21 if (index > -1) { 22 return this.adjacent.splice(index, 1)[0]; 23 } 24 25 return null; 26 } 27} 28 29class Graph<T> { 30 nodes: Map<T, Node<T>> = new Map(); 31 comparator: (a: T, b: T) => number; 32 33 constructor(comparator: (a: T, b: T) => number) { 34 this.comparator = comparator; 35 } 36 37 /** 38 * Add a new node if it was not added before 39 * 40 * @param {T} data 41 * @returns {Node<T>} 42 */ 43 addNode(data: T): Node<T> { 44 let node = this.nodes.get(data); 45 46 if (node) return node; 47 48 node = new Node(data, this.comparator); 49 this.nodes.set(data, node); 50 51 return node; 52 } 53 54 /** 55 * Remove a node, also remove it from other nodes adjacency list 56 * 57 * @param {T} data 58 * @returns {Node<T> | null} 59 */ 60 removeNode(data: T): Node<T> | null { 61 const nodeToRemove = this.nodes.get(data); 62 63 if (!nodeToRemove) return null; 64 65 this.nodes.forEach((node) => { 66 node.removeAdjacent(nodeToRemove.data); 67 }); 68 69 this.nodes.delete(data); 70 71 return nodeToRemove; 72 } 73 74 /** 75 * Create an edge between two nodes 76 * 77 * @param {T} source 78 * @param {T} destination 79 */ 80 addEdge(source: T, destination: T): void { 81 const sourceNode = this.addNode(source); 82 const destinationNode = this.addNode(destination); 83 84 sourceNode.addAdjacent(destinationNode); 85 } 86 87 /** 88 * Remove an edge between two nodes 89 * 90 * @param {T} source 91 * @param {T} destination 92 */ 93 removeEdge(source: T, destination: T): void { 94 const sourceNode = this.nodes.get(source); 95 const destinationNode = this.nodes.get(destination); 96 97 if (sourceNode && destinationNode) { 98 sourceNode.removeAdjacent(destination); 99 } 100 } 101 102 /** 103 * Depth-first search 104 * 105 * @param {T} data 106 * @param {Map<T, boolean>} visited 107 * @returns 108 */ 109 private depthFirstSearchAux(node: Node<T>, visited: Map<T, boolean>): void { 110 if (!node) return; 111 112 visited.set(node.data, true); 113 114 console.log(node.data); 115 116 node.adjacent.forEach((item) => { 117 if (!visited.has(item.data)) { 118 this.depthFirstSearchAux(item, visited); 119 } 120 }); 121 } 122 123 depthFirstSearch() { 124 const visited: Map<T, boolean> = new Map(); 125 this.nodes.forEach((node) => { 126 if (!visited.has(node.data)) { 127 this.depthFirstSearchAux(node, visited); 128 } 129 }); 130 } 131 132 /** 133 * Breadth-first search 134 * 135 * @param {T} data 136 * @returns 137 */ 138 private breadthFirstSearchAux(node: Node<T>, visited: Map<T, boolean>): void { 139 const queue: Queue<Node<T>> = new Queue(); 140 141 if (!node) return; 142 143 queue.add(node); 144 visited.set(node.data, true); 145 146 while (!queue.isEmpty()) { 147 node = queue.remove(); 148 149 if (!node) continue; 150 151 console.log(node.data); 152 153 node.adjacent.forEach((item) => { 154 if (!visited.has(item.data)) { 155 visited.set(item.data, true); 156 queue.add(item); 157 } 158 }); 159 } 160 } 161 162 breadthFirstSearch() { 163 const visited: Map<T, boolean> = new Map(); 164 this.nodes.forEach((node) => { 165 if (!visited.has(node.data)) { 166 this.breadthFirstSearchAux(node, visited); 167 } 168 }); 169 } 170} 171 172function comparator(a: number, b: number) { 173 if (a < b) return -1; 174 175 if (a > b) return 1; 176 177 return 0; 178} 179 180const graph = new Graph(comparator);