Basic Examples (3) 

Approximate a CauchyDistribution:

In[1]:=

Out[1]=

Approximate a CauchyDistribution using the specified starting point x₀, burn and thin values:

In[2]:=

Out[2]=

Approximate a MultivariateTDistribution in 2D:

In[3]:=

Out[3]=

Options (9) 

Method (1) 

The default Method is Automatic, in which case the jump function is a NormalDistribution (or MultinormalDistribution):

In[4]:=

Out[4]=

Scale (2) 

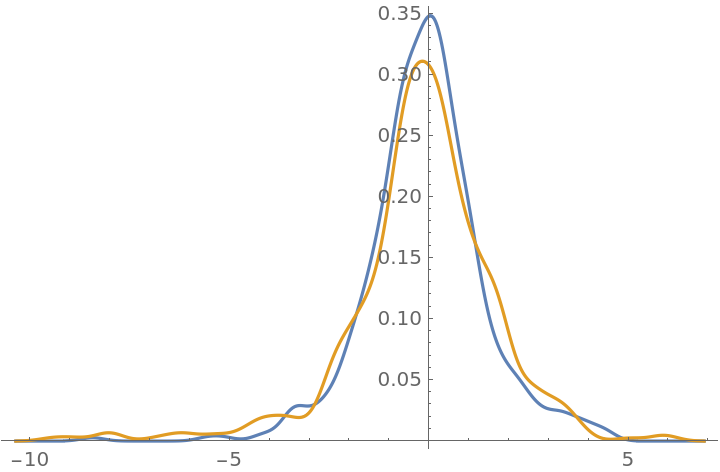
If f has multiple peaks, the algorithm can get stuck in the one nearest to the starting point:

In[5]:=

Out[5]=

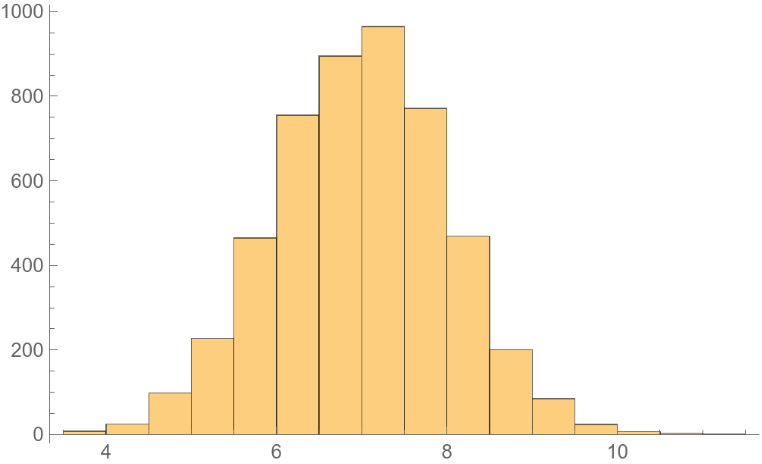
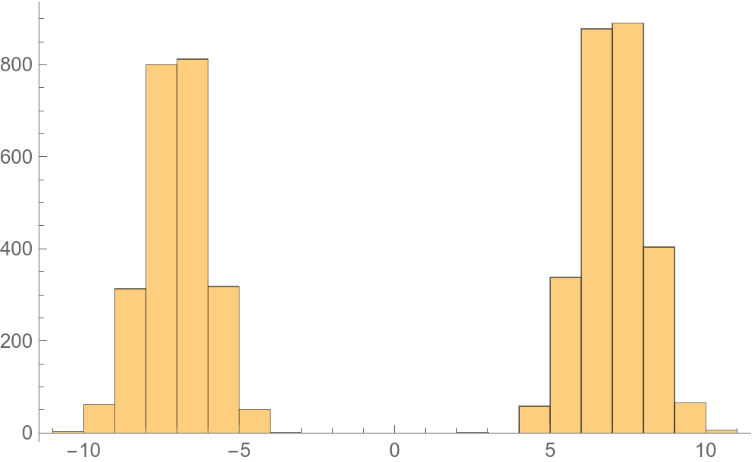
Use a larger "Scale" to explore the whole landscape:

In[6]:=

Out[6]=

JumpDistribution (2) 

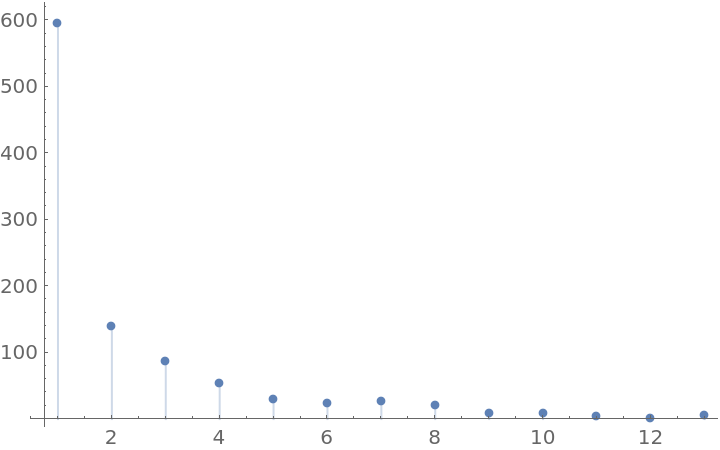
Use a discrete jump distribution to approximate discrete distributions:

In[7]:=

In[8]:=

In[9]:=

In[10]:=

Out[10]=

---

Multivariate example:

In[11]:=

Out[11]=

WorkingPrecision (1) 

Use WorkingPrecision to get higher precision in parameter estimates:

In[12]:=

Out[12]=

ShowRejectionRate (2) 

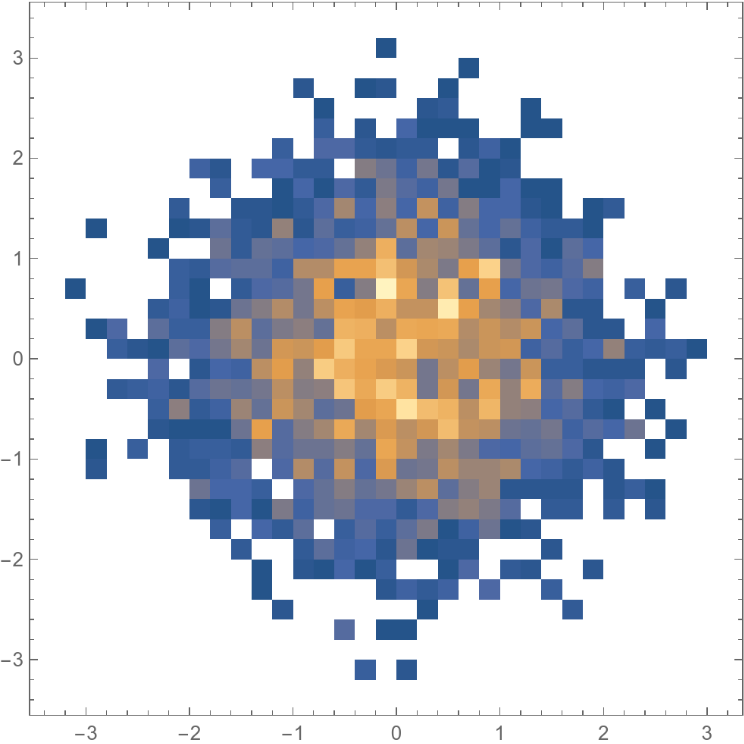
Use "ShowRejectionRate" to see the rejection rate of the process:

In[13]:=

Out[13]=

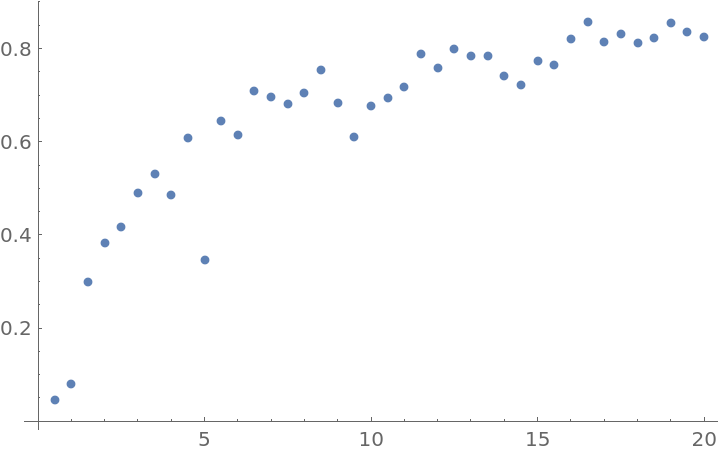
"ShowRejectionRate" can be used to select an optimal "Scale" for the method ("RejectionRate" is usually advised to be between 50% and 80% [see References]):

In[14]:=

Out[14]=

LogProbability (1) 

Use "LogProbability" to generate samples from a distribution defined by the Log of its PDF:

In[15]:=

Out[15]=

Applications (4) 

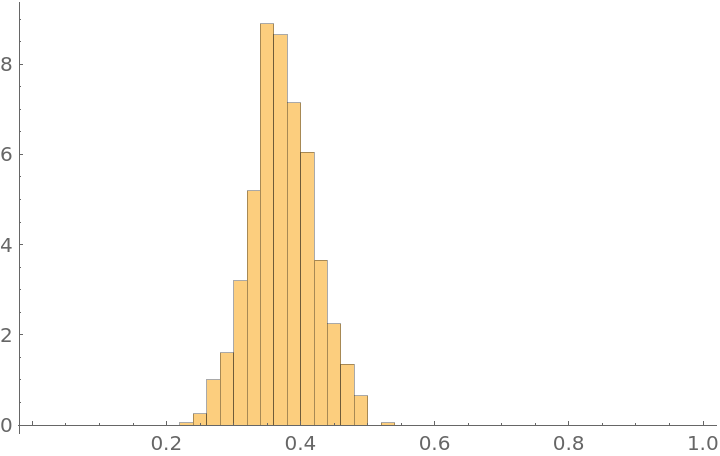
Generate sample data using BernoulliDistribution:

In[16]:=

Define a prior distribution for the parameter (in this case, the Jeffreys prior):

In[17]:=

Use Bayes's rule and multiply the Likelihood with the prior to get an f function, which is proportional to the posterior distribution of the parameter:

In[18]:=

Use MetropolisHastingsSequence to generate one thousand samples of the θ parameter and create a Histogram:

In[19]:=

Out[19]=

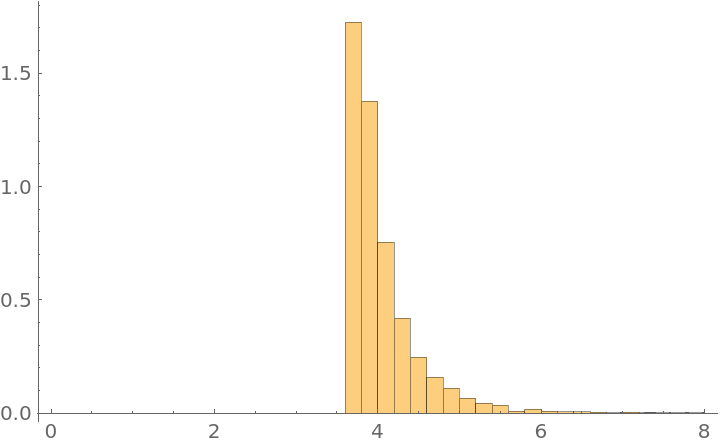
Infer the parameter of a UniformDistribution (also know as the German tank problem). First, generate a small sample of data using UniformDistribution:

In[20]:=

Define a prior distribution for the parameter (in this case, the non-normalizable Jeffreys prior):

In[21]:=

Use Bayes's rule and multiply the Likelihood with the prior to get a function that is proportional to the posterior distribution of the parameter:

In[22]:=

Use MetropolisHastingsSequence to generate one thousand samples of the θ parameter and generate a Histogram:

In[23]:=

Out[23]=

Generate sample data using NormalDistribution:

In[24]:=

Define a prior distribution for the parameter (in this case, the scale-free non-normalizable prior):

In[25]:=

Use Bayes's rule and multiply the Likelihood with the prior to get a function that is proportional to the posterior distribution of the parameter:

In[26]:=

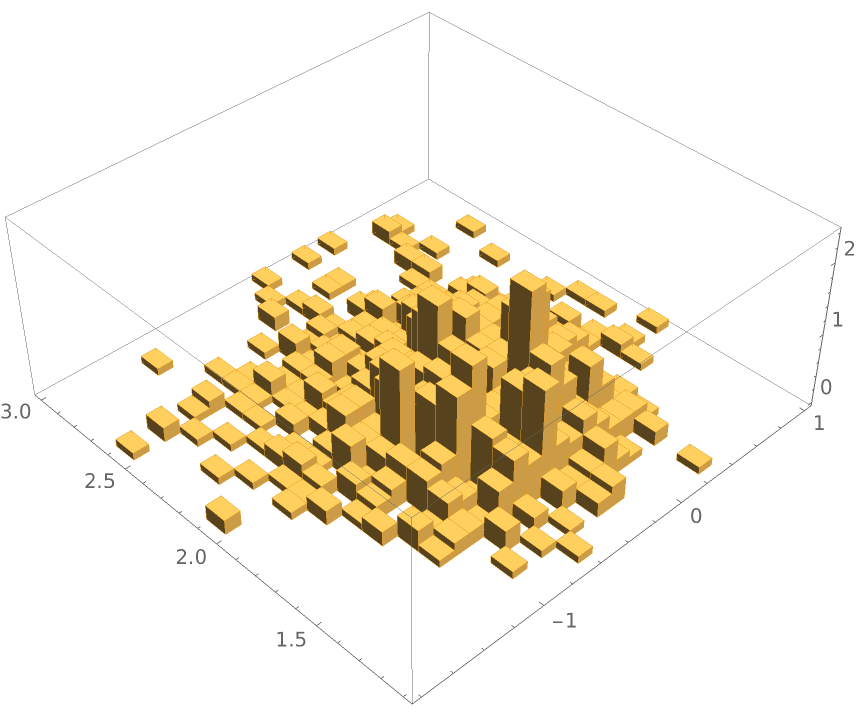
Use MetropolisHastingsSequence to generate one thousand samples of the {μ,σ} pair of parameters and generate a Histogram3D:

In[27]:=

Out[27]=

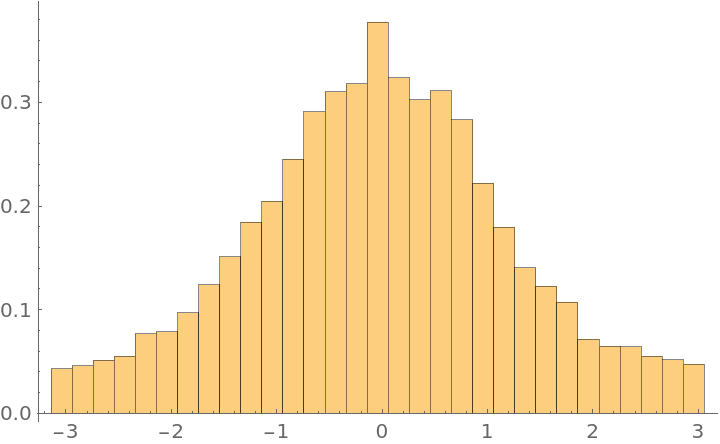
Generating a sample from distribution with PDF defined on a circle:

In[28]:=

Out[28]=

Properties and Relations (1) 

If f is normalized, it approximates RandomVariate[ProbabilityDistribution[f,{x,–∞,∞}],n]:

In[29]:=

Out[32]=

In[33]:=

Out[33]=

Possible Issues (2) 

The parameter thin should be an integer greater than 0:

In[34]:=

Out[34]=

The dimension of the parameter-dependent "JumpDistribution" must match the number of variables:

In[35]:=

Out[35]=