Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
List the possible cycle length counts of permutations of a given length
ResourceFunction["CycleLengthCountList"][n] returns a list of all possible cycle length counts that represent a partitioning of permutations of size n into disjoint cycles. |
Possible cycle length counts for 5-permutations:
| In[1]:= | |
| Out[1]= | 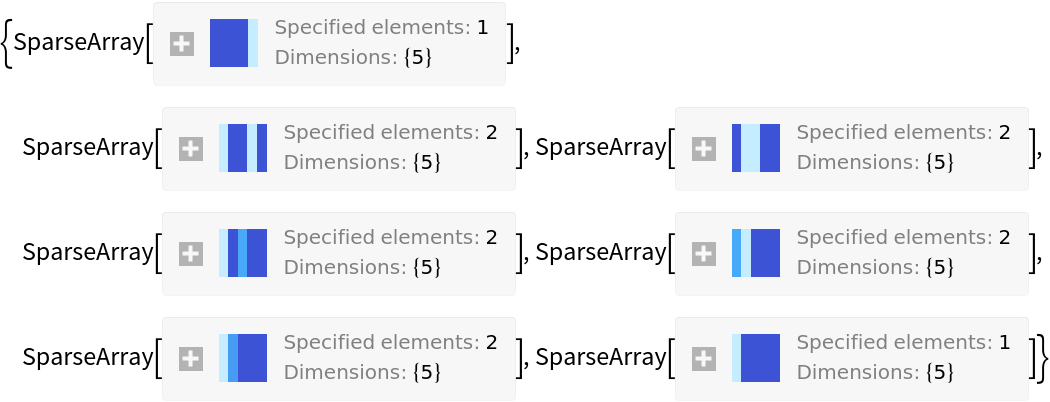 |
See the values:
| In[2]:= | |
| Out[2]= |  |
There are exactly as many cycle types of n-permutations as there are integer partitions of n:
| In[3]:= | |
| In[4]:= | |
| Out[4]= | |
Use the resource function PermutationCountByCycleLength to count the number of permutations of each possible type:
| In[5]:= | |
| In[6]:= | |
| Out[6]= | |
| In[7]:= | |
| Out[7]= | |
As expected, there are n! permutations in total:
| In[8]:= | |
| Out[8]= | |
| In[9]:= | |
| Out[9]= | |
Counting possible permutations of each type is the same as tallying cycle length counts in the Permutations list:
| In[10]:= | ![{#, ResourceFunction["PermutationCountByCycleLength"][#]} & /@ Sort[ResourceFunction["CycleLengthCountList"][n] // Normal]](https://www.wolframcloud.com/obj/resourcesystem/images/17d/17d25317-41e8-4540-ae46-1e3d06ab4bb0/5ec8b9fccb2dc086.png) |
| Out[10]= | |
| In[11]:= | |
| Out[11]= | |
| In[12]:= | |
| Out[12]= | |
This work is licensed under a Creative Commons Attribution 4.0 International License