Notes:
- For "regular" I intend maps in which the boundaries form a 3-regular planar graph
- For "different" I intend maps that cannot be topologically transformed one into another (faces have to be considered unnamed)
I've been looking for a formula, but it is too difficult for me. Maybe it has a simple solution but I don't see it.
This was my best guess, but I already know that it is not correct because full of symmetries, as it can be verified manually.
General formula:
- $$2\sum_{s_{(f-3)}=2f-5}^{2f-5+2} \text{...}\sum_{s_2=5}^{s_3} \sum_{s_1=3}^{s_2} s_1\left(s_1-1\right)\left(s_2-3\right)\text{...}\left(s_{(f-3)}-(2f-5-2)\right) $$
Examples:
- 4 faces = $$2\sum_{s_1=3}^5 s_1\left(s_1-1\right) $$
- 5 faces = $$2\sum_{s_2=5}^7 \sum_{s_1=3}^{s_2} s_1\left(s_1-1\right)\left(s_2-3\right)$$
Here are the first results that can be found manually (excluding symmetries):
- 2 faces = 0 possible regular map (an island and the ocean) (not to be counted, because not regular)
- 3 faces = 1 possible regular map (an island with two regions and the ocean) (two islands and the ocean wouldn't be regular)
- 4 faces = 3 possible regular maps (can be verified adding a face from the previous map)
- 5 faces =
20 possible regular maps(ERROR: There were duplicates) - 6 faces =
329 possible regular maps(ERROR: There were duplicates) - ...
These are all maps up to 5 faces (ERROR: contains duplicates):
maps http://4coloring.files.wordpress.com/2011/04/counting-maps-example-v3-named.png
Image for the comment on "triangulations of the sphere"
http://4coloring.files.wordpress.com/2011/04/counting-maps-duals-and-triangulations-v3.png
And without duplicates:
http://4coloring.files.wordpress.com/2011/04/counting-maps-example-v5.png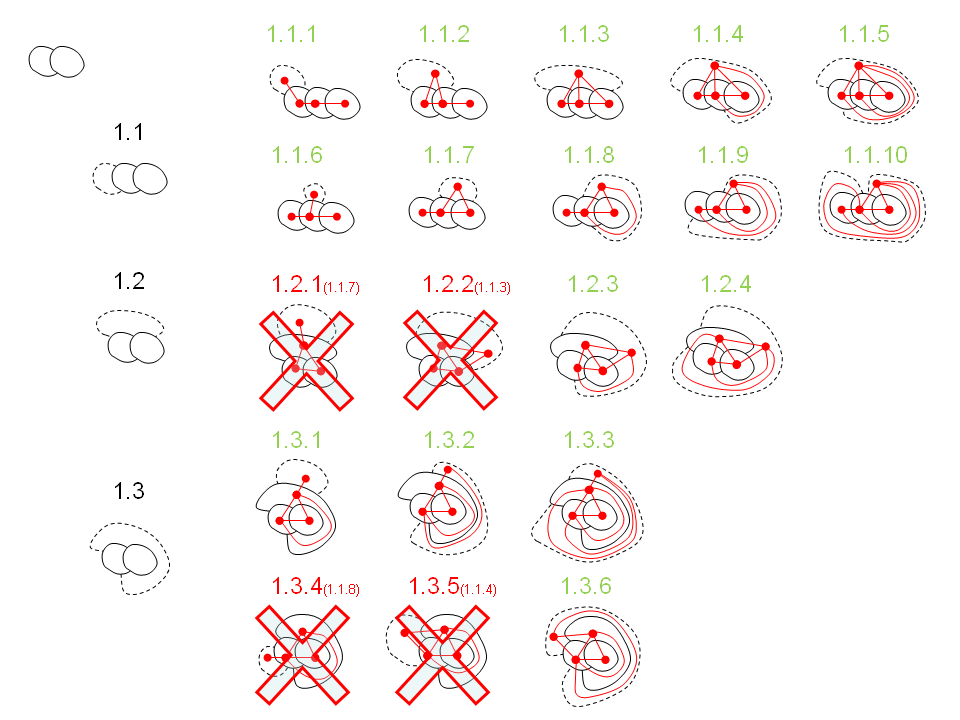
MODIFIED: 20/Apr/2011 - Removed "3-connected" from the question. See comment below.
MODIFIED: 21/Apr/2011 - Added a picture with all regular maps up to 5 faces
MODIFIED: 21/Apr/2011 - Added a picture for the comment on "triangulations of the sphere" and multiple edges, related to the dual graph of the original 3-regular planar graph
MODIFIED: 27/Apr/2011 - Manually computed number of different maps of 6 faces = 329, added numerical IDs to the maps
MODIFIED: 29/Apr/2011 - The manual computation of the number of regular maps contains some duplicated (Homeomorphic pairs)
MODIFIED: 29/Apr/2011 - Just to leave things a little more clean (I removed the duplicates ... I hope)
