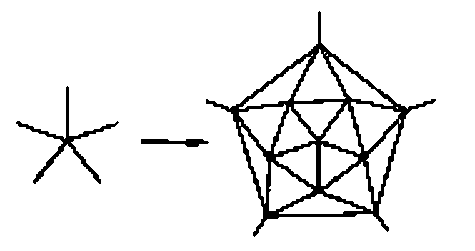
The answer is yes.
This construction is from the paper "Pairs of Hamiltonian circuits in 5-connected planar graphs" by Joseph Zaks. This is the "connected sum" of a 5-regular planar graph with an icosahedral graph.
Let $G$ be a 5-valent 5-connected planar graph and $v$ a vertex of it. Replace $v$ by the 11-vertex graph shown above. The new graph is 5-valent, 5-connected, planar and has 10 more vertices. Thus there is an infinitude of such graphs.