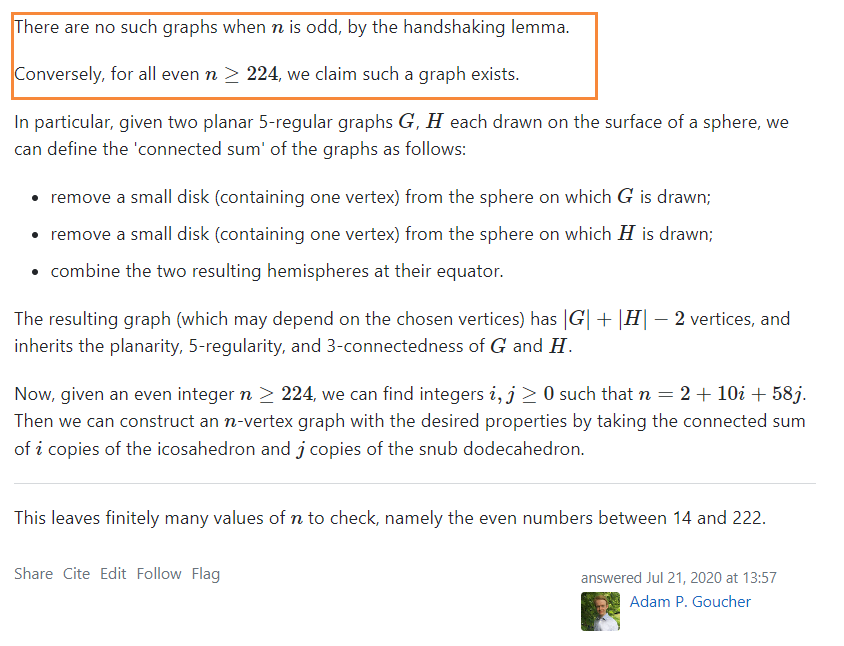
My question was partly inspired by the question linked below.
I see a wonderful construction of Adam P. Goucher, which guarantees that 3-connected 5-regular planar graphs are infinitely numerous. I wonder if there is also such a similar construct for the 5-connected 5-regular planar graphs. (Maybe I don't need to generate all of them like the title of this post.)
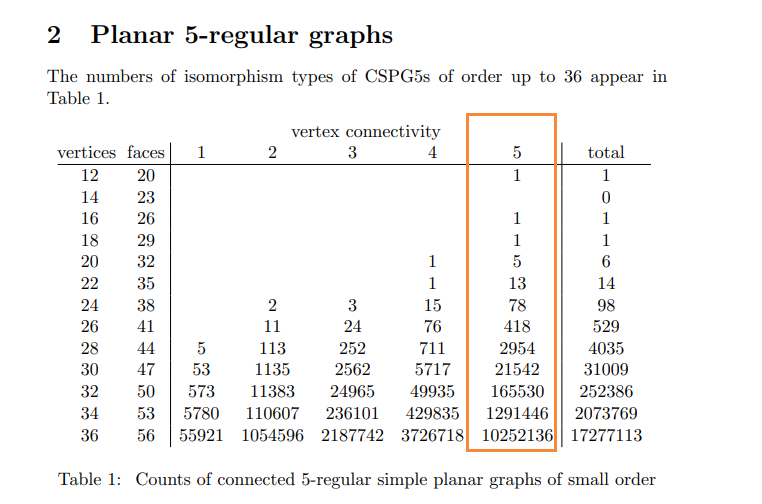
I noted the number of 5-connected 5-regular planar graphs with at most 36 vertices in the following paper.
- Hasheminezhad M, McKay B, Reeves T. Recursive generation of simple planar 5-regular graphs and pentangulations[J]. 2011.
Enough such graphs to convince me there are an unlimited number of such graphs. And when $n$ is large enough, for every $n$ there is a graph that I want.