I feel this may be a cut below some of the other amazingly deep theorems already mentioned, but I think a case can be made in favor of Steinitz's Theorem: the 1-skeletons (vertex-edge graphs) of convex polyhedra are exactly the 3-connected planar graphs. Steinitz's original proof also proved that any 3-connected graph can be realized with integer coordinates, a claim that is false in four dimensions: there exist fundamentally irrational 4-polytopes. Steinitz's proof requires integer coordinates with an exponential number of bits (exponential in $n$, the number of vertices), but the graph-drawing community has since lowered this to $O(n)$ bits.
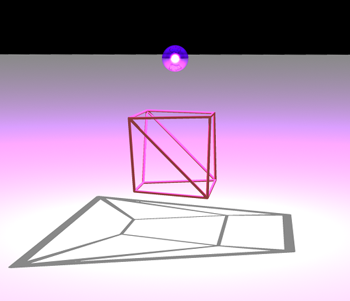
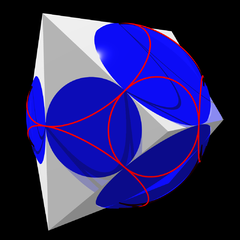
The Koebe-Andreev-Thurston Theorem shows that all these planar 3-connected graphs can be realized by very specialized convex polyhedra: those with a midsphere representationmidsphere representation:
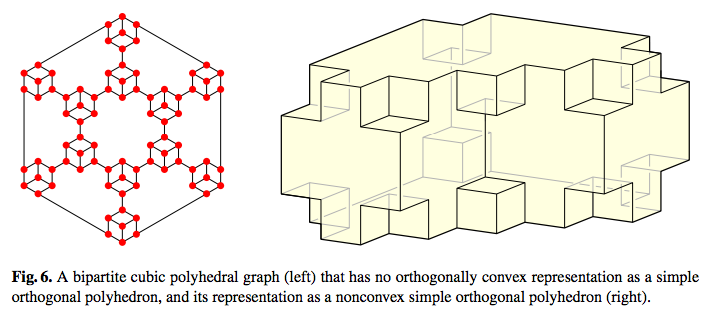
David Eppstein and Elena Mumford have extended Steinitz's theorem to orthogonal polyhedra:
Steinitz's 1922 Theorem is the source for much of the subsequent development of the connections between the geometry and the combinatorics of polytopes.
