Welcome to Subscribe On Youtube
1232. Check If It Is a Straight Line
Description
You are given an array coordinates, coordinates[i] = [x, y], where [x, y] represents the coordinate of a point. Check if these points make a straight line in the XY plane.
Example 1:
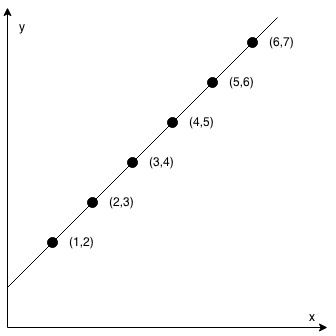
Input: coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]] Output: true
Example 2:
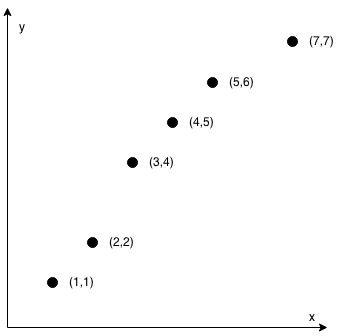
Input: coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]] Output: false
Constraints:
2 <= coordinates.length <= 1000coordinates[i].length == 2-10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4coordinatescontains no duplicate point.
Solutions
Solution 1: Mathematics
The time complexity is $O(n)$, where $n$ is the length of the coordinates array. The space complexity is $O(1)$.
-
class Solution { public boolean checkStraightLine(int[][] coordinates) { int x1 = coordinates[0][0], y1 = coordinates[0][1]; int x2 = coordinates[1][0], y2 = coordinates[1][1]; for (int i = 2; i < coordinates.length; ++i) { int x = coordinates[i][0], y = coordinates[i][1]; if ((x - x1) * (y2 - y1) != (y - y1) * (x2 - x1)) { return false; } } return true; } } -
class Solution { public: bool checkStraightLine(vector<vector<int>>& coordinates) { int x1 = coordinates[0][0], y1 = coordinates[0][1]; int x2 = coordinates[1][0], y2 = coordinates[1][1]; for (int i = 2; i < coordinates.size(); ++i) { int x = coordinates[i][0], y = coordinates[i][1]; if ((x - x1) * (y2 - y1) != (y - y1) * (x2 - x1)) { return false; } } return true; } }; -
class Solution: def checkStraightLine(self, coordinates: List[List[int]]) -> bool: x1, y1 = coordinates[0] x2, y2 = coordinates[1] for x, y in coordinates[2:]: if (x - x1) * (y2 - y1) != (y - y1) * (x2 - x1): return False return True -
func checkStraightLine(coordinates [][]int) bool { x1, y1 := coordinates[0][0], coordinates[0][1] x2, y2 := coordinates[1][0], coordinates[1][1] for i := 2; i < len(coordinates); i++ { x, y := coordinates[i][0], coordinates[i][1] if (x-x1)*(y2-y1) != (y-y1)*(x2-x1) { return false } } return true }