线性探查法的两个难点
原创
前文 哈希表核心原理 中我介绍了哈希表的核心原理和几个关键概念,其中提到了解决哈希冲突的方法主要有两种,分别是拉链法和线性探查法(也常叫做开放寻址法):
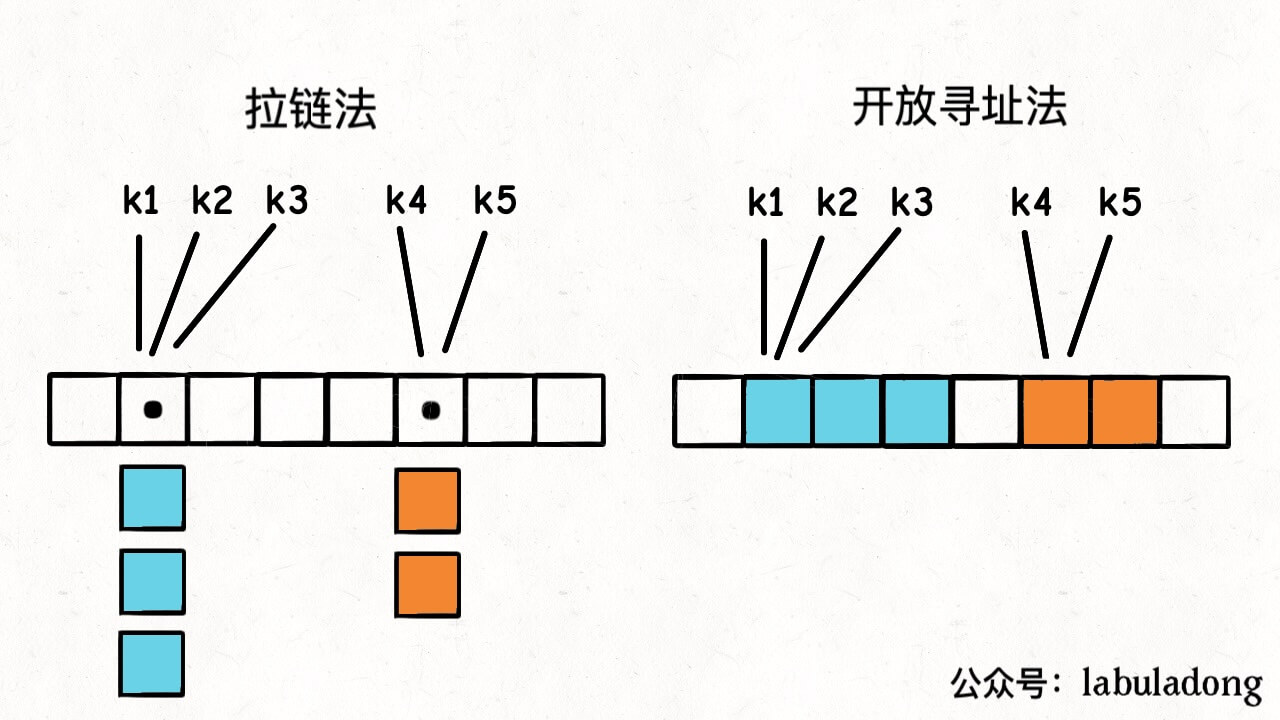
由于线性探查法稍微复杂一些,本文先讲解实现线性探查法的几个难点,下篇文章再给出具体的代码实现。
简化场景
之前介绍的拉链法应该是比较简单的,无非就是 table 中每个元素都是一个链表,出现哈希冲突的话往链表里塞元素就行了。
而线性探查法会更复杂,主要有两个难点,涉及到多种数组操作技巧。在讲清楚这两个难点之前,我们先设定一个简化的场景:
假设我们的哈希表只支持 key 类型为 int,value 类型为 int 的情况,且 table.length 固定为 10,hash 函数的实现是 hash(key) = key % 10。因为这样比较容易模拟出哈希冲突,比如 hash(1) 和 hash(11) 的值都是 1。
线性探查法的大致逻辑如下:
java
// 线性探查法的基本逻辑,伪码实现 class MyLinearProbingHashMap { // 数组中每个元素都存储一个键值对 private KVNode[] table = new KVNode[10]; private int hash(int key) { return key % table.length; } public void put(int key, int value) { int index = hash(key); KVNode node = table[index]; if (node == null) { table[index] = new KVNode(key, value); } else { // 线性探查法的逻辑 // 向后探查,直到找到 key 或者找到空位 while (index < table.length && table[index] != null && table[index].key != key) { index++; } table[index] = new KVNode(key, value); } } public int get(int key) { int index = hash(key); // 向后探查,直到找到 key 或者找到空位 while (index < table.length && table[index] != null && table[index].key != key) { index++; } if (table[index] == null) { return -1; } return table[index].value; } public void remove(int key) { int index = hash(key); // 向后探查,直到找到 key 或者找到空位 while (index < table.length && table[index] != null && table[index].key != key) { index++; } // 删除 table[index] // ... } }cpp
// 线性探查法的基本逻辑,伪码实现 class KVNode { public: int key; int value; KVNode(int k, int v) : key(k), value(v) {} }; class MyLinearProbingHashMap { private: // 数组中每个元素都存储一个键值对 KVNode* table[10] = {nullptr}; int hash(int key) { return key % 10; } public: // 析构函数 ~MyLinearProbingHashMap() { for (int i = 0; i < 10; i++) { if (table[i] != nullptr) { delete table[i]; table[i] = nullptr; } } } void put(int key, int value) { int index = hash(key); KVNode* node = table[index]; if (node == nullptr) { table[index] = new KVNode(key, value); } else { // 线性探查法的逻辑 // 向后探查,直到找到 key 或者找到空位 while (index < 10 && table[index] != nullptr && table[index]->key != key) { index++; } delete table[index]; table[index] = new KVNode(key, value); } } int get(int key) { int index = hash(key); // 向后探查,直到找到 key 或者找到空位 while (index < 10 && table[index] != nullptr && table[index]->key != key) { index++; } if (index >= 10 || table[index] == nullptr) { return -1; } return table[index]->value; } void remove(int key) { int index = hash(key); // 向后探查,直到找到 key 或者找到空位 while (index < 10 && table[index] != nullptr && table[index]->key != key) { index++; } // 删除 table[index] // ... } };python
# 线性探查法的基本逻辑,伪码实现 class KVNode: def __init__(self, key, value): self.key = key self.value = value class MyLinearProbingHashMap: # 数组中每个元素都存储一个键值对 def __init__(self): self.table = [None] * 10 def hash(self, key): return key % len(self.table) def put(self, key, value): index = self.hash(key) node = self.table[index] if node is None: self.table[index] = KVNode(key, value) else: # 线性探查法的逻辑 # 向后探查,直到找到 key 或者找到空位 while index < len(self.table) and self.table[index] is not None and self.table[index].key != key: index += 1 self.table[index] = KVNode(key, value) def get(self, key): index = self.hash(key) # 向后探查,直到找到 key 或者找到空位 while index < len(self.table) and self.table[index] is not None and self.table[index].key != key: index += 1 if self.table[index] is None: return -1 return self.table[index].value def remove(self, key): index = self.hash(key) # 向后探查,直到找到 key 或者找到空位 while index < len(self.table) and self.table[index] is not None and self.table[index].key != key: index += 1 # 删除 table[index] # ...go
// 线性探查法的基本逻辑,伪码实现 // 数组中每个元素都存储一个键值对 type KVNode struct { key int value int } type MyLinearProbingHashMap struct { table []*KVNode } func NewMyLinearProbingHashMap() *MyLinearProbingHashMap { return &MyLinearProbingHashMap{ table: make([]*KVNode, 10), } } func (m *MyLinearProbingHashMap) hash(key int) int { return key % len(m.table) } func (m *MyLinearProbingHashMap) Put(key int, value int) { index := m.hash(key) node := m.table[index] if node == nil { m.table[index] = &KVNode{key: key, value: value} } else { // 线性探查法的逻辑 // 向后探查,直到找到 key 或者找到空位 for index < len(m.table) && m.table[index] != nil && m.table[index].key != key { index++ } m.table[index] = &KVNode{key: key, value: value} } } func (m *MyLinearProbingHashMap) Get(key int) int { index := m.hash(key) // 向后探查,直到找到 key 或者找到空位 for index < len(m.table) && m.table[index] != nil && m.table[index].key != key { index++ } if m.table[index] == nil { return -1 } return m.table[index].value } func (m *MyLinearProbingHashMap) Remove(key int) { index := m.hash(key) // 向后探查,直到找到 key 或者找到空位 for index < len(m.table) && m.table[index] != nil && m.table[index].key != key { index++ } // 删除 table[index] // ... } func main() { hashMap := NewMyLinearProbingHashMap() hashMap.Put(1, 10) hashMap.Put(2, 20) fmt.Println(hashMap.Get(1)) // 10 fmt.Println(hashMap.Get(2)) // 20 fmt.Println(hashMap.Get(3)) // -1 hashMap.Put(2, 30) fmt.Println(hashMap.Get(2)) // 30 hashMap.Remove(2) fmt.Println(hashMap.Get(2)) // -1 }javascript
// 线性探查法的基本逻辑,伪码实现 class MyLinearProbingHashMap { constructor() { // 数组中每个元素都存储一个键值对 this.table = new Array(10).fill(null); } hash(key) { return key % this.table.length; } put(key, value) { var index = this.hash(key); var node = this.table[index]; if (node === null) { this.table[index] = { key: key, value: value }; } else { // 线性探查法的逻辑 // 向后探查,直到找到 key 或者找到空位 while (index < this.table.length && this.table[index] !== null && this.table[index].key !== key) { index++; } this.table[index] = { key: key, value: value }; } } get(key) { var index = this.hash(key); // 向后探查,直到找到 key 或者找到空位 while (index < this.table.length && this.table[index] !== null && this.table[index].key !== key) { index++; } if (this.table[index] === null) { return -1; } return this.table[index].value; } remove(key) { var index = this.hash(key); // 向后探查,直到找到 key 或者找到空位 while (index < this.table.length && this.table[index] !== null && this.table[index].key !== key) { index++; } // 删除 this.table[index] // ... } }基于这个假设场景,我们来看看线性探查法的两个难点。