@@ -80,15 +80,15 @@ function backtrack(solution, candidates): //入参可以理解为 路径, 选
8080
8181> 无论是排列、组合还是子集问题,简单说无非就是让你从序列 ` nums ` 中以给定规则取若干元素,主要有以下几种变体:
8282>
83- > ** 形式一、 元素无重不可复选,即 ` nums ` 中的元素都是唯一的,每个元素最多只能被使用一次,这也是最基本的形式** 。
83+ > ** 元素无重不可复选,即 ` nums ` 中的元素都是唯一的,每个元素最多只能被使用一次,这也是最基本的形式** 。
8484>
8585> - 以组合为例,如果输入 ` nums = [2,3,6,7] ` ,和为 7 的组合应该只有 ` [7] ` 。
8686>
87- > ** 形式二、 元素可重不可复选,即 ` nums ` 中的元素可以存在重复,每个元素最多只能被使用一次** 。
87+ > ** 元素可重不可复选,即 ` nums ` 中的元素可以存在重复,每个元素最多只能被使用一次** 。
8888>
8989> - 以组合为例,如果输入 ` nums = [2,5,2,1,2] ` ,和为 7 的组合应该有两种 ` [2,2,2,1] ` 和 ` [5,2] ` 。
9090>
91- > ** 形式三、 元素无重可复选,即 ` nums ` 中的元素都是唯一的,每个元素可以被使用若干次** 。
91+ > ** 元素无重可复选,即 ` nums ` 中的元素都是唯一的,每个元素可以被使用若干次** 。
9292>
9393> - 以组合为例,如果输入 ` nums = [2,3,6,7] ` ,和为 7 的组合应该有两种 ` [2,2,3] ` 和 ` [7] ` 。
9494>
@@ -117,13 +117,27 @@ function backtrack(solution, candidates): //入参可以理解为 路径, 选
117117
118118思路:
119119
120+ **子集的特性**:
121+
122+ - 对于给定的数组 `[1, 2, 3]`,它的所有子集应该包括空集、单个元素的子集、两个元素的组合和完整数组。
123+ - 每个元素都有两种选择:要么加入子集,要么不加入子集。
124+
125+ **回溯算法**:
126+
127+ - 使用回溯的方式可以从空集开始,逐步添加元素来生成所有子集。
128+ - 从当前的元素出发,尝试包含它或者不包含它,然后递归地处理下一个元素。
129+
130+ 参数定义:
131+
120132- `res`:一个列表,存储最终的所有子集,类型是 `List<List<Integer>>`。
121133
122134- `track`:一个临时列表,记录当前路径(即当前递归中形成的子集)。
123135- `start`:当前递归要开始的位置(即考虑从哪个位置开始生成子集)。这个 `start` 是非常重要的,它确保了我们在递归时不会重复生成相同的子集。
124136
125137完成回溯树的遍历就收集了所有子集。
126138
139+ 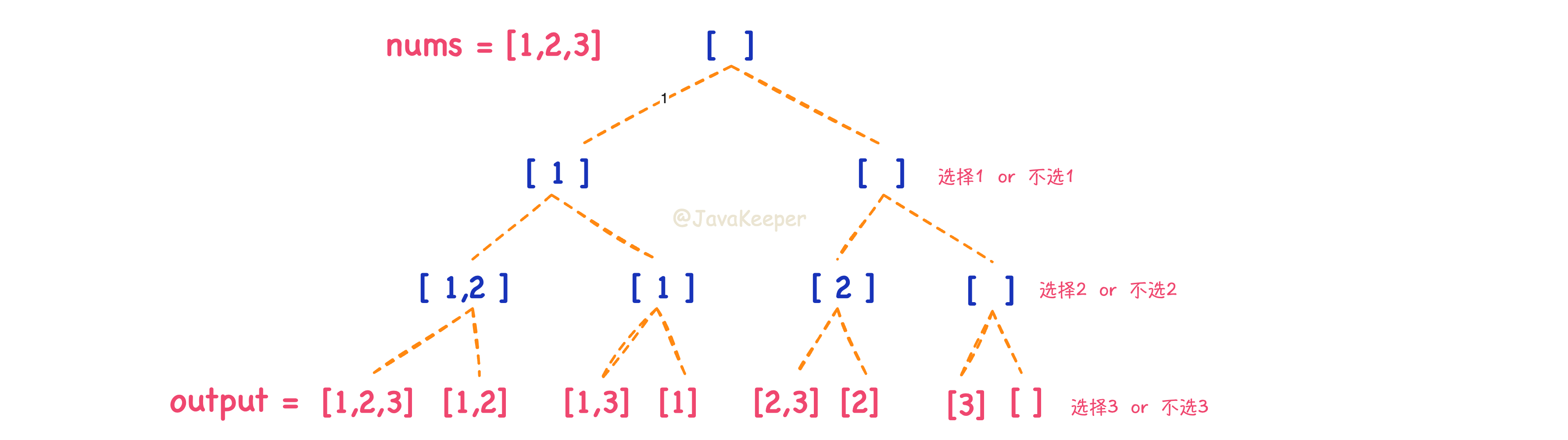
140+
127141```java
128142class Solution {
129143
@@ -175,11 +189,9 @@ class Solution {
175189> ]
176190> ```
177191
178- 思路:翻译一下就变成子集问题了:
192+ 思路:翻译一下就变成子集问题了:**给你输入一个数组 `nums = [1,2..,n]` 和一个正整数 `k`,请你生成所有大小为 `k` 的子集**。
179193
180- **给你输入一个数组 `nums = [1,2..,n]` 和一个正整数 `k`,请你生成所有大小为 `k` 的子集**。
181-
182- 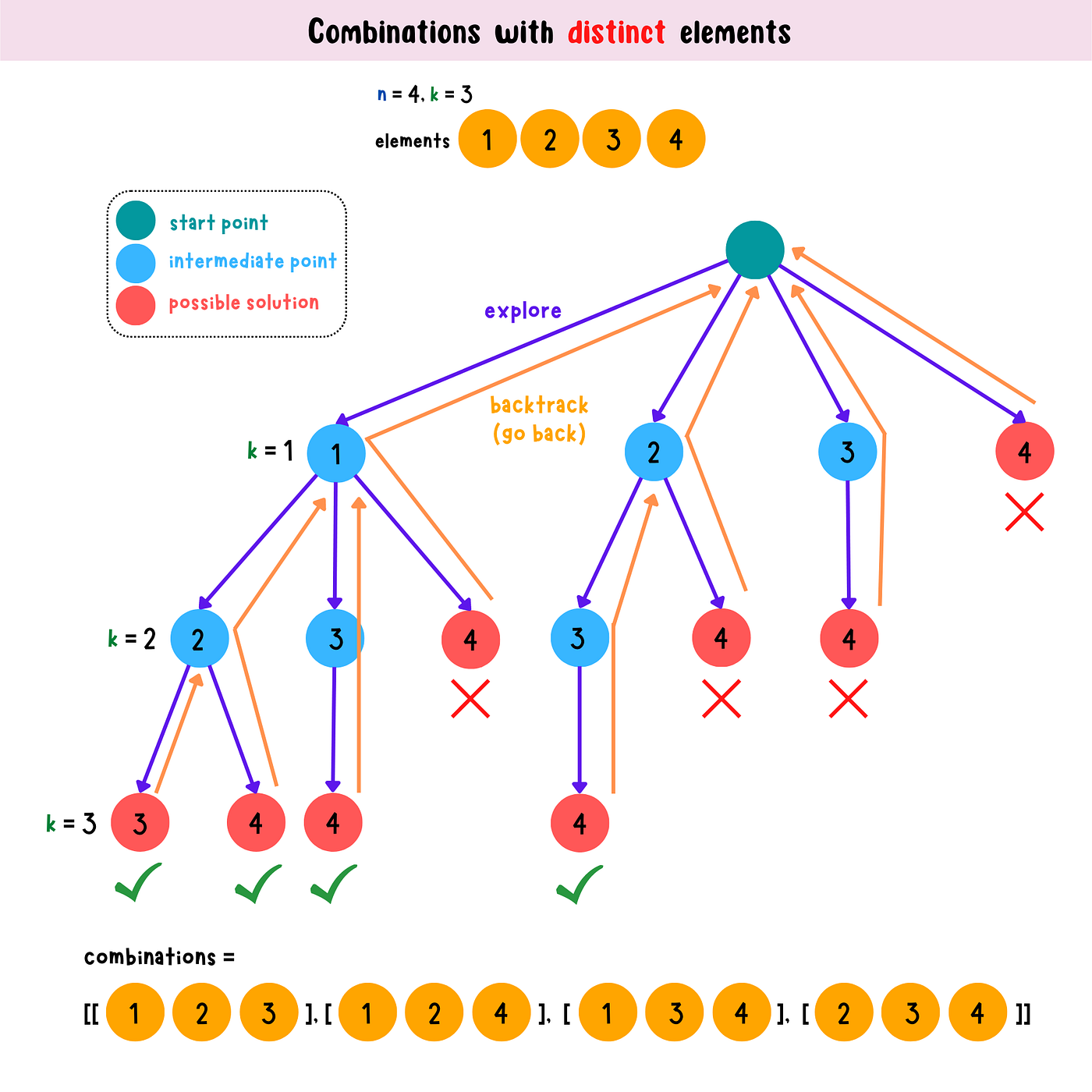
194+ 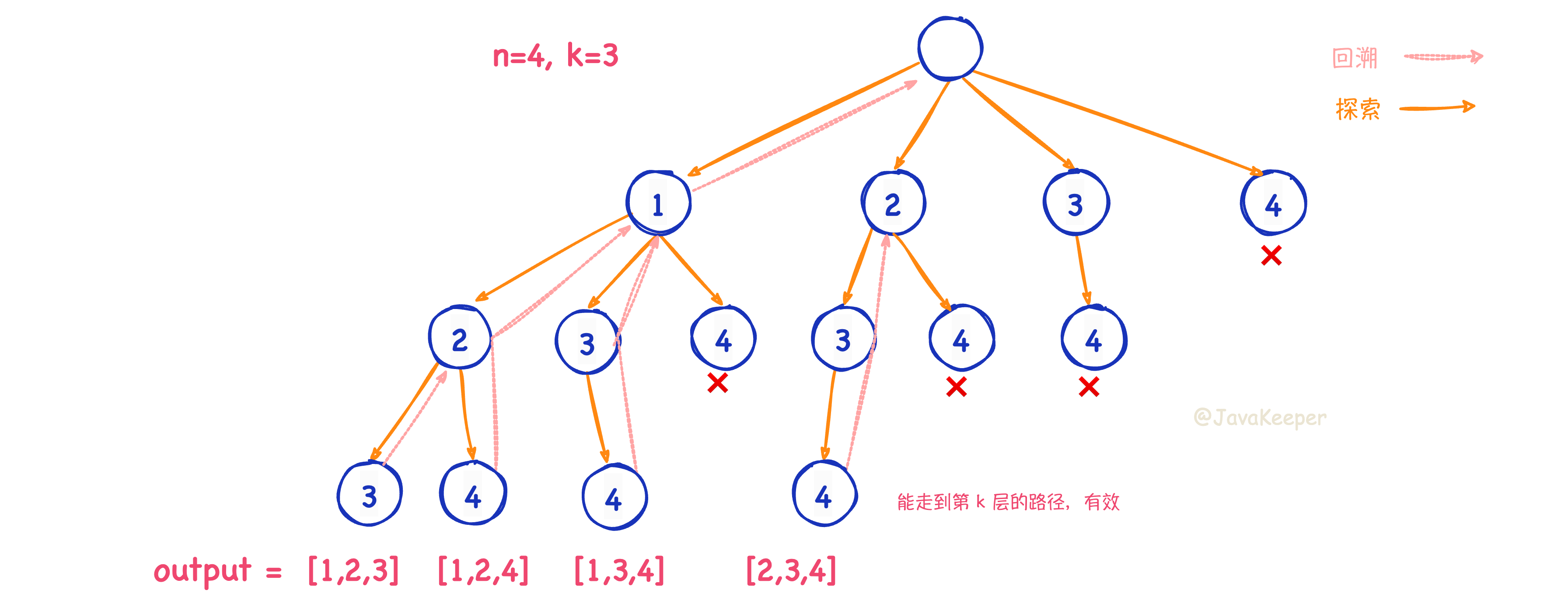
183195
184196反映到代码上,只需要稍改 base case,控制算法仅仅收集第 `k` 层节点的值即可:
185197
@@ -229,17 +241,17 @@ class Solution {
229241> 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
230242> ```
231243
232- 组合/子集问题使用 `start` 变量保证元素 `nums[start]` 之后只会出现 `nums[start+1..]`中的元素,通过固定元素的相对位置保证不出现重复的子集。
244+ 思路: 组合/子集问题使用 `start` 变量保证元素 `nums[start]` 之后只会出现 `nums[start+1..]`中的元素,通过固定元素的相对位置保证不出现重复的子集。
233245
234246**但排列问题本身就是让你穷举元素的位置,`nums[i]` 之后也可以出现 `nums[i]` 左边的元素,所以之前的那一套玩不转了,需要额外使用 `used` 数组来标记哪些元素还可以被选择**。
235247
236- 思路: 全排列共有 `n!` 个,我们可以按阶乘举例的思想,画出「回溯树」
248+ 全排列共有 `n!` 个,我们可以按阶乘举例的思想,画出「回溯树」
237249
238- 只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。**我们不妨把这棵树称为回溯算法的「决策树」**
250+ 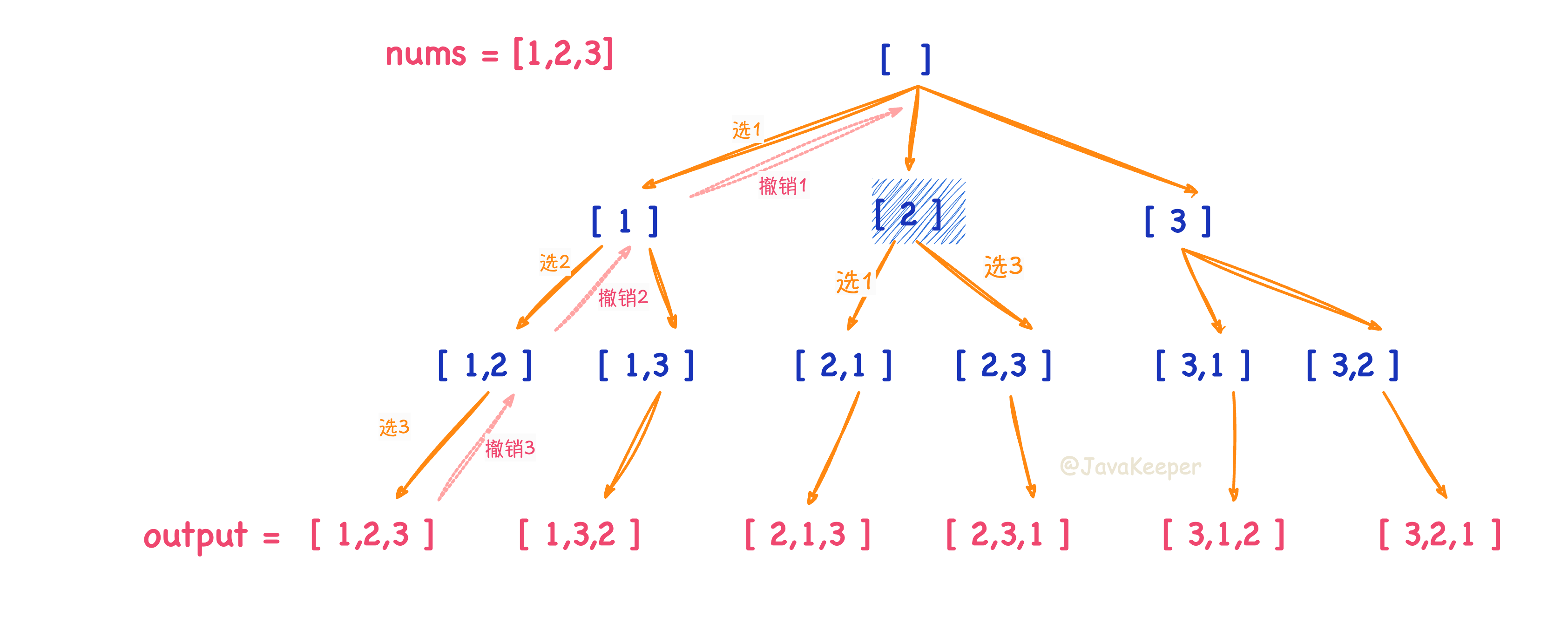
239251
240- **为啥说这是决策树呢,因为你在每个节点上其实都在做决策**。比如说你站在下图的红色节点上:你现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的 。
252+ > 回溯树是一种树状结构,树的每个节点表示一个状态(即当前的选择或部分解),树的每条边表示一次决策的选择。在回溯过程中,我们从根节点开始,递归地选择下一个数字,每次递归都相当于进入树的下一层 。
241253
242- **`[2]` 就是「路径」,记录你已经做过的选择;`[1,3]` 就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层叶子节点,这里也就是选择列表为空的时候**。
254+ > **东哥称为 决策树,你在每个节点上其实都在做决策**。因为比如你选了 2 之后,只能再选 1 或者 3,全排列是不允许重复使用数字的。 **`[2]` 就是「路径」,记录你已经做过的选择;`[1,3]` 就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层叶子节点,这里也就是选择列表为空的时候**。
243255
244256```java
245257class Solution {
@@ -287,8 +299,6 @@ class Solution {
287299}
288300```
289301
290- ![ image.png] ( https://pic.leetcode-cn.com/0bf18f9b86a2542d1f6aa8db6cc45475fce5aa329a07ca02a9357c2ead81eec1-image.png )
291-
292302
293303
294304### 二、元素可重不可复选
@@ -304,9 +314,7 @@ class Solution {
304314> 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
305315> ```
306316
307- 思路:按之前的思路,画出 回溯树,会有重复的,所有我们需要去重(剪枝),**体现在代码上,需要先进行排序,让相同的元素靠在一起,如果发现 `nums[i] == nums[i-1]`,则跳过**:
308-
309- 
317+ 思路:该问题的关键是**去重**(剪枝),**体现在代码上,需要先进行排序,让相同的元素靠在一起,如果发现 `nums[i] == nums[i-1]`,则跳过**
310318
311319```java
312320class Solution {
@@ -361,9 +369,11 @@ class Solution {
361369
362370思路:说这是一个组合问题,其实换个问法就变成子集问题了:请你计算 `candidates` 中所有和为 `target` 的子集。
363371
364- 只要额外用一个 `trackSum` 变量记录回溯路径上的元素和,然后将 base case 改一改即可解决这道题
372+ 1. **排序**:首先对 `candidates` 数组进行排序,排序后的数组方便处理重复数字。
373+ 2. **递归选择**:在递归过程中,确保如果当前数字和上一个数字相同,且上一个数字没有被选择过,则跳过当前数字,从而避免重复组合。
374+ 3. **递归终止条件**:如果 `target` 变为 0,表示找到了一个符合条件的组合;如果 `target` 小于 0,表示当前路径不合法,应该回溯。
365375
366- 
376+ 可以额外用一个 `trackSum` 变量记录回溯路径上的元素和,或者做减法,target == 0 递归结束也可以。
367377
368378```java
369379class Solution {
@@ -429,7 +439,19 @@ class Solution {
429439> [2,1,1]]
430440> ```
431441
432- 思路:
442+ 思路:典型的回溯
443+
444+ 1. **排序**:首先对 `nums` 进行排序。
445+
446+ 2. **回溯生成排列**:
447+
448+ - 递归生成排列时,每次递归时选择一个数字。
449+
450+ - 如果选择了当前数字,递归处理下一个数字。
451+
452+ - 每次递归前,判断是否跳过重复数字。
453+
454+ 3. **记录结果**:每当一个排列完成时,将其加入结果中。
433455
434456```java
435457class Solution {
@@ -495,8 +517,6 @@ class Solution {
495517
496518思路:**元素无重可复选,即 `nums` 中的元素都是唯一的,每个元素可以被使用若干次**,只要删掉去重逻辑即可
497519
498- 
499-
500520```java
501521class Solution {
502522
@@ -558,11 +578,13 @@ class Solution {
558578> 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
559579> ```
560580
561- 思路:
581+ 思路:回溯,递归地尝试每一位数字对应的所有字母,直到找出所有有效的组合
582+
583+ 首先,我们需要将每个数字 2 到 9 映射到其对应的字母
562584
563- 图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"] 。
585+ **递归终止条件**:当当前组合的长度与输入的数字字符串长度相同,就说明我们已经得到了一个有效的组合,可以将其加入结果集 。
564586
565- .jpg )
587+ 
566588
567589```java
568590class Solution {
@@ -574,6 +596,7 @@ class Solution {
574596 return result;
575597 }
576598
599+ //也可以用数组做映射
577600 Map<Character,String> digitToLetters = new HashMap<>();
578601 digitToLetters.put('2', "abc");
579602 digitToLetters.put('3', "def");
@@ -593,8 +616,10 @@ class Solution {
593616 result.add(track.toString());
594617 return;
595618 }
619+ // 获取当前数字对应的字母
596620 String letters = digitToLetters.get(digits.charAt(index));
597621 for (char letter : letters.toCharArray()) {
622+ //选择一个字母
598623 track.append(letter);
599624 backtrack(digits, index + 1, digitToLetters);
600625 track.deleteCharAt(track.length() - 1);
@@ -615,7 +640,9 @@ class Solution {
615640> 输出:["((()))","(()())","(())()","()(())","()()()"]
616641> ```
617642
618- 思路:
643+ 思路:
644+
645+ 
619646
620647```java
621648class Solution {
@@ -658,9 +685,7 @@ class Solution {
658685}
659686```
660687
661- dfs 思路:
662-
663- 由于一共要填 2n 个括号,那么当我们递归到终点时:
688+ dfs 思路:由于一共要填 2n 个括号,那么当我们递归到终点时:
664689
665690- 如果左括号少于 n 个,那么右括号也会少于 n 个,与 i == m 矛盾,因为每填一个括号 i 都会增加 1。
666691- 如果左括号超过 n 个,与 if open < n 矛盾,这行代码限制了左括号至多填 n 个。
@@ -815,3 +840,5 @@ class Solution {
815840## 参考与感谢:
816841
817842- https://yuminlee2.medium.com/combinations-and-combination-sum-3ed2accc8d12
843+ - https://medium.com/@sunshine990316/leetcode-python-backtracking-summary-medium-1-e8ae88839e85
844+ - https://blog.devgenius.io/10-daily-practice-problems-day-18-f7293b55224d
0 commit comments