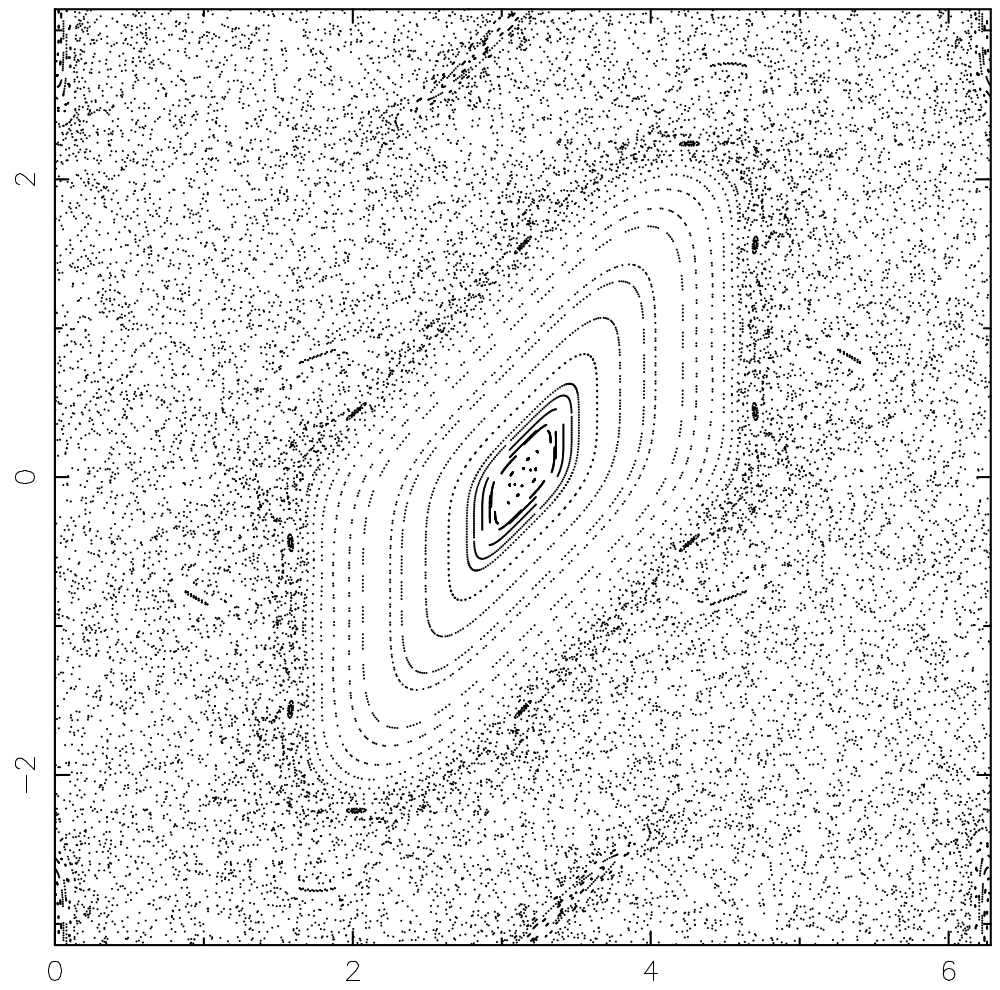TOPICS

Standard Map

DOWNLOAD Mathematica NotebookDownload Wolfram Notebook
StandardMap050
StandardMap100
StandardMap150
StandardMap200

A two-dimensional map also called the Taylor-Greene-Chirikov map in some of the older literature and defined by

I_(n+1)=I_n+Ksintheta_n
(1)
theta_(n+1)=theta_n+I_(n+1)
(2)
=I_n+theta_n+Ksintheta_n,
(3)

where I and theta are computed mod 2pi and K is a positive constant. Surfaces of section for various values of the constant K are illustrated above.

An analytic estimate of the width of the chaotic zone (Chirikov 1979) finds

deltaI=Be^(-AK^(-1/2)).
(4)

Numerical experiments give A approx 5.26 and B approx 240. The value of K at which global chaos occurs has been bounded by various authors. Greene's Method is the most accurate method so far devised.

authorboundexactapprox.
Hermann>1/(34)0.029411764
Celletti and Chierchia (1995)>(419)/(500)0.838
Greene approx -0.971635406
MacKay and Percival (1985)<(63)/(64)0.984375000
Mather<4/31.333333333

Fixed points are found by requiring that

I_(n+1)=I_n
(5)
theta_(n+1)=theta_n.
(6)

The first gives Ksintheta_n=0, so sintheta_n=0 and

theta_n=0,pi.
(7)

The second requirement gives

I_n+Ksintheta_n=I_n=0.
(8)

The fixed points are therefore (I,theta)=(0,0) and (0,pi). In order to perform a linear stability analysis, take differentials of the variables

dI_(n+1)=dI_n+Kcostheta_ndtheta_n
(9)
dtheta_(n+1)=dI_n+(1+Kcostheta_n)dtheta_n.
(10)

In matrix form,

[deltaI_(n+1); deltatheta_(n+1)]=[1 Kcostheta_n; 1 1+Kcostheta_n][deltaI_n; deltatheta_n].
(11)

The eigenvalues are found by solving the characteristic equation

|1-lambda Kcostheta_n; 1 1+Kcostheta_n-lambda|=0,
(12)

so

lambda^2-lambda(Kcostheta_n+2)+1=0
(13)
lambda_+/-=1/2[Kcostheta_n+2+/-sqrt((Kcostheta_n+2)^2-4)].
(14)

For the fixed point (0,pi),

lambda_+/-^((0,pi))=1/2[2-K+/-sqrt((2-K)^2-4)]
(15)
=1/2(2-K+/-sqrt(K^2-4K)).
(16)

The fixed point will be stable if |R(lambda^((0,pi)))|<2. Here, that means

1/2|2-K|<1
(17)
|2-K|<2
(18)
-2<2-K<2
(19)
-4<-K<0
(20)

so K in [0,4). For the fixed point (0, 0), the eigenvalues are

lambda_+/-^((0,0))=1/2[2+K+/-sqrt((K+2)^2-4)]
(21)
=1/2(2+K+/-sqrt(K^2+4K)).
(22)

If the map is unstable for the larger eigenvalue, it is unstable. Therefore, examine lambda_+^((0,0)). We have

1/2|2+K+sqrt(K^2+4K)|<1,
(23)

so

-2<2+K+sqrt(K^2+4K)<2
(24)
-4-K<sqrt(K^2+4K)<-K.
(25)

But K>0, so the second part of the inequality cannot be true. Therefore, the map is unstable at the fixed point (0, 0).

See also

Hénon-Heiles Equation

Explore with Wolfram|Alpha

References

Celletti, A. and Chierchia, L. "A Constructive Theory of Lagrangian Tori and Computer-Assisted Applications." Dynamics Rep. 4, 60-129, 1995.Chirikov, B. V. "A Universal Instability of Many-Dimensional Oscillator Systems." Phys. Rep. 52, 264-379, 1979.MacKay, R. S. and Percival, I. C. "Converse KAM: Theory and Practice." Comm. Math. Phys. 98, 469-512, 1985.Rasband, S. N. "The Standard Map." §8.5 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 11 and 178-179, 1990.Tabor, M. "The Hénon-Heiles Hamiltonian." §4.2.r in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 134-135, 1989.

Referenced on Wolfram|Alpha

Standard Map

Cite this as:

Weisstein, Eric W. "Standard Map." From MathWorld--A Wolfram Resource. https://mathworld.wolfram.com/StandardMap.html

Subject classifications