8
$\begingroup$

Question. Let $\mathcal{M}_3$ be the set of $3\times 3$ matrices with non-negative integer entries and unit determinant. What is the number of $M\in \mathcal{M}_3$ with fixed sum of entries? What is the answer if we allow only matrices with strictly positive entries?

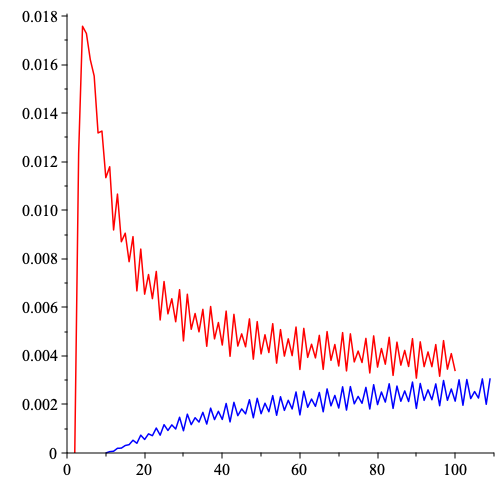
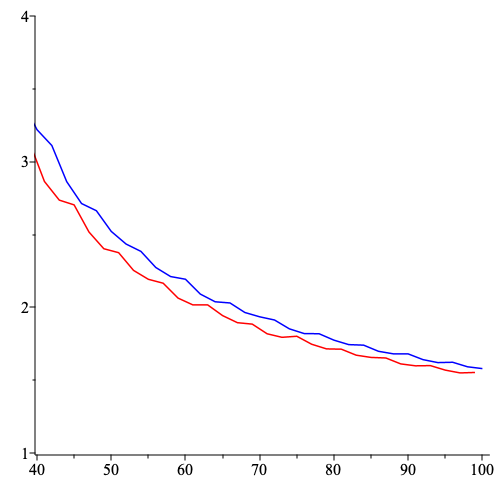
The rate of growth is also interesting. Below $n$ stands for the sum of entries.

Origin. For the similar question in the case of $2\times 2$ matrices we get $\phi(n)$ and $\phi(n) - 2$ respectively, see this recent post: Decomposition of a natural number as sum of positive integers.

Computation of the first elements. If we denote the answer sequence for non-negative case by $a_n$ then the first elements are

$n$ 1 2 3 4 5 6 7 8 9 10 11 12 13 14
$a_n$ 0 0 3 18 54 126 261 432 783 1134 1899 2286 3960 4680

$a = [0, 0, 0, 3, 18, 54, 126, 261, 432, 783, 1134, 1899, 2286, 3960, 4680, \ldots]$.

And if $b_n$ is the answer for the strictly positive case then $b_n = 0$ if $n \le 10$ and further we have

$n$ 11 12 13 14 15 16 17 18 19 20 21 22 23 24
$b_n$ 9 18 72 108 234 360 747 756 1818 1782 3222 3672 6615 5850

$b = [0,\ldots ,0, 9, 18, 72, 108, 234, 360, 747, 756, 1818, 1782, 3222, 3672, 6615, \ldots]$.

Unfortunately, both sequences do not seem to be in OEIS.

Thoughts on the growth. Evidently, $a_n\ge b_n$, and $a_n\le Cn^8$ because the number of partitions of $n$ into $9$ terms is $O(n^8)$. If we consider only upper-triangular matrices with ones on the diagonal, we will get the bound $a_n\ge Cn^2$.

Thus, the answer is of polynomial order. Note that this is different to the $2\times 2$ case where the number-theoretic properties played the main role.

Improve this question
$\endgroup$
14
  • 2
    $\begingroup$ You want the entries to be integers? $\endgroup$ Commented Feb 28, 2023 at 18:35
  • 1
    $\begingroup$ $n$ is much used but never defined. I take it $n$ stands for the sum of the entries? Should I be surprised that $b_n$ is not an increasing sequence? $\endgroup$ Commented Feb 28, 2023 at 22:24
  • 2
    $\begingroup$ The number of compositions of $n$ with 9 parts is $O(n^8)$. $\endgroup$ Commented Mar 1, 2023 at 0:11
  • 1
    $\begingroup$ And the number of upper triangular matrices with 1s on the diagonal and a composition of $n-3$ above the diagonal is not ${}\ge Cn^3$. It is $\Theta(n^2)$. Once you choose two of those entries, the third is forced. $\endgroup$ Commented Mar 1, 2023 at 0:56
  • 1
    $\begingroup$ @GerryMyerson, $n$ is a sum of entries, you are correct, it is now noted in the question. For $2\times 2$ matrices the answer is not increasing, so we can also expect it here. As you can see for other primes $p$ ($13, 17, 19$) $b_p$ is significantly larger than $b_{p - 1}$ and almost $b_{p + 1}$. The answer could be of the form $O(\phi(n)\cdot P(n))$ with some polynomial $P$ $\endgroup$ Commented Mar 1, 2023 at 7:15

2 Answers 2

Reset to default
4
$\begingroup$

(A comment rather than an answer.)

Here is a plot of $a_n/n^5$ (red) and $b_n/n^5$ (blue). It might not go far enough to show the asymptotic behaviour, but a possibility is that $a_n$ and $b_n$ are asymptotically the same and of order $\Theta(n^5)$.

enter image description here

Here is a plot of $a_n/b_n$ with odd $n$ in red and even $n$ in blue.

enter image description here

Values of $a_n$: 3, 18, 54, 126, 261, 432, 783, 1134, 1899, 2286, 3960, 4680, 6876, 8262, 12654, 12618, 20799, 20934, 30024, 32760, 48141, 43632, 68976, 68094, 91161, 93042, 138006, 112194, 187227, 170982, 224892, 226728, 310824, 265770, 418410, 372384, 484920, 455400, 677160, 520596, 839727, 726300, 905580, 900864, 1267065, 984474, 1528875, 1275318, 1680426, 1573398, 2227860, 1699722, 2558106, 2197980, 2829744, 2632266, 3709305, 2675448, 4336128, 3607416, 4446072, 4205142, 5623002, 4314492, 6752907, 5547510, 6989796, 6022962, 8947773, 6542532, 10176480, 8324190, 9964224, 9450396, 12778866, 9518256, 14843745, 11591730, 15006681, 13557816, 18773721, 13365792, 20262222, 17017884, 21061980, 18806256, 26303922, 18207054, 28574676, 23444388, 28962558, 26087202, 34559550, 25770906, 39755196, 31209228, 38935332, 33723702

Values of $b_n$: 9, 18, 72, 108, 234, 360, 747, 756, 1818, 1782, 3222, 3672, 6615, 5850, 11394, 11034, 16623, 17028, 30204, 22248, 45792, 39204, 56853, 57906, 87984, 72036, 128160, 108990, 154890, 141444, 236412, 167346, 306909, 253674, 334980, 332100, 503361, 369648, 636408, 505800, 707481, 646290, 988488, 712944, 1166760, 966708, 1306692, 1190376, 1797597, 1220004, 2150172, 1725192, 2204820, 2063214, 2893518, 2125296, 3564243, 2823642, 3708594, 3112686, 4920642, 3420018, 5671881, 4493988, 5531238, 5193000, 7316118, 5233482, 8656461, 6531660, 8762139, 7774002, 11231289, 7679628, 12234762, 10021086, 12747240, 11188980, 16320924, 10835082, 17876448, 14286942, 18103320, 16096968, 22026474, 15879564, 25652511, 19605996, 25073073, 21351708, 31695534, 21705012, 35093133, 27260136, 32296518, 30280140, 42823683, 29473992, 47349288

Improve this answer
$\endgroup$
2
  • $\begingroup$ I would very much appreciate it, if you could post the list of values. I wasn't able to compute that far $\endgroup$ Commented Mar 3, 2023 at 6:27
  • 1
    $\begingroup$ @PavelGubkin Done. These will become A361083 and A361082 soon. $\endgroup$ Commented Mar 3, 2023 at 8:13
3
$\begingroup$

$a_n$ is odd if and only if $n>1$ is a power of a prime $\equiv3\pmod4$. To see this, note that adding the constraints $M=M^T$ and $WMW=M$ for $W=\left(\begin{smallmatrix}&&1\\&1&\\1&&\end{smallmatrix}\right)$ does not change the parity of the number of solutions. With the added constraints you can work out the number exactly (it's always $0$, $2^{\omega(n)}$ or $2^{\omega(n)-1}$), and the only case that gives an odd number is $n=p^k$ with $p\equiv3\pmod4$.

Edit: $a_n-b_n$ is odd iff $n>1$ is of the form $2x^2\pm1$.

Improve this answer
$\endgroup$
2
  • $\begingroup$ The values of $n\le 89$ for which $b_n$ is odd are 11, 17, 23, 27, 33, 43, 47, 51, 59, 67, 73, 79, 81, 83. There are some non-prime-powers in there, can you make sense of it? $\endgroup$ Commented Mar 2, 2023 at 1:11
  • $\begingroup$ $b_{97}$ and $b_{99}$ are also odd. $\endgroup$ Commented Mar 2, 2023 at 2:44

You must log in to answer this question.

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.