There are multiple ways by which we can calculate the nth digit of pi by using Arctan formula and Bailey–Borwein–Plouffe formula.
Chudnovsky Algorithm is a fast way of calculating the digits of pi and is similar to the arctan's formula.This formula is derived from the Ramanujan’s π formulae.
Here's the Formula :-
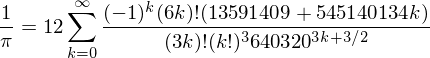
Simplifying further by solving the Fractional Power:
Dividing the series further into two parts a and b we get:
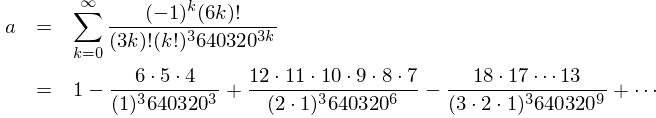
similarly,
we can calculate the next a term from the previous one, and the b terms from the a terms for simplifying the calculations.
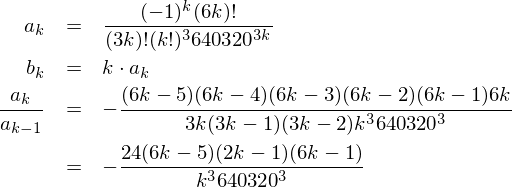
Implementing the formula using Python
import math def sqrt(n,m): m1=10**16 m2=float((n*m1)//m)/m1 b=(int(m1*math.sqrt(m2))*m)//m1 n_m=n*m while True: a=b b=(b+n_m//b)//2 if b==a: break return b def power(n): if n==0: return 1 r=power(n//2) if n%2==0: return r*r return r*r*10 def pi(): m = power(100000) c = (640320**3)//24 n = 1 Ak = m Asum = m Bsum = 0 while Ak != 0 : Ak *= -(6*n-5)*(2*n-1)*(6*n-1) Ak //= n*n*n*c Asum += Ak Bsum += n * Ak n = n + 1 result = (426880*sqrt(10005*m,m)*m)//(13591409*Asum+545140134*Bsum) return result stringPi = str(pi()) n = int(input()) print(stringPi[n-1]) This was the solution for GeeksForGeeks Problem.


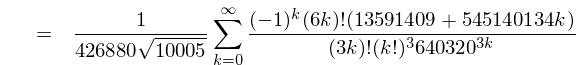

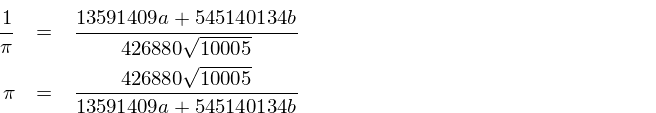

Top comments (0)